Plancksches Wirkungsquantum
Das Plancksche Wirkungsquantum oder die Planck Konstante spielt eine zentrale Rolle in der Quantenmechanik. Wenn du wissen möchtest, welche das ist, kannst du hier alles Wichtige dazu erfahren.
Am einfachsten geht das natürlich, indem du unser Video ansiehst. Darin habe wir das Thema nochmals aufgearbeitet und zusammengefasst.
Inhaltsübersicht
Plancksches Wirkungsquantum einfach erklärt
Das Plancksche Wirkungsquantum 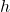 , oder auch Planck Konstante, ist eine Naturkonstante, die in der Quantenmechanik eine fundamentale Rolle spielt. Dort beschreibt sie für jedes harmonisch schwingende System (harmonischer Oszillator) das konstante Verhältnis von Frequenz und kleinstmöglicher zugehöriger Energie im System. Jede höhere Energie im Oszillator kann nur ein ganzzahliges Vielfaches dieser Grundzustandsenergie sein. Die Energie in solchen Systemen kann also nur diskrete Werte annehmen, sie ist gequantelt.
, oder auch Planck Konstante, ist eine Naturkonstante, die in der Quantenmechanik eine fundamentale Rolle spielt. Dort beschreibt sie für jedes harmonisch schwingende System (harmonischer Oszillator) das konstante Verhältnis von Frequenz und kleinstmöglicher zugehöriger Energie im System. Jede höhere Energie im Oszillator kann nur ein ganzzahliges Vielfaches dieser Grundzustandsenergie sein. Die Energie in solchen Systemen kann also nur diskrete Werte annehmen, sie ist gequantelt.
Zudem stellt das Plancksche Wirkungsquantum in der nicht-relativistischen Quantenmechanik gemäß dem Welle-Teilchen-Dualismus die Verbindung von Teilcheneigenschaften wie Energie und Impuls mit Welleneigenschaften wie Frequenz und Wellenlänge her.
Planck Konstante Zahlenwert
Das Plancksche Wirkungsquantum ist benannt nach Max Planck, der es im Zuge seiner Untersuchung der Schwarzkörperstrahlung einführte. Es tauchte erstmals in der von ihm entwickelten Planckschen Strahlungsgesetz für die Strahlungsleistung von Schwarzkörpern auf, mit dem sich diese Strahlungseistung für alle Wellenlängen korrekt beschreiben. Zudem stimmt das Plancksche Strahlungsgesetz für sehr große Wellenlängen mit dem Rayleigh-Jeans Gesetz und für sehr kleine Wellenlängen mit dem Wiensche Strahlungsgesetz überein. Diese Gesetze waren bereits vor Planck bekannt und wurden von ihm vereinigt.
Die Plancksche Konstante 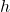 hat den definiert exakten Wert
hat den definiert exakten Wert
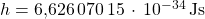
und seine Einheit ist Joule mal Sekunden, also Energie mal Zeit, die Einheit der Wirkung. Oft wird auch das sogenannte „reduzierte Plancksche Wirkungsquantum“ 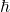 (sprich „h quer“) verwendet
(sprich „h quer“) verwendet
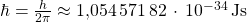 .
.
Plancksches Wirkungsquantum bei Photonen und Materiewellen
Durch den Photoeffekt
wissen wir, dass die Energie von Licht nicht kontinuierlich, sondern in diskreten Energieportionen übertragen wird. Die Energie von Licht ist also gequantelt. Diese Lichtquanten nennt man Photonen und ihre Energie 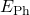 und ihr Impuls
und ihr Impuls 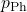 stehen über das Plancksche Wirkunsgquantum in Verbindung mit ihrer Wellenlänge
stehen über das Plancksche Wirkunsgquantum in Verbindung mit ihrer Wellenlänge 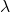 und ihrer Frequenz
und ihrer Frequenz 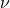 „nü“ (der Wellenlänge und Frequenz des Lichts)
„nü“ (der Wellenlänge und Frequenz des Lichts)
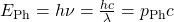 .
.
Oft wird die Frequenz auch  genannt, man merkt sich also am besten beide Formeln (E=h · f) und ( E = h · ν). Diese Relation für Photonenenergie und -impuls können wir auch mittels der Kreisfrequenz
genannt, man merkt sich also am besten beide Formeln (E=h · f) und ( E = h · ν). Diese Relation für Photonenenergie und -impuls können wir auch mittels der Kreisfrequenz 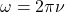 , der Wellenzahl
, der Wellenzahl
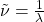 und der Kreiswellenzahl
und der Kreiswellenzahl 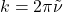 ausdrücken
ausdrücken
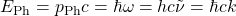 .
.
Für Materieteilchen finden wir gemäß dem Welle-Teilchen-Dualismus die de Broglie Wellenlänge
ihrer Materiewellen mit derselben Formel
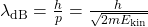 ,
,
wobei wir den Teilchenimpuls 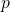 , wie hier für den nicht-relativistischen Fall, auch über die kinetische Energie
angeben können.
, wie hier für den nicht-relativistischen Fall, auch über die kinetische Energie
angeben können.
Plancksches Wirkungsquantum bestimmen
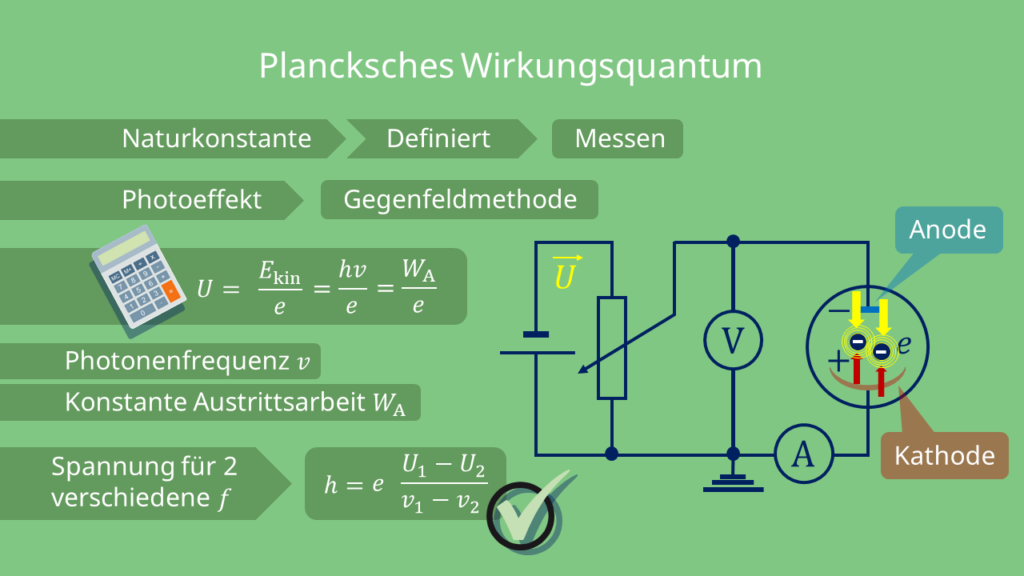
Eine einfache Methode zur Bestimmung des Planckschen Wirkungsquantums ist die Gegenfeldmethode beim Photoeffekt.
Dabei wird in einer Photozelle ein Metall (Kathode) mit Licht der Frequenz 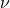 bestrahlt, sodass die auftreffenden Photonen Elektronen aus dem Metall herauslösen. Nach Abzug der konstanten Austrittsarbeit
bestrahlt, sodass die auftreffenden Photonen Elektronen aus dem Metall herauslösen. Nach Abzug der konstanten Austrittsarbeit 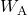 haben die Elektronen dann die kinetische Energie
haben die Elektronen dann die kinetische Energie
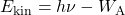 .
.
Die Elektronen bewegen sich dann zu einer (metallischen) Anode und werden dort absorbiert. Alles in allem messen wir einen Photostrom und eine Photospannung zwischen Kathode und Anode. Jetzt können wir eine äußere elektrische Spannung 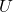 anlegen, die gegen die Photospannung wirkt und die Elektronen auf dem Weg zur Anode abbremst. Wenn der Photostrom verschwindet, haben wir
anlegen, die gegen die Photospannung wirkt und die Elektronen auf dem Weg zur Anode abbremst. Wenn der Photostrom verschwindet, haben wir 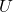 genau so eingestellt, dass es die Photospannung kompensiert und für die Elektronenenergie gilt
genau so eingestellt, dass es die Photospannung kompensiert und für die Elektronenenergie gilt
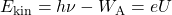 .
.
Ist die Elementarladung  bekannt (zum Beispiel aus dem Milikan-Versuch
), können wir so das Plancksche Wirkungsquantum bestimmen. Dazu bestimmen wir für einige Frequenzen
bekannt (zum Beispiel aus dem Milikan-Versuch
), können wir so das Plancksche Wirkungsquantum bestimmen. Dazu bestimmen wir für einige Frequenzen 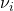 die jeweils benötigten Gegenspannungen
die jeweils benötigten Gegenspannungen 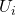 . Für die Differenz zweier Gegenspannungen
. Für die Differenz zweier Gegenspannungen 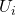 und
und 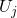 gilt gemäß obiger Gleichung
gilt gemäß obiger Gleichung
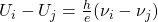 .
.
Wenn wir jetzt einige solche Spannungsdifferenzen über ihren zugehörigen Frequenzdifferenzen auftragen, finden wir eine Gerade, deren Steigung 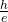 wir messen und so die Planck Konstante bestimmen können.
wir messen und so die Planck Konstante bestimmen können.
Planck Konstante und die Unschärferelation
Im Gegensatz zur klassischen Physik ist es in der Quantenmechanik möglich, dass verschiedene Messgrößen, sogenannte „Observablen“, nicht unabhängig voneinander messbar sind. Bei solchen miteinander unverträglichen Observablen 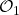 und
und 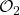 spielt die Reihenfolge der Messung eine Rolle. Messen wir also zuerst
spielt die Reihenfolge der Messung eine Rolle. Messen wir also zuerst 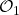 und dann
und dann 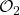 , dann finden wir andere Messwerte als bei der Reihenfolge
, dann finden wir andere Messwerte als bei der Reihenfolge 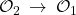 . Der Unterschied dieser Messungen wird mit dem Planckschen Wirkungsquantum
. Der Unterschied dieser Messungen wird mit dem Planckschen Wirkungsquantum 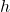 skalieren. Die Messung von
skalieren. Die Messung von 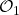 beeinträchtigt also die Messung von
beeinträchtigt also die Messung von 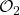 und andersherum.
und andersherum.
Eine direkte Folge dieses Verhaltens ist, dass wir solche Messgrößen 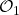 und
und 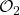 auch nicht gleichzeitig beliebig genau messen können. Wollen wir beide gleichzeitig messen, können wir für beide jeweils nur kleinstmögliche Bereiche angeben, in denen die Messwerte mit einer gewissen Wahrscheinlichkeit liegen werden. Wichtig ist hierbei, dass das nicht an Unzulänglichkeiten der Messapparatur liegt, sondern eine natürliche Grenze ist. Die Messwerte sind also naturgemäß „unscharf“.
auch nicht gleichzeitig beliebig genau messen können. Wollen wir beide gleichzeitig messen, können wir für beide jeweils nur kleinstmögliche Bereiche angeben, in denen die Messwerte mit einer gewissen Wahrscheinlichkeit liegen werden. Wichtig ist hierbei, dass das nicht an Unzulänglichkeiten der Messapparatur liegt, sondern eine natürliche Grenze ist. Die Messwerte sind also naturgemäß „unscharf“.
Messen wir 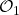 und
und 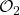 oft genug, werden wir für beide eine statistische Verteilung der Messwerte um die jeweils wahrscheinlichsten Werte, die Erwartungswerte, finden. Die Unschärfen der beiden Messgrößen sind dabei die Varianzen
der beiden Verteilungen. Das Produkt der beiden Varianzen, also der jeweiligen Messungenauigkeiten, ist minimal durch den konstanten Unterschied der Messungen
oft genug, werden wir für beide eine statistische Verteilung der Messwerte um die jeweils wahrscheinlichsten Werte, die Erwartungswerte, finden. Die Unschärfen der beiden Messgrößen sind dabei die Varianzen
der beiden Verteilungen. Das Produkt der beiden Varianzen, also der jeweiligen Messungenauigkeiten, ist minimal durch den konstanten Unterschied der Messungen 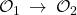 und
und 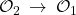 und damit über die Plancksche Konstante gegeben. Das nennt man die „Unschärferelation“ (von
und damit über die Plancksche Konstante gegeben. Das nennt man die „Unschärferelation“ (von 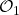 und
und 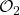 ). Bestimmen wir also
). Bestimmen wir also 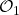 genauer, nimmt automatisch die Unbestimmtheit von
genauer, nimmt automatisch die Unbestimmtheit von 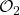 zu und andersherum. Das geht so weit, dass wenn wir zum Beispiel
zu und andersherum. Das geht so weit, dass wenn wir zum Beispiel 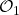 exakt bestimmen wollen,
exakt bestimmen wollen, 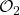 dafür unendlich unscharf wird und in unserer Messung jeden beliebigen Wert annehmen kann.
dafür unendlich unscharf wird und in unserer Messung jeden beliebigen Wert annehmen kann.
Ein solches Paar von Messgrößen sind der Ort 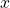 und der Impuls
und der Impuls 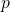 . Ihre Unschärferelation ist die bekannte „Heisenbergsche Unschärferelation“ und lautet für die Varianzen
. Ihre Unschärferelation ist die bekannte „Heisenbergsche Unschärferelation“ und lautet für die Varianzen 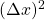 und
und 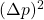 beziehungsweise die Standardabweichungen
beziehungsweise die Standardabweichungen
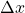 und
und 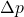
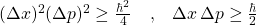 .
.
Wir sehen hier auch, dass solche Unschärferelationen aufgrund der Kleinheit von 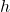 in der klassischen Physik komplett zu vernachlässigen sind.
in der klassischen Physik komplett zu vernachlässigen sind.
Quantisierung des Drehimpulses
In der Quantenmechanik stellt sich heraus, dass Drehimpulse (der klassische Bahndrehimpuls
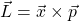 und der quantenmechanische Spin), auch eine Art harmonische Oszillatoren sind. Die Werte von Drehimpulsen, insbesondere des Bahndrehimpulses
und der quantenmechanische Spin), auch eine Art harmonische Oszillatoren sind. Die Werte von Drehimpulsen, insbesondere des Bahndrehimpulses 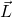 , können also auch nur Vielfache von
, können also auch nur Vielfache von 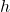 annehmen. Das stimmt auch bezüglich der Einheiten, denn auch
annehmen. Das stimmt auch bezüglich der Einheiten, denn auch 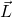 hat die Dimension Energie mal Zeit.
hat die Dimension Energie mal Zeit.
Im Detail finden wir für den Bahndrehimpuls eine Quantisierung sowohl des Gesamtdrehimpulses 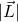 als auch seiner Projektion in eine Richtung, meistens wählt man die
als auch seiner Projektion in eine Richtung, meistens wählt man die  -Richtung,
-Richtung, 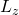 . Mit der „Drehimpulsquantenzahl“
. Mit der „Drehimpulsquantenzahl“ 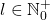 (für den Bahndrehimpuls) ergibt sich
(für den Bahndrehimpuls) ergibt sich
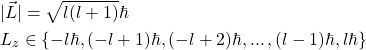 .
.
Die Projektionen des Drehimpulses in verschiedene Richtungen sind solche oben beschriebene unverträgliche Messgrößen. Es ergibt also keinen Sinn, neben 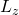 , das einen der
, das einen der 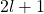 Werte annehmen kann, auch
Werte annehmen kann, auch 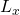 oder
oder 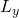 anzugeben. Für den Spin finden wir eine analoge Quantisierung.
anzugeben. Für den Spin finden wir eine analoge Quantisierung.