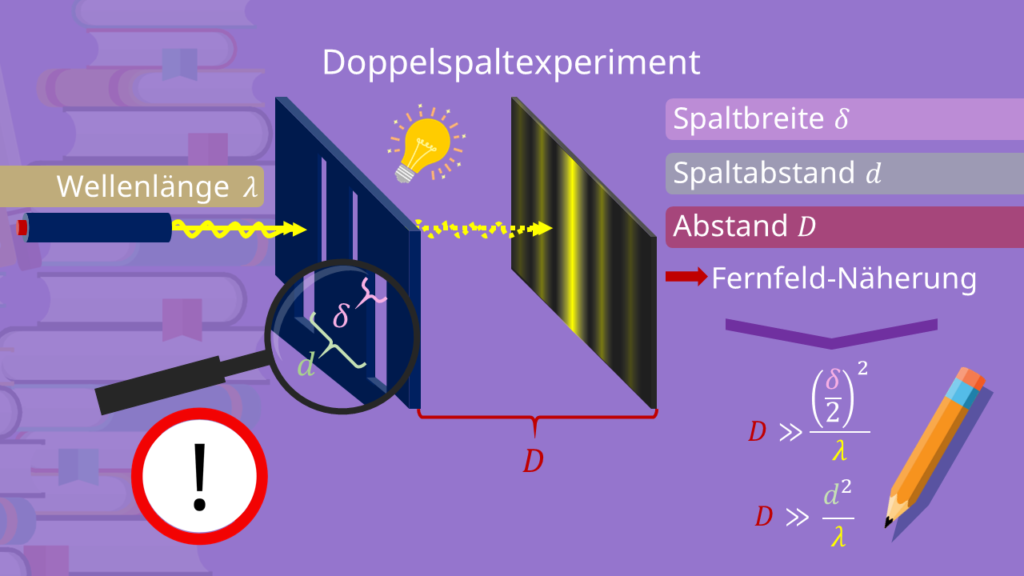
Doppelspaltexperiment Durchführung
Das Doppelspaltexperiment ist eines der Schlüsselexperimente der Physik und kann Dir auf einfache Weise viel über Quantenmechanik verraten. Wenn Du erfahren möchtest, was es so cool macht und was wir aus seinem Interferenzmuster lernen können, dann bist Du hier genau richtig!
Es lohnt sich auch, unser Video zum Doppelspaltversuch anzusehen. Darin haben wir Dir das Thema zum entspannten Lernen nochmals kurz und verständlich aufbereitet.
Inhaltsübersicht
Doppelspaltexperiment einfach erklärt
Das Doppelspaltexperiment ist ein Experiment zur Quantenmechanik, das den Wellencharakter von (masselosen) Photonen und Materieteilchen (Teilchen mit Ruhemasse wie zum Beispiel Elektronen oder Protonen) zeigt. Es liefert daher einen der Hauptbeweise für den Welle-Teilchen-Dualismus .
Beim Doppelspaltversuch wird ein Strahl aus Licht (Photonen) oder Materieteilchen durch zwei schmale, parallele Spalte in einer sonst undurchlässigen Blende gesendet und trifft hinter dieser Blende auf einen Detektor, der die auftreffende Strahlung sichtbar macht. Für passende Verhältnisse aus Spaltbreite, Spaltabstand und Abstand Blende-Detektor lässt sich auf dem Detektor ein Interferenzmuster aus sich abwechselndern Intensitätsmaxima und –minima erkennen. Dieses Muster sieht genau so aus wie bei der Interferenz von Wasserwellen (Superposition einzelner Wellen) in einem Doppelspalt-Setup.
Die Erklärung hierfür ist, dass sowohl Photonen als auch Materieteilchen gleichzeitig einen inhärenten Wellencharakter haben. Dass Teilchen der Quantentheorie sowohl Wellen- als auch Teilcheneigenschaften zeigen, je nach momentaner Wechselwirkung, nennt man den Welle-Teilchen-Dualismus.
Doppelspaltexperiment Aufbau
Wie bereits erwähnt können wir das Doppelspaltexperiment sowohl mit Lichstrahlen als auch mit Strahlen aus Materieteilchen durchführen. Wir wollen den Versuchsaufbau für Licht durchgehen, für Materieteilchen ist er sehr ähnlich.
Hier benötigen wir neben einer Lichtquelle einen optischen Apparat, der das ausgesendete Licht parallelisiert. Zudem funktioniert das Doppelspaltexperiment am besten mit möglichst monochromatischem Licht, also Licht einer möglichst konstanten Wellenlänge 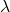 . Laser erfüllen beide Eigenschaften annähernd perfekt und sind daher für Doppelspaltexperimente am besten geeignet. Der (Laser-)Lichtstrahl tritt dann durch den Doppelspalt
und trifft dahinter auf den Detektor. Der Detektor kann in diesem Fall eine einfache weiße Platte sein, auf der wir das Laserlicht gut sehen können. Die zwei Spalte sollen die Breite
. Laser erfüllen beide Eigenschaften annähernd perfekt und sind daher für Doppelspaltexperimente am besten geeignet. Der (Laser-)Lichtstrahl tritt dann durch den Doppelspalt
und trifft dahinter auf den Detektor. Der Detektor kann in diesem Fall eine einfache weiße Platte sein, auf der wir das Laserlicht gut sehen können. Die zwei Spalte sollen die Breite 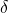 haben und der Spaltabstand soll
haben und der Spaltabstand soll 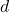 betragen. Der Detektor soll sich im Abstand
betragen. Der Detektor soll sich im Abstand 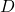 von der Blende befinden.
von der Blende befinden.
Das Doppelspaltexperiment wird in der Fernfeld-Näherung durchgeführt. Das heißt, dass sowohl 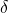 als auch
als auch 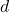 vergleichbar mit
vergleichbar mit 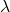 sein müssen, während der
sein müssen, während der 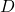 im Vergleich zu
im Vergleich zu 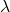 sehr groß sein muss. Im Detail müssen die folgenden Ungleichungen erfüllt sein:
sehr groß sein muss. Im Detail müssen die folgenden Ungleichungen erfüllt sein:
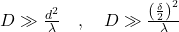 .
.
Doppelspaltexperiment Beobachtung
Gemäß dem Photoeffekt
stellen wir uns Photonen genauso wie Materieteilchen als wirkliche Teilchen, also kleine „Kügelchen“ vor. Daher erwarten wir gemäß unserer Intuition aus der klassischen Physik für die Intensitätsverteilung auf dem Detektor zwei klare Peaks der Spaltbreite 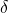 direkt hinter den beiden Spalten. Diese Intuition stellt sich als falsch heraus!
direkt hinter den beiden Spalten. Diese Intuition stellt sich als falsch heraus!
Experiment mit (Laser-)Licht
Wird das Doppelspaltexperiment mit (Laser-)Licht durchgeführt, können wir auf dem Detektor ein symmetrisches Muster aus sich abwechselnden hellen und dunklen Streifen (Intensitätsmaxima und –minima) beobachten, die kontinuierlich ineinander übergehen. Die dunklen Streifen sind dabei viel schmaler als die Hellen. Dieses Intensitätsmuster ist symmetrisch bezüglich des hellsten Intensitätsmaximums, das sich genau zwischen den beiden Spalten befindet. Nach außen hin nehmen die Maxima an Helligkeit ab. Verändern wir die Wellenlänge unseres Lasers (im Rahmen der Fernfeldnäherung), so sehen wir eine Verschiebung der Maxima (außer des Zentralen), jedoch bleibt die Gestalt des Musters dieselbe. Auch Änderungen des Spaltabstands und des Abstands Blende-Detektor verschieben die Maxima und Minima.
Wir beobachten also nicht zwei gleiche, diskrete Intensitätsmaxima hinter den Spalten, sondern eine viel kompliziertere Intensitätsverteilung.
Experiment mit einzelnen Photonen
Wir können das Doppelspaltexperiment auch mit einer Photonenquelle durchführen, die nur in genügend großen zeitlichen Abständen und nur einzelne Photonen konstanter Energie emittiert (es treten also stets nur einzelne Photonen derselben Wellenlänge durch den Doppelspalt). In diesem Fall können wir natürlich nicht direkt ein Muster erkennen. Stellt unser Detektor ein auftreffendes Photon zum Beispiel als einzelnen, hellen Punkt dar, dann sehen wir zu Beginn nur einzelne, scheinbar willkürlich verteilte leuchtende Punkte. Mit der Zeit treffen jedoch mehr und mehr Photonen auf dem Detektor auf und es baut sich eine Intensitätsverteilung derselben Gestalt auf.
Experimente mit Materieteilchen
Nun verwenden wir für das Doppelspaltexperiment einen Strahl aus Materieteilchen ähnlich Licht (kontinuierlicher Strahl, viele „gleichzeitige“ Teilchen) und einzelne Materieteilchen. In beiden Fällen erhalten wir Intensitätsverteilungen, deren Gestalt genau denen aus unseren Versuchen mit (Laser-)Licht beziehungsweise mit einzelnen Photonen entspricht.
Versuch einer Wegbestimmung
Zuletzt können wir versuchen, eine Apparatur einzubauen, mit der wir bestimmen können durch welchen der beiden Spalte die Teilchen den Detektor erreichen. Beispielsweise können wir ganz simpel einen Spalt verschließen. Eine andere Möglichkeit beim Experiment mit Photonen ist das Einbringen von zueinander senkrechten Polarisationsfiltern in die beiden Spalte. Erzeugen wir beliebige Photonen mit Polarisationen nur in diesen beiden Richtungen, können diese jeweils nur einen der beiden Spalte „benutzen“.
Egal welche Methode wir wählen, sowie wir versuchen, eine Information darüber zu erhalten, durch welchen der beiden Spalte sich die Teilchen jeweils bewegen, wird das Intensitätsmuster zerstört. Dann sehen wir nur noch das Beugungsbild eines oder zweier Einfachspalte. Ob wir dabei die „Welcher-Weg-Information“ tatsächlich erhalten (verschlossener Spalt) oder nur die Möglichkeit dazu hätten (Polarisationsfilter) spielt keine Rolle. Zudem ist es irrelevant, ob wir unsere Apparatur vor oder direkt hinter dem Doppelspalt (Quantenradierer) installieren.
Interferenzmuster berechnen
Die Berechnung und die Interpretation zeigen wir in unserem nächsten Video – schau vorbei!
Die beobachteten Intensitätsverteilungen entsprechen in ihrer Gestalt denen bei der Interferenz von Wasserwellen an einem Doppelspalt. Setzen wir also auch hier das Huygenssche Prinzip an und sehen jeden Spalt als Ausgangspunkt von elementaren Kugelwellen an. Der Weg von einem Spalt zum Punkt  ist im Allgemeinen ungleich dem Weg vom anderen Spalt aus. Daraus resultiert ein Gangunterschied
ist im Allgemeinen ungleich dem Weg vom anderen Spalt aus. Daraus resultiert ein Gangunterschied 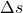 zwischen den Wellen von
zwischen den Wellen von
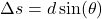
mit dem Spaltabstand 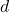 . Zudem entnehmen wir der Versuchsskizze
. Zudem entnehmen wir der Versuchsskizze
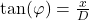 .
.
Da wir die Gültigkeit der Fernfeldnäherung voraussetzen, ist der Abstand 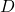 zum Detektor in Wirklichkeit viel größer als er in der Versuchsskizze erscheint. Tatsächlich sind die Wege der ausgehenden Wellen nahezu parallel. Daher finden wir
zum Detektor in Wirklichkeit viel größer als er in der Versuchsskizze erscheint. Tatsächlich sind die Wege der ausgehenden Wellen nahezu parallel. Daher finden wir 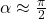 und erhalten damit
und erhalten damit
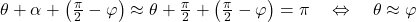 .
.
Zudem können wir die Kleinwinkelnäherung für 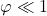 verwenden:
verwenden:
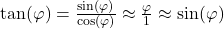 .
.
Wir kombinieren beide Resultate mit der Formel für den Gangunterschied und erhalten
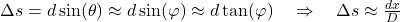
mit Spaltabstand 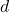 und Abstand Blende-Detektor
und Abstand Blende-Detektor 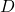 .
.
Interferenzmaxima
Interferenzmaxima treten bei konstruktiver Interferenz auf, also wenn sich die Wellen „identisch überlagern“. Der Gangunterschied 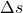 muss dann ein ganzzahliges Vielfaches der Wellenlänge
muss dann ein ganzzahliges Vielfaches der Wellenlänge 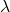 sein
sein
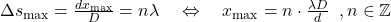 .
.
Dabei entspricht 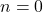 dem zentralen Maximum.
dem zentralen Maximum.
Interferenzminima
Intensitätsminima finden wir wenn sich die Wellen „genau entgegengesetzt überlagern“, sogenannte destruktive Interferenz. Dazu muss der Gangunterschied ein ungerades Vielfaches der Wellenlänge  sein
sein
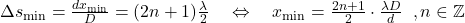 .
.
Formel Intensitätsverteilung
Eine korrekte Berechnung der Intensität 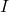 in Abhängigkeit des Winkels
in Abhängigkeit des Winkels 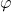 ergibt die folgende Verteilung
ergibt die folgende Verteilung
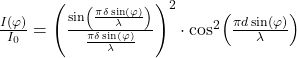
mit der Intensität des zentralen Maximums 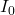 und der Spaltbreite
und der Spaltbreite 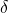 . Diese Funktion ist ein Produkt aus der Intensität bei Beugung am Einfachspalt, gegeben durch den ersten Faktor (schwarze einhüllende Kurve im Plot), und der Intensität zweier Punktquellen im Abstand
. Diese Funktion ist ein Produkt aus der Intensität bei Beugung am Einfachspalt, gegeben durch den ersten Faktor (schwarze einhüllende Kurve im Plot), und der Intensität zweier Punktquellen im Abstand 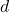 , gegeben durch den
, gegeben durch den 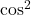 -Term (rote Kurve im Plot). Die Einhüllende bestimmt dabei Stärke sowie Lage der Maxima und der Punktquellenterm beschreibt die genaue Lage der Maxima und Minima.
-Term (rote Kurve im Plot). Die Einhüllende bestimmt dabei Stärke sowie Lage der Maxima und der Punktquellenterm beschreibt die genaue Lage der Maxima und Minima.
Da gilt 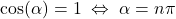 und
und 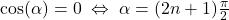 mit
mit 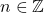 finden wir unsere Bedingungen für die Maxima und Minima bestätigt
finden wir unsere Bedingungen für die Maxima und Minima bestätigt
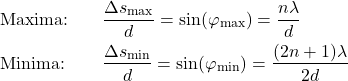
Zudem können wir aus dieser Funktion ablesen, wie sich Veränderungen in der Doppelspaltgeometrie oder der Wellenlänge auf das Interferenzmuster auswirken:
- Verbreiterung/Verschmälerung der Spaltbreite

Verschmälerung/Verbreiterung der Einhüllenden - Vergrößerung/Verkleinerung des Spaltabstands

Maxima und Minima liegen enger beieinander/weiter auseinander - Vergrößerung/Verkleinerung der Wellenlänge

Einhüllende wird breiter/schmäler und Interferenzmaxima liegen weiter auseinander/enger beieinander
Doppelspaltexperiment Interpretation
Wie lassen sich die Beobachtungen beim Doppelspaltexperiment nun interpretieren? Durch den Vergleich mit der Interferenz von Wasserwellen und den Ansatz von Teilchen als Wellen gemäß dem Welle-Teilchen-Dualismus der Quantentheorie konnten wir das Interferenzmuster korrekt berechnen. Doch wie können wir uns das vorstellen?
Die Teilchen, Photonen oder Materieteilchen, mit denen wir das Doppelspaltexperiment durchgeführt haben, sind Quantenteilchen. In der nichtrelativistischen Quantenmechanik werden Teilchen über sogenannte Wellenfunktionen beschrieben. Eine der entscheidenden Eigenschaften dieser Wellenfunktionen im Gegensatz zur klassischen Physik ist ihre rein statistische Natur. Wellenfunktionen sind gegeben als Superpositionen aller möglichen Zustände kombiniert mit den entsprechenden Wahrscheinlichkeiten. Im Beispiel des Doppelspalts besteht die Wellenfunktion also zu 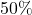 aus dem Anteil für ein Teilchen im einen und zu
aus dem Anteil für ein Teilchen im einen und zu 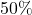 aus dem Anteil für ein Teilchen im anderen Spalt.
aus dem Anteil für ein Teilchen im anderen Spalt.
Der zweite wichtige Unterschied der Quantenmechanik zur klassischen Physik ist die Art des Messprozesses. Während wir in der klassischen Physik immer, überall und prinzipiell ohne Beeinträchtigung des physikalischen Systems messen können, ist das in der Quantenmechanik nicht möglich. Hier muss die Messung als die Interaktion zweier quantenmechanischer Systeme angesehen werden, die sie ist. Und eine solche Interaktion beeinflusst beide Seiten: sowohl den Messapparat als auch das vermessene System. Ohne eine solche Messung aber gibt es keine Information über das System und es könnte für den Messenden genauso gut nicht existieren.
Kopenhagener Deutung
Die gängigste Interpretation des Messprozesses der Quantenmechanik ist die Kopenhagener Deutung. Sie besagt, dass die Messung einer Wellenfunktion nicht nur einen der durch die Superposition möglichen Messwerte ergibt, sondern gleichzeitig die Wellenfunktion auf den entsprechenden Zustand in ihrer Superposition festlegt. Der Messprozess stellt den gemessenen Zustand also nicht fest, sondern her. Das nennt man den Kollaps der Wellenfunktion. Dieser Messwert wird aber nur mit seiner entsprechenden Wahrscheinlichkeit gemessen und bei der nächsten Messung könnte einer der anderen Messwerte mit entsprechendem Teil der Wellenfunktion realisiert werden. Der Messprozess ist also nicht oder nur statistisch deterministisch in seiner Aussage, ganz im Gegensatz zur klassischen Physik. Und das liegt nicht an Unzulänglichkeiten des Messapparats, sondern ist eine fundamentale Eigenschaft der Natur.
Das erklärt auch, warum die “Welcher-Weg-Information“ das Interferenzmuster zerstört. Die Wellenfunktion eines Teilchens nach dem Doppelspalt ist eine Superposition zweier Anteile, die jeweils alle möglichen Wege nach einem der beiden Spalte beschreiben. Erst am Detektor wird der Ort des Teilchens gemessen und die beiden Teile der Wellenfunktion interferieren zum bekannten Interferenzmuster. Das Teilchen “benutzt also beide Spalte gleichzeitig“ und “interferiert mit sich selbst“. Messen wir jedoch schon vorher den vom Teilchen benutzen Weg, zum Beispiel mit den Polarisationsfiltern, finden wir es in einem der beiden Spalte, aber legen es mit dem Ergebnis gleichzeitig auf den entsprechenden Spalt fest. Dadurch kollabiert die Wellenfunktion auf den zum jeweiligen Spalt gehörigen Anteil und die Interferenz wird unmöglich. In Summe vieler Teilchen sehen wir die Beugungsbilder der beiden Einfachspalte.
Viele-Welten-Theorie
Eine der anderen Interpretation des quantenmechanischen Messprozesses ist die Viele-Welten-Theorie. Sie geht davon aus, dass bei jeder Messung alle Möglichkeiten der Wellenfunktion realisiert werden, jedoch in einer Art “Verzweigung“ des Universums. Es ensteht eine Kopie des Universums für jeden Messwert, jedoch ohne die Möglichkeit, dass diese verschiedenen Universen miteinander interagieren könnten. Daher ist die Messung, obwohl insgesamt deterministisch, für jeden einzelnen Beobachter, der wieder nur einen Messwert misst, ebenso statistisch wie in der Kopenhagener Deutung.