Nernst Gleichung
In der Elektrochemie ist dir die Nernst Gleichung schon einmal begegnet? Sehr gut! Hier und in unserem Video erklären wir dir, was genau sie besagt und wie du sie herleiten kannst! Außerdem zeigen wir die Anwendung der Nernst Gleichung in einem sehr ausführlichen Beispielkapitel.
Inhaltsübersicht
Nernst Gleichung einfach erklärt
Zuerst einmal sollte man klären, was die Nernst Gleichung (engl. :Nernst equation) überhaupt ist. Diese kommt aus dem Gebiet der Elektrochemie.
Merke: Dort benutzt man die Nernst Gleichung, um zu bestimmen, welche Spannung zwischen zwei Halbzellen eines galvanischen Elements herrscht.
Diese Spannung variiert mit den Konzentrationen der Reaktanden in den einzelnen Halbzellen, was die Nernst Gleichung auch versucht, zu beschreiben.
Nernst Gleichung Herleitung
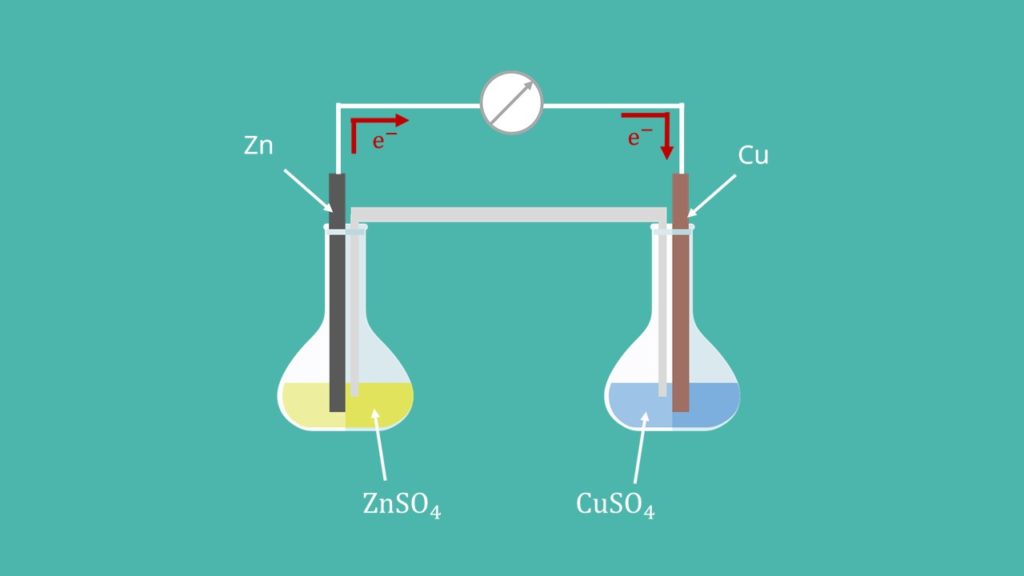
Am besten versteht man die Nernst-Gleichung, wenn man sich klar macht, wie man sie herleitet. Wie bereits gesagt, wurde die Nernstsche Gleichung hauptsächlich für den Gebrauch an galvanischen Zellen eingeführt. Bei diesen wusste man , dass eine Redoxreaktion stattfindet zwischen den beiden Halbzellen. Dabei gibt die Seite, auf der die Oxidation stattfindet Elektronen ab. Diese werden über einen elektrischen Leiter auf die andere Halbzelle übertragen, auf der damit die Reduktion stattfindet.
Beschreibung der Spannung über den fließenden Strom
Dieser Strom kommt ursächlich durch eine Spannung zwischen der Oxidations– und der Reduktions Halbzelle zustande. Die Energie, die man über den Strom dabei abgreifen kann, lässt sich so beschreiben:
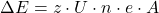
ΔE= gewonnene Energie ; z= Anzahl an Ladungen, die bei Redoxreaktion frei wird; U=Spannung zwischen den Halbzellen; e=Elementarladung n=Stoffmenge; A=Avogadrokonstante
Dabei wird noch für das Produkt 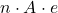 die Faradaykonstante F eingeführt, die aussagt, wie viel Ladung in einem Mol gespeichert ist. Für den Fall, dass jedes Atom des Mols ein Elektron abgibt. Dann ergibt sich:
die Faradaykonstante F eingeführt, die aussagt, wie viel Ladung in einem Mol gespeichert ist. Für den Fall, dass jedes Atom des Mols ein Elektron abgibt. Dann ergibt sich:
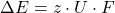
Einführung der Konzentrationsabhängigkeit der Spannung
Diese Beschreibung der Spannung reichte jedoch nicht. Denn man beobachtete, dass die Spannung mit fortschreitender Redoxreaktion kleiner wurde, nämlich in dem Maße, in dem auch die Konzentration der Edukte kleiner geworden ist. Deshalb suchte man nach einem Ausdruck für die Energie, der die Abhängigkeit zwischen der frei werdenden Energie und den Konzentrationen angibt. Dafür nahm man die freie Reaktionsenthalpie 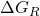 her. Sie ist folgendermaßen definiert:
her. Sie ist folgendermaßen definiert:
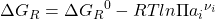
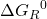 = Standardreaktionsenthalpie;
= Standardreaktionsenthalpie;
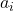 = Aktivität von Stoff (i);
= Aktivität von Stoff (i);
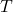 = Temperatur;
= Temperatur;
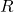 = ideale Gaskonstante
= ideale Gaskonstante
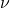 = stöchiometrischer Koeffizient (positives Vorzeichen für Produkte, negatives Vorzeichen für Edukte!)
= stöchiometrischer Koeffizient (positives Vorzeichen für Produkte, negatives Vorzeichen für Edukte!)
Diese gibt an, welche Änderung der freien Enthalpie eintritt, wenn z.B. in folgender Reaktionsgleichung Edukte zu Produkten reagieren:
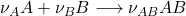
Die freie Enthalpie hat man hier deswegen gewählt, da sie bei konstantem Druck und konstanter Temperatur die Menge an Arbeit angibt, die das System bei der Reaktion über die Druck-Volumen Arbeit hinaus verrichtet. Dieser Teil der Arbeit entspricht genau der Energie, die man als Spannung von der galvanischen Zelle abgreifen kann. Auch konstanter Druck und konstante Temperatur lassen sich bei einer galvanische Zelle gut als Näherung annehmen.
Da beide Gleichungen dieselbe Energie beschreiben, kann man sie gleichsetzen und daraus die Nernst Gleichung herleiten:
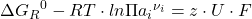
Allgemeine Form der Nernst Gleichung
Um die allgemeine Form der Nernst Gleichung zu erhalten, muss man nur noch einen leichten Schritt gehen. Man stellt die Gleichung nur noch nach der Spannung U um und erhält die allgemeine Nernst Gleichung:
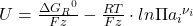
Der Term 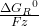 ist konstant und wird meist gleich
ist konstant und wird meist gleich 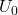 gesetzt, sie drückt die Spannung in den Standardzuständen aus, also das Standardpotential. Diese kann für jede beliebige Kombination von Reaktionspartnern in den verschiedenen Halbzellen in der elektrochemischen Spannungsreihe
nachgeschlagen werden.
gesetzt, sie drückt die Spannung in den Standardzuständen aus, also das Standardpotential. Diese kann für jede beliebige Kombination von Reaktionspartnern in den verschiedenen Halbzellen in der elektrochemischen Spannungsreihe
nachgeschlagen werden.
Nun zur eigentlich gewollten Konzentrationsabhängigkeit der Spannung in der Nernst Gleichung: Diese geht in der Formel als Aktivität 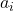 ein, denn wenn man geringe Konzentrationen in den Halbzellen voraussetzt, lassen sich diese durch die entsprechenden Konzentrationen annähern. Dadurch vereinfacht sich die Nernst Gleichung zu:
ein, denn wenn man geringe Konzentrationen in den Halbzellen voraussetzt, lassen sich diese durch die entsprechenden Konzentrationen annähern. Dadurch vereinfacht sich die Nernst Gleichung zu:
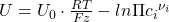
Wenn man sich diese Nernst Gleichung genauer ansieht, erkennt man, dass mit steigenden Konzentrationen der ln-Term immer größer wird und damit die elektrische Spannung sinkt. Somit gibt die Gleichung das beobachtete Verhalten also auch wieder.
Angewandte Form der Nernst Gleichung
Trotz der Allgemeingültigkeit der obigen Form der Nernst Gleichung sieht man sie doch oft in der folgenden, praktischeren Form:
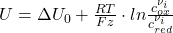
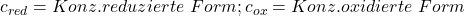
Das liegt daran, dass diese Form die Berechnung etwas vereinfacht. In dieser Form muss man nicht auf das Vorzeichen der stöchiometrischen Koeffizienten achten und kann daher für die beiden Halbzellen eines galvanischen Elements dieselbe Formel verwenden. Des Weiteren kann man in dieser Form auch die Standardpotentiale aus der elektrochemischen Spannungsreihe verwenden, die generell nur Reduktionsreaktionen mit der 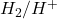 -Halbzelle zeigt. Das vereinfacht die Rechnungen stark.
-Halbzelle zeigt. Das vereinfacht die Rechnungen stark.
Bestimmung der Anzahl an übertragenen Elektronen z
Um den ersten wichtigen Paramerter z in der Nernst Gleichung zu bestimmen, stellt man zuerst die Redoxgleichungen für die Halbzellen auf. Auf der linken Seite hat man die Oxidationsseite. Hier wird elementares Zink zu Zink-Ionen oxidiert, die dann in Lösung gehen:
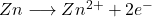
Auf der rechten Seite findet die Reduktion von Kupfer-Ionen aus der Lösung zu elementarem Kupfer statt mit den Elektronen des oxidierten Zinks:
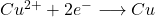
Anhand der Redoxgleichungen kann man also feststellen, wie viele Elektronen z in der Nernst Gleichung übertragen werden. Hier also in beiden Halbzellen z=2.
Restliche Annahmen für die Nernst Gleichung
Nimmt man weiter an, dass sich auf den jeweiligen Seiten der galvanischen Zelle anfangs eine 1 molare Zinksulfat-Lösung (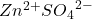 ) bzw. eine 1 molare Kupfersulfat-Lösung (
) bzw. eine 1 molare Kupfersulfat-Lösung (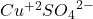 ) befindet, hat man alle nötigen Informationen, um die abgreifbare Spannung zu berechnen:
) befindet, hat man alle nötigen Informationen, um die abgreifbare Spannung zu berechnen:
T=25°C, z=2 (siehe Redoxgleichungen) c(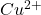 )=1mol/l ; c(
)=1mol/l ; c(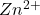 )=1mol/l ;
)=1mol/l ; 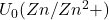 =-0,76V ;
=-0,76V ;
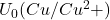 =+0,35V
=+0,35V
Die beiden Werte für die Standardpotentiale 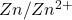 bzw.
bzw. 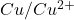 kannst du in der elektrochemischen Spannungsreihe nachschlagen.
kannst du in der elektrochemischen Spannungsreihe nachschlagen.
Einsetzen der Parameter in die Nernst Gleichung
Nun sind alle nötigen Parameter bestimmt und du kannst sie in der Nernst Gleichung anwenden. Da die elektrochemische Spannungsreihe jeweils Spannungswerte für jedes Redoxpaar relativ zur Wasserstoff-Halbzelle liefert, kann man die Nernst Potentiale der Halbzellen jeweils einzeln berechnen und dann voneinander abziehen:
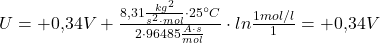
Dabei wurde vereinfachend angenommen, dass die Konzentration vom elementarem Kupfer gleich 1 ist. Das kann man allgemein für alle an der Reaktion beteiligten Feststoffe und auch für Wasser machen, sollte dieses mitreagieren. Das ist deswegen zulässig, da diese Stoffe nahezu in ihren reinen Standardzuständen vorliegen. Man muss auf jeden Fall immer sicher gehen, dass die stöchiometrischen Koeffizienten aus den Redoxgleichungen als Exponenten der Konzentrationen mit berücksichtigt sind. Hier sind sie beide gleich 1, darum gehen die Konzentrationen nur mit dem Exponenten 1 in die Gleichung ein.
Im nächsten Schritt berechnet man das Potential für die Zink Halbzelle, dort kann man analog vorgehen und die Nernst Gleichung so aufstellen:
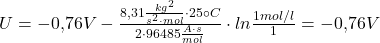
In einem letzten Schritt muss man nur noch das Potential der Oxidations-Halbzelle von der Reduktions-Halbzelle abziehen und man erhält die Gesamtspannung zwischen den Halbzellen:
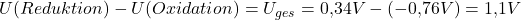
Beachte aber dabei, dass diese Spannung nur ganz am Anfang abgreifbar ist. Sie wird sich dadurch, dass sich die Konzentrationen der Ionen in den Halbzellen ändern, mit der Zeit reduzieren!
Nernstgleichung bei Konzentrations-Zellen
Man kann eine Spannung aber auch über zwei gleiche Halbzellen, also z.B. zwei Kupferhalbzellen, erzeugen. Dafür muss man nur die Konzentrationen der Kupfersulfat-Lösungen zwischen den beiden variieren. Denn das Nernst Potential einer Halbzelle ist ja konzentrationsabhängig, wie die Nernst Gleichung es auch beschreibt.
Nimmt man z.B. eine Kupferhalbzelle mit einer 1 molaren 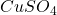 -Lösung und eine andere Kupferhalbzelle mit einer 0,1 molaren
-Lösung und eine andere Kupferhalbzelle mit einer 0,1 molaren 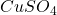 -Lösung und verbindet diese, dann entsteht eine Spannung. Dabei wird immer in der Zelle mit der geringeren
-Lösung und verbindet diese, dann entsteht eine Spannung. Dabei wird immer in der Zelle mit der geringeren 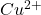 –Konzentration oxidiert und Cu-Ionen gehen in Lösung, während in der Zelle mit der höheren, anfänglichen
–Konzentration oxidiert und Cu-Ionen gehen in Lösung, während in der Zelle mit der höheren, anfänglichen 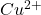 -Ionen Konzentrationen reduziert wird und elementares Kupfer entsteht. Somit gleicht sich der Konzentrationsunterschied mit fortlaufender Reaktion immer weiter an. Man kann für die Halbzelle mit der höheren Ionen-Konzentration (1mol/l) dann folgende Gleichungen aufstellen:
-Ionen Konzentrationen reduziert wird und elementares Kupfer entsteht. Somit gleicht sich der Konzentrationsunterschied mit fortlaufender Reaktion immer weiter an. Man kann für die Halbzelle mit der höheren Ionen-Konzentration (1mol/l) dann folgende Gleichungen aufstellen:
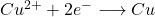
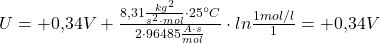
Und für die Halbzelle mit der geringeren Ionen-Konzentration (0,1 mol/l):
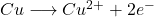
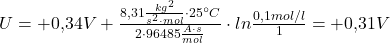
Und wenn man wieder das Nernst Potential der Reduktions-Halbzelle minus das der Oxidations-Halbzelle rechnet, ergibt sich die Gesamtspannung:
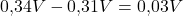
Nernstsche Gleichung pH Abhängigkeit
Man kann mithilfe der Nernst Gleichung sogar den pH-Wert messen. Um das Grundprinzip zu verstehen, stellt man sich am besten wieder zwei Konzentrations-Halbzellen vor. Nur dieses Mal nicht mit dem Redoxpaar 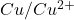 , sondern mit folgendem Redoxpaar:
, sondern mit folgendem Redoxpaar: 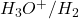 . Es werden also Oxoniumionen in Wasserstoffgas umgewandelt und umgekehrt beim Ablauf der Reaktion in den Halbzellen:
. Es werden also Oxoniumionen in Wasserstoffgas umgewandelt und umgekehrt beim Ablauf der Reaktion in den Halbzellen:
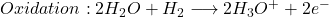
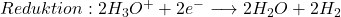
Besteht eine Konzentrationsdifferenz der Oxonium-Ionen 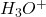 , besteht auch eine Differenz in den pH-Werten, da der pH-Wert nichts anderes ist als der negative dekadische Logarithmus der Oxonium-Ionen Konzentration. Diese Konzentrationsdifferenz der Oxonium-Ionen bewirkt dann wieder gemäß der Nernst Gleichung eine Spannung, die man messen kann.
, besteht auch eine Differenz in den pH-Werten, da der pH-Wert nichts anderes ist als der negative dekadische Logarithmus der Oxonium-Ionen Konzentration. Diese Konzentrationsdifferenz der Oxonium-Ionen bewirkt dann wieder gemäß der Nernst Gleichung eine Spannung, die man messen kann.
Beispiel für die pH Wert Berechnung
Nehmen, wir beispielhaft an, wir hätten eine Halbzelle mit der Oxonium-Ionen Konzentration 0,1mol/l (pH=1) und eine Halbzelle mit der Oxonium-Ionen Konzentration 1mol/l (pH=0), dann könnte man die Nernst Potentiale der Halbzellen auch anhand des pH-Werts berechnen. Dafür stellt man die Nernst Gleichung erst wie gehabt auf. In der Halbzelle mit größerem pH-Wert wird aufgrund der geringeren Oxonium-Ionen Konzentration oxidiert:
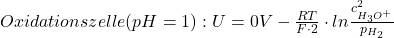
p=Partialdruck (Da 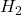 hier gasförmig ist, wird seine Aktivität über den Partialdruck genähert)
hier gasförmig ist, wird seine Aktivität über den Partialdruck genähert)
Man sollte beim Aufstellen der Nernst Gleichung darauf achten, dass die Konzentration der Oxonium-Ionen quadratisch eingeht, aufgrund seines stöchiometrischen Koeffizienten.
Im nächsten Schritt muss man den natürlichen Logarithmus gegen den dekadischen Logarithmus austauschen durch den Umrechnungsfaktor ln10. Des Weiteren kann man den Partialdruck von Wasserstoff auch wieder annäherungsweise gleich 1 setzen. Dadurch ergibt sich folgende Formel:
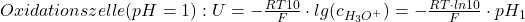
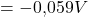
Für die Reduktionszelle geht man wieder analog vor und stellt die Nernst Gleichung folgendermaßen auf:
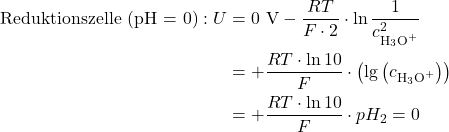
Wenn man dann die beiden Halbzellen Potentiale voneinander abzieht, ergibt sich:
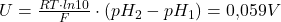
pH Wert Messen in der Praxis
Wenn man in der Praxis also den pH-Wert berechnen will, baut man eine Halbzelle mit bekanntem pH-Wert und verbindet sie leitend mit der Lösung mit unbekanntem pH-Wert. Damit sich die Spannung nicht ändert, erhöht man den elektrischen Widerstand so stark, dass kein Strom und damit auch keine Reaktion stattfindet. Dadurch bleiben die Konzentrationen konstant und die Spannung ändert sich auch nicht. Über das Messen der Spannung mit einem Voltameter kann man dann über die Nernst Gleichung auf den unbekannten pH-Wert schließen.