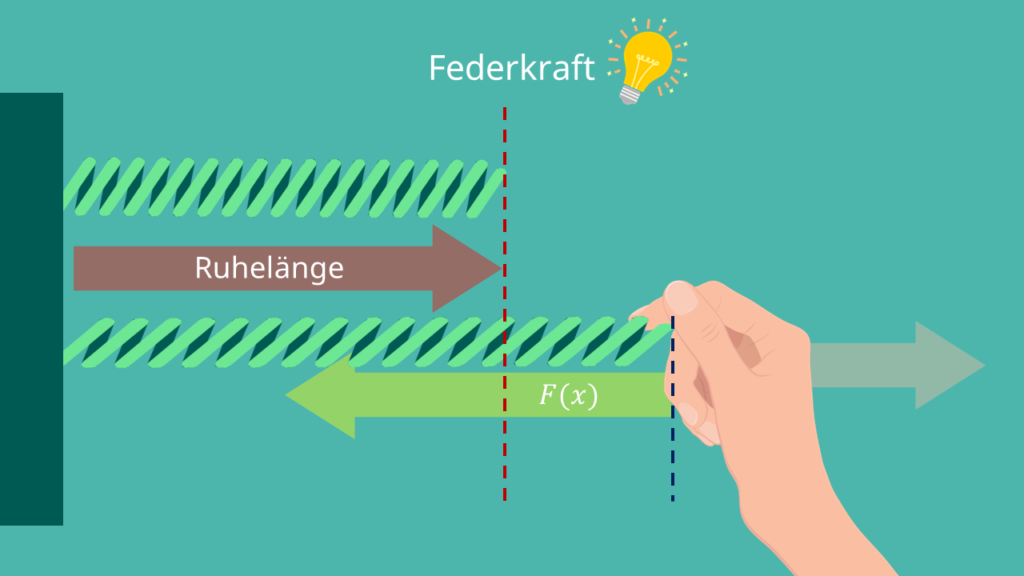
Federkraft
Du hast bestimmt mal davon gehört, dass Federn potentielle Energie speichern können. Federn ermöglichen diesen Prozess, weil sie auf eine Änderung ihrer Länge mit einer Kraft reagieren, die sogenannte Federkraft. In diesem Beitrag wollen wir dir die Federkraft näher bringen.
Bevor wir loslegen, möchten wir dich auf unser Video zum Thema Federkraft aufmerksam machen. Durch das Verbinden des Lesens mit einer audiovisuellen Unterstützung, fällt es dir leichter das Gelernte im Gedächtnis zu behalten.
Inhaltsübersicht
Federkraft einfach erklärt
Wird ein Körper elastisch verformt , so möchte er in seine Ursprungsform zurückkehren. Der Körper versucht das zu erreichen, indem er mit einer Kraft antwortet, der sogenannten Federkraft (Spannkraft, seltener auch Federspannkraft). Die Federkraft ist das Negative des Produkts aus Federkonstante und Änderung der Ruhelänge, F = -k•x.
Vielleicht hast du mal an einer Spiralfeder gezogen und gemerkt, dass es schwieriger wird, je weiter du die Feder ziehst. Das hat damit zu tun, dass die Feder ihre Ruhelänge beibehalten möchte. Dies versucht die Feder zu erreichen, indem sie auf deine Hand die Federkraft ausübt. Nimmst du eine andere Feder, so wird sich dein Kraftaufwand ändern, um die Ruhelänge um den gleichen Betrag zu ändern. Das lässt sich kompakt in eine Formel schreiben, die auch als das Hookesche Gesetz bezeichnet wird.
Die Federkraft (Spannkraft) kannst du mit folgender Formel (Hookesches Gesetz) ausrechnen
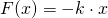 .
.
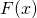 beschreibt die Federkraft (Spannkraft) in
beschreibt die Federkraft (Spannkraft) in 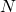 in Abhängigkeit einer Änderung der Ruhlänge. Die Federkonstante in der Einheit
in Abhängigkeit einer Änderung der Ruhlänge. Die Federkonstante in der Einheit 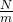 ist mit
ist mit 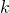 bezeichnet, die Änderung der Ruhelage mit der Einheit
bezeichnet, die Änderung der Ruhelage mit der Einheit 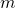 wir mit
wir mit 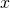 angegeben.
angegeben.
Federkraft berechnen
Wollen wir uns doch ein kleines Beispiel zur Berechnung der Federkraft anschauen. Angenommen wir haben eine Feder mit einer Federkonstante von 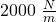 und wir ändern ihre Ruhelänge um
und wir ändern ihre Ruhelänge um 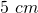 . Mit welcher Kraft wird die Feder dann an unserer Hand ziehen? Lass uns erstmal untersuchen, ob wir Einheiten umrechnen müssen. Wir haben die Federkonstante in
. Mit welcher Kraft wird die Feder dann an unserer Hand ziehen? Lass uns erstmal untersuchen, ob wir Einheiten umrechnen müssen. Wir haben die Federkonstante in 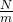 und die Änderung der Ruhelage in
und die Änderung der Ruhelage in 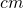 . Das Ergebnis am Ende der Berechnung ist eine Kraft, die die Einheit
. Das Ergebnis am Ende der Berechnung ist eine Kraft, die die Einheit 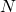 besitzt. Wir müssen also entweder
besitzt. Wir müssen also entweder 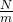 in
in 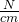 umwandeln oder
umwandeln oder 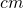 in
in 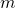 . Das Letzte ist deutlich einfacher und das werden wir auch machen. Die Federkraft berechnet sich also zu
. Das Letzte ist deutlich einfacher und das werden wir auch machen. Die Federkraft berechnet sich also zu
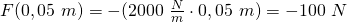 .
.
Nachdem wir also die Feder um 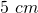 nach rechts gezogen hat, wird sie mit einer Kraft von
nach rechts gezogen hat, wird sie mit einer Kraft von 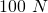 unsere Hand nach links ziehen. Das Minuszeichen steckt dabei im „nach links ziehen“. Merke dir, wie bei allen Rechnungen in der Physik, dass auch beim Berechnen der Spannkraft die Einheiten auf beiden Seiten der Gleichung übereinstimmen. Die Spannkraft wird in Newton gemessen, also muss sowohl links als auch rechts als Einheit Newton rauskommen.
unsere Hand nach links ziehen. Das Minuszeichen steckt dabei im „nach links ziehen“. Merke dir, wie bei allen Rechnungen in der Physik, dass auch beim Berechnen der Spannkraft die Einheiten auf beiden Seiten der Gleichung übereinstimmen. Die Spannkraft wird in Newton gemessen, also muss sowohl links als auch rechts als Einheit Newton rauskommen.
Federkraft Formel
In diesem Abschnitt schauen wir uns die Formel für die Spannkraft
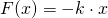
genauer an. Wir zeigen dir eine Herleitung aus experimentellen Beobachtungen und erläutern kurz das Hookesche Gesetz.
An dieser Stelle solltest du dich nicht davon irritieren lassen, dass wir für Änderung der Ruhelänge 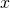 verwenden. Das ist nur ein Platzhalter für eine durch die Problemstellung konkret festgelegte Zahl. Du könntest stattdessen auch jeden anderen Buchstaben verwenden. In der Tat findest du oft auch den Buchstaben
verwenden. Das ist nur ein Platzhalter für eine durch die Problemstellung konkret festgelegte Zahl. Du könntest stattdessen auch jeden anderen Buchstaben verwenden. In der Tat findest du oft auch den Buchstaben  in der Formel für die Spannkraft.
in der Formel für die Spannkraft.
Herleitung aus experimentellen Beobachtungen
Nehmen wir an, dass du eine Spiralfeder vor dir liegen hast. Du nimmst eines der beiden Federenden und fixierst es. Nun ziehst du etwas an dem anderen Ende der Feder. Du wirst dabei etwas bemerken: Je weiter du das Federende ziehst, umso mehr Kraft musst du aufwenden, um es noch ein kleines Stückchen weiterziehen zu können. Die Feder übt auf deine Hand die Federkraft aus, die dem Ziehen entgegenwirkt.
Wir können also schon einmal festhalten, dass die Federkraft (Spannkraft) etwas damit zu tun hat, wie „lange“ man an der Feder zieht. Etwas präziser ausgedrückt: Die Feder besitzt eine Ruhelänge. Wie der Name andeutet, ist das die Länge der Feder, wenn du sie in Ruhe lässt. Fängst du an das Federende zu ziehen, änderst du dabei die Ruhelänge. Die Beobachtung, die wir vorhin gemacht haben, bedeutet daher: Je größer die Änderung der Ruhelänge der Feder ist, umso mehr Kraft musst du aufwenden, um die Änderung zu vergrößern.
Änderst du die Ruhelänge einer anderen Feder um den gleichen Betrag, wird sich der Kraftaufwand unterscheiden. Diese Beobachtung fasst man mit Hilfe der Federkonstante zusammen. Wir haben zum Thema Federkonstante einen ausführlichen Beitrag (inklusive Video) zur Verfügung, den du dir bei Interesse gerne anschauen kannst.
Aus diesen zwei Beobachtungen lässt sich ein physikalisches Gesetz formulieren. Ähnliche Beobachtungen machte auch der britische Physiker Robert Hooke. Ihm zur Ehre hat man das Gesetz, das die Beobachtungen von oben zusammenfasst, Hookesches Gesetz genannt. Weiter unten wirst du dazu die Formel finden. Wenn du dich mit diesem Thema etwas mehr beschäftigen möchtest, haben wir auch dazu einen ausführlichen Beitrag, den du durch Anklicken der Verlinkung leicht erreichen kannst.
Hookesches Gesetz
Anhand der Beobachtungen, die wir im vorherigen Abschnitt gemacht haben, lässt sich das Hookesche Gesetz formulieren als
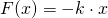 .
.
Das Minuszeichen in der Formel teilt uns mit, dass es sich bei der Spannkraft um eine Rückstellkraft handelt. Das bedeutet einfach ausgedrückt, dass die Feder versucht ihre Ruhelänge beizubehalten. Wenn du die Feder also nach rechts ziehst, wird sie versuchen deine Hand nach links zu ziehen. Wenn du hingegen die Feder nach links drückst, wird sie versuchen deine Hand nach rechts zu drücken.
Federkonstante
Es ist erstaunlich, dass sich die Federkraft beziehungsweise Spannkraft mit einer solch einfachen Formel ausrechnen lässt. Wenn du an einer Feder ziehst, sind die mikroskopischen Reaktionen darauf kompliziert. Möchtest du die Situation auf mikroskopischer Ebene, zum Beispiel mit den Newtonschen Axiomen , verstehen, müsstest du die Bewegung eines jeden Moleküls der Feder berücksichtigen. Würden sich innerhalb der Feder nur zwei oder drei Moleküle befinden, wäre das sogar möglich. Aber es sind nicht nur zwei oder drei, sondern um viele Größenordnungen mehr. Du merkst also, dass die mikroskopische Betrachtung eine sehr mühsame und unpraktische wäre.
Zum Glück reicht für die meisten technischen Anwendungen die makroskopische Ansicht auf die Spannkraft. Je nach Material und Form des Materials kann man der mikroskopischen Reaktion auf eine Änderung der Ruhelänge eine Zahl zuweisen. Und genau diese Information steckt in der Federkonstanten. Das heißt, statt mikroskopisch die Bewegung einer Unzahl an Molekülen zu verfolgen, weist man dem Material für die makroskopische Betrachtung die Federkonstante zu. Die Federkonstante kann beispielsweise durch den Zugversuch bestimmt werden.
Schwingung Feder
Eine typische Anwendung der Spannkraft ist das Federpendel . Von der Umsetzung ist es ähnlich zum Experiment, das wir weiter oben durchgeführt haben. Der Unterschied zum Aufbau steckt darin, dass an das nicht fixierte Federende eine beliebige Masse befestigt wird. Zusätzlich dient das Federpendel nicht zur Beobachtung des Hookeschen Gesetzes, sondern zum Erforschen von harmonischen Schwingungen . Man kann das Federpendel sowohl horizontal betrachten, was der Situation in unserem Experiment oben entspricht, als auch vertikal. Im vertikalen Aufbau muss dabei die Gewichtskraft der hängenden Masse berücksichtigt werden. Wenn du dich mit den Themen in diesem Absatz näher beschäftigen möchtest, dann laden wir dich herzlich dazu ein, auf die Verlinkungen zu klicken. Du wirst dort nicht nur auf einen ausführlichen Beitrag zum entsprechenden Thema stoßen, sondern auch ein animiertes Erklärvideo vorfinden.