Gebrochen rationale Funktionen
Du willst wissen, was gebrochen rationale Funktionen ausmacht? In diesem Artikel erklären wir dir alle wichtigen Eigenschaften, wie beispielsweise den Unterschied zwischen echt und unecht gebrochen rationalen Funktionen. Am Ende findest du eine kurze Zusammenfassung und einige Aufgaben zum selbst Üben.
Du willst lieber Schritt für Schritt sehen, was passiert? Schau dir unser Video an, um gebrochen rationale Funktionen noch besser zu verstehen!
Inhaltsübersicht
Gebrochen rationale Funktionen einfach erklärt
Gebrochen rationale Funktionen wirken mit Blick auf ihre Funktionsgraphen im ersten Moment komplizierter, als sie eigentlich sind. Tatsächlich sind sie nur Brüche, deren Zähler und Nenner jeweils ein Polynom enthält.
![Rendered by QuickLaTeX.com \[f(x)=\cfrac{p(x)}{q(x)}=\cfrac{a_nx^n+\ldots+a_2x^2+a_1x+a_0}{b_mx^m+\ldots+b_2x^2+b_1x+b_0}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b6283e8525d0ef8240c9b346e7abf7a2_l3.png)
Merke: Eine Funktion f(x) nennst du gebrochen rational, wenn ihr Funktionsterm der Quotient zweier Polynome p(x) und q(x) ist.
Je nachdem, wie komplex die Polynome p(x) und q(x) sind, kann deine Funktion die unterschiedlichsten Funktionsgraphen besitzen, die unter dem Begriff Hyperbel zusammengefasst werden.
Arten gebrochen rationaler Funktionen
Gebrochenrationale Funktionen haben die obige allgemeine Funktionsgleichung, aus der du bereits viele Eigenschaften ablesen kannst. Am wichtigsten ist dabei die Klassifizierung nach Zählergrad und Nennergrad. Der Zählergrad ist die höchste Potenz, die im Zähler vorkommt, als Nennergrad bezeichnet man die höchste Potenz des Nenners. Beispielsweise hat die gebrochen rationale Funktion
![Rendered by QuickLaTeX.com \[f(x)=\cfrac{3x^4-x^2-1}{x^6+10x^4-5}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6bb17c2cc61547d3046cb8614a360d5a_l3.png)
den Zählergrad ZG=4 und den Nennergrad NG=6. Daran kannst du bereits erkennen, welcher Art die Asymptoten sind und wie der Funktionsgraph für gebrochenrationale Funktionen im Allgemeinen aussehen muss.
Prinzipiell werden gebrochen rationale Funktionen in zwei verschiedene Arten unterteilt. Es gibt echt gebrochen rationale Funktionen und unecht gebrochen rationale Funktionen. Den genauen Unterschied erklären wir dir jetzt.
Unecht gebrochen rationale Funktionen
Unecht gebrochen rationale Funktionen sind – wie der Name schon sagt – keine echten gebrochenrationalen Funktionen. Sie sehen nur im ersten Moment so aus. Bei genauerer Betrachtung kannst du sie stets so kürzen, dass am Ende keine Funktion mehr im Nenner des Bruches steht, das heißt insbesondere keine Variable x.
- Beispiel 1:
![Rendered by QuickLaTeX.com \[f(x)=\cfrac{x^3}{x} = x^2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f2a77a81d3f72a1dfb178d7065ec329a_l3.png)
- Beispiel 2:
![Rendered by QuickLaTeX.com \[g(x)=\cfrac{x^2-4}{x-2}=\cfrac{(x-2)(x+2)}{(x-2)} = x+2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6d24acb83364ebfe7615a2df3370e4cd_l3.png)
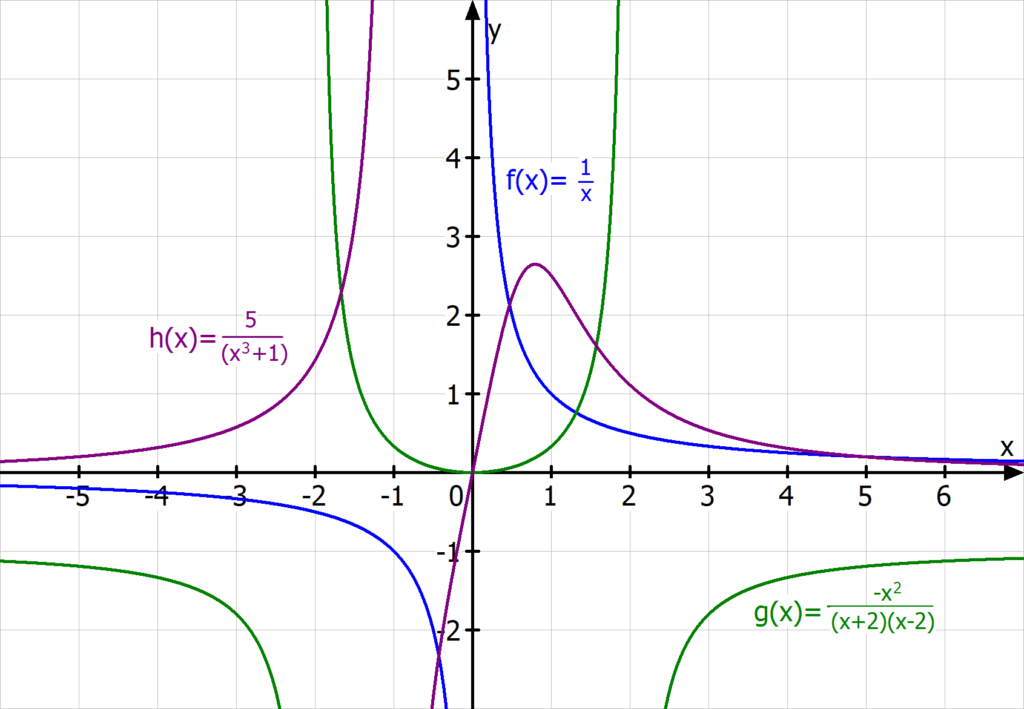
Durch das Kürzen verschwindet der Bruch, sodass du statt gebrochenrationalen Funktionen nur noch eine ganzrationale Funktion betrachtest. In den obigen Beispielen erhältst du eine quadratische Funktion im ersten Fall und eine lineare Funktion im zweiten Fall.
Merke: Für gebrochenrationale Funktionen ist in beiden Fällen bei den Nullstellen des Nenners eine hebbare Definitionslücke gegeben, die nach dem Kürzen nicht mehr erkennbar ist! Sie wird in der Abbildung durch den pinken Kreis veranschaulicht.
Merke: Ist für eine gebrochen rationale Funktion der Zählergrad größer ist als der Nennergrad, so handelt es sich oft um eine unecht gebrochen rationale Funktion! Um zu kürzen musst du jedoch manchmal die binomischen Formeln anwenden oder eine Polynomdivision durchführen!
Echt gebrochen rationale Funktionen
Echt gebrochen rationale Funktionen sind im Gegensatz dazu diejenigen Funktionen, die du auch in obiger Graphik abgebildet siehst. Hier haben der Zähler und der Nenner unterschiedliche Nullstellen und du kannst die Variable x im Nenner nicht kürzen!
- Beispiel 3:
![Rendered by QuickLaTeX.com \[f(x)= \cfrac{1}{x^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ad0db08446af8ee906175d42df5c146b_l3.png)
- Beispiel 4:
![Rendered by QuickLaTeX.com \[g(x)= \cfrac{2x+1}{x^3}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-83edbb23ab2c91309ecba8c50738ca2e_l3.png)
Von diesen Fällen sprechen wir nachfolgend, wenn wir gebrochenrationale Funktionen genauer untersuchen.
Definitionsbereich und Wertebereich
Bekanntermaßen ist das „Durch-Null-Teilen“ in der Mathematik weder erlaubt noch sinnvoll. Daher müssen wir für gebrochenrationale Funktionen 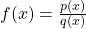 stets die Nullstellen des Nenners aus dem Definitionsbereich
ausschließen. Um den Definitionsbereich zu bestimmen, gehst du somit wie folgt vor:
stets die Nullstellen des Nenners aus dem Definitionsbereich
ausschließen. Um den Definitionsbereich zu bestimmen, gehst du somit wie folgt vor:
-
Schritt 1: Berechne die Nullstellen
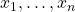 des Nenners
des Nenners
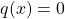
- Schritt 2: Schließe sie aus der Menge der reellen Zahlen aus
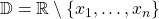
Sowohl bei Beispiel 3 als auch Beispiel 4 aus dem vorigen Abschnitt hat der Nenner eine Nullstelle bei 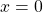 . Somit ist in beiden Fällen der Definitionsbereich
. Somit ist in beiden Fällen der Definitionsbereich 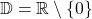 .
.
Betrachten wir dahingegen die Beispiele 1 und 2, so bestimmen wir den Definitionsbereich bevor wir kürzen als 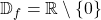 und
und 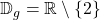 .
.
Merke: Unecht gebrochenrationale Funktionen haben trotzdem Definitionslücken bei den Nullstellen des Nenners, auch wenn du sie im zweiten Schritt kürzen kannst. Hier spricht man auch von sogenannten hebbaren Definitionslücken!
Bei der Bestimmung des Wertebereichs
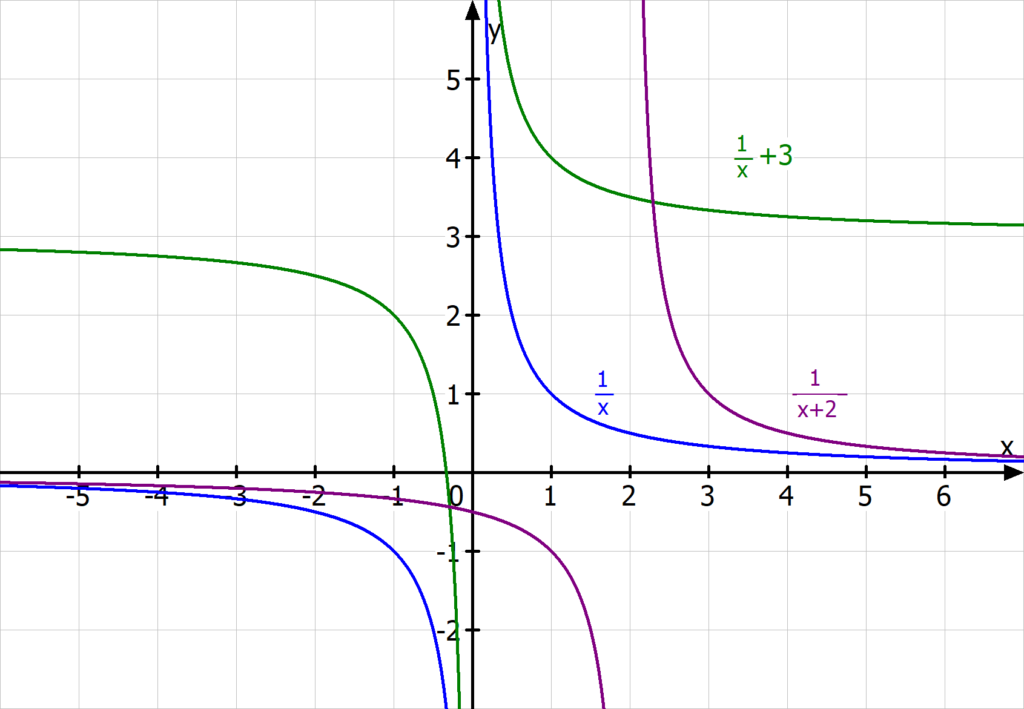
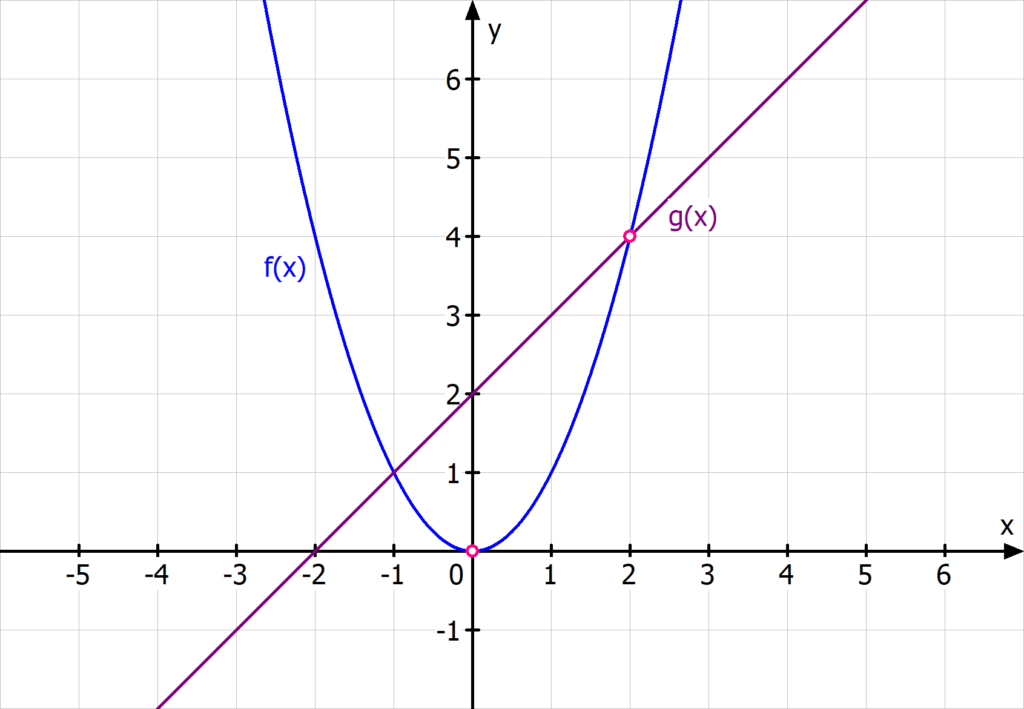
musst du feststellen, welche Werte der Funktionsterm nie annehmen kann. Für verschiedene gebrochen rationale Funktionen gibt es hier unterschiedliche Möglichkeiten. Beispiel 3 (blau) hat den Wertebereich 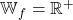 , während der lila Funktionsgraph aus Beispiel 4 den Wertebereich
, während der lila Funktionsgraph aus Beispiel 4 den Wertebereich 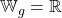 hat.
hat.
Nullstellen und Polstellen
Um herauszufinden, wo der Funktionsgraph die x-Achse schneidet, können wir den Nenner der gebrochenrationalen Funktionen außer Acht lassen. Gebrochen rationale Funktionen 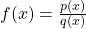 haben ihre Nullstellen stets bei den Nullstellen des Zählers. Um sie zu bestimmen, berechnest du daher
haben ihre Nullstellen stets bei den Nullstellen des Zählers. Um sie zu bestimmen, berechnest du daher
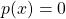 .
.
Von einer Polstelle spricht man dahingegen dann, wenn die Funktion an einer Definitionslücke divergiert, das heißt im Limes gegen unendlich läuft. Hier erhältst du eine senkrechte Asymptote, bei der du noch untersuchen musst, ob es sich um eine Polstelle mit Vorzeichenwechsel (VZW) handelt, oder eine Polstelle ohne Vorzeichenwechsel vorliegt. Dazu setzt du Werte knapp größer beziehungsweise kleiner der Definitionslücke ein und betrachtest das Vorzeichen der Ergebnisse.
Beispielsweise hat 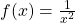 aus Beispiel 3 im Ursprung eine Polstelle ohne Vorzeichenwechsel, da
aus Beispiel 3 im Ursprung eine Polstelle ohne Vorzeichenwechsel, da 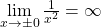 ist. Genaueres dazu erklären wir dir in einem eigenen Artikel „Polstellen
„.
ist. Genaueres dazu erklären wir dir in einem eigenen Artikel „Polstellen
„.
Grenzwertverhalten und Asymptoten
Um für gebrochen rationale Funktionen eine Aussage über das globale Verhalten ableiten zu können, müssen wir eine Grenzwertbetrachtung durchführen. Dazu untersuchen wir den Limes an allen Rändern des Definitionsbereichs.
Insgesamt gibt es drei verschiedene Arten von Asymptoten , die für uns relevant sind. Detailliert findest du sie in einem separaten Artikel erklärt, hier fassen wir nur die wichtigsten Ergebnisse zusammen. Die Asymptoten sind jeweils vom Zählergrad und vom Nennergrad der gebrochenrationalen Funktion festgelegt:
Zählergrad < Nennergrad
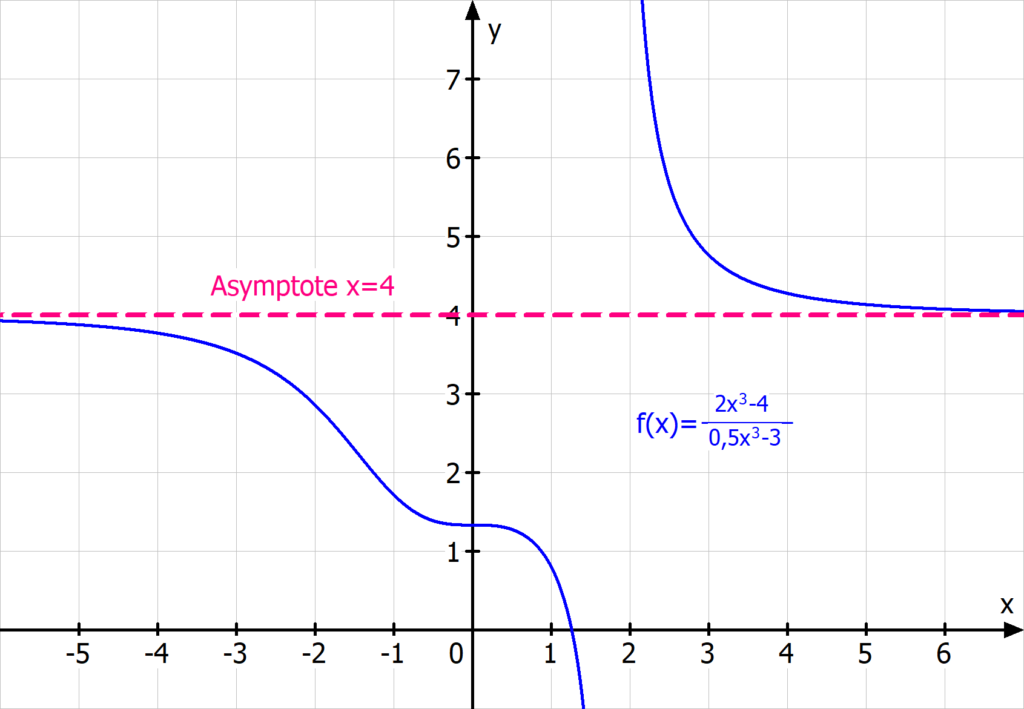
In diesem Fall ist die x-Achse immer eine waagrechte Asymptote, da gilt
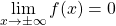 .
.
Die Funktionsgraphen der Beispiele 3 und 4 veranschaulichen dies.
Zählergrad > Nennergrad
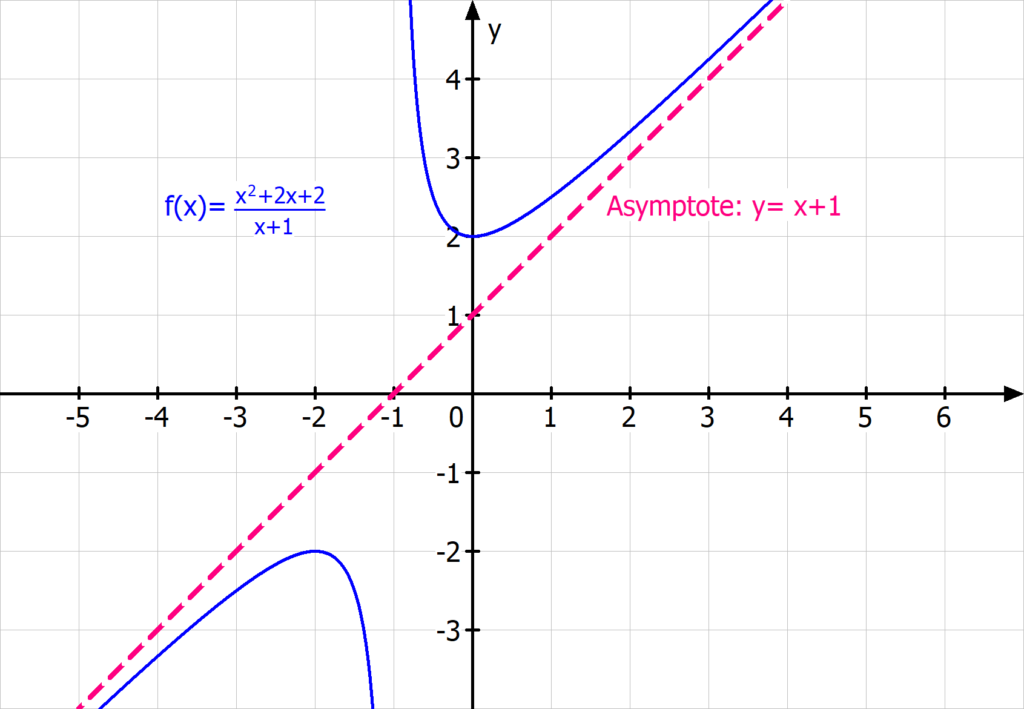
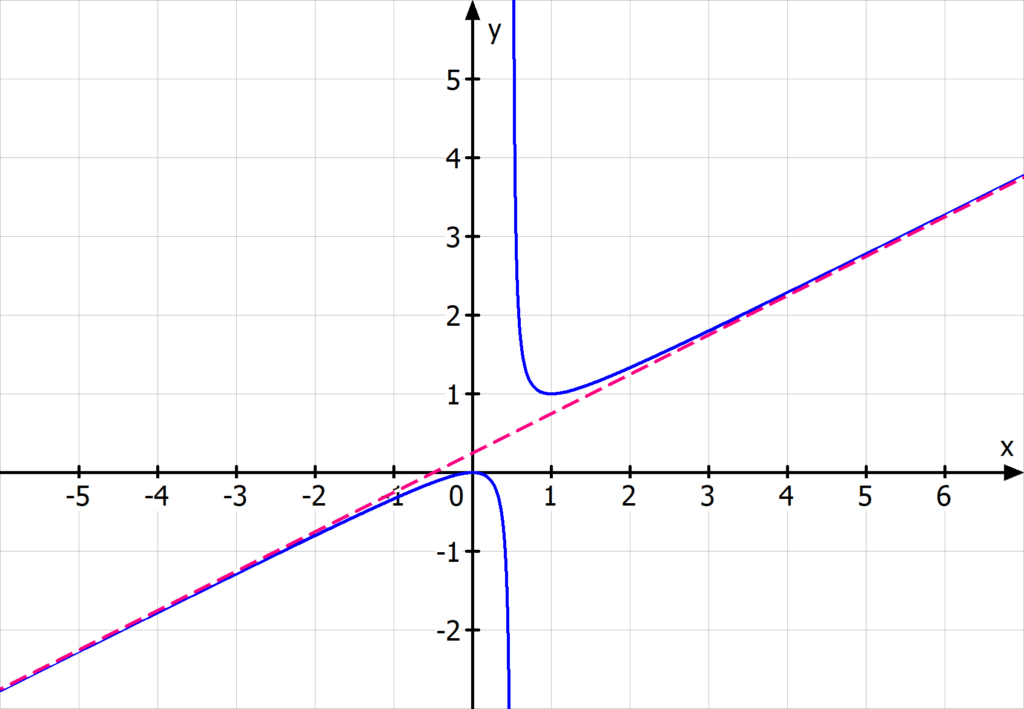
In diesem Fall gibt es keine waagrechte Asymptote, sondern du musst wieder zwei Fälle unterscheiden. Ist dein Zählergrad nur um eins größer als der Nennergrad, das heißt ZG=NG+1, dann erhältst du eine schräge Asymptote. Ihre Geradengleichung kannst du mittels Polynomdivision berechnen.
Angenommen, du willst die schräge Asymptote von der gebrochen rationalen Funktion berechnen
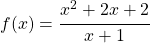 .
.
Dann führst du eine Polynomdivision durch und erhältst
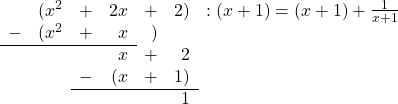
Somit hat deine schräge Asymptote die Funktionsgleichung 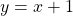 , was du leicht am Funktionsgraphen verifizieren kannst.
, was du leicht am Funktionsgraphen verifizieren kannst.
Ist der Grad des Zählers um mehr als 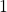 größer als der Nennergrad, so erhältst du eine kompliziertere Funktion, die du aber ebenfalls mit Polynomdivision bestimmen kannst.
größer als der Nennergrad, so erhältst du eine kompliziertere Funktion, die du aber ebenfalls mit Polynomdivision bestimmen kannst.
Gebrochen rationale Funktionen zeichnen
Im Folgenden zeigen wir dir, wie du den Verlauf einer gebrochen rationalen Funktion bestimmen und sie somit zeichnen kannst.
Einfluss von Parametern auf gebrochen rationale Funktionen
Vergleichen wir die Funktionsgleichung 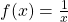 mit ihrer allgemeinsten Form, so kann darauf die Funktion der einzelnen Parameter a, b und c abgeleitet werden.
mit ihrer allgemeinsten Form, so kann darauf die Funktion der einzelnen Parameter a, b und c abgeleitet werden.
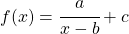
Durch die Addition von c werden gebrochen rationale Funktionen im Koordinatensystem in y-Richtung nach oben beziehungsweise unten verschoben. Der Parameter b bewirkt dahingegen eine Verschiebung in x-Richtung nach links oder rechts. Hat a ein negatives Vorzeichen, so wird der Funktionsgraph an der x-Achse gespiegelt, im Allgemeinen gibt a jedoch die Steilheit der gebrochen rationalen Funktion an.
Schritt für Schritt Anleitung
Um gebrochen rationale Funktionen zu zeichnen, musst du all ihre Eigenschaften berücksichtigen, das heißt sie schrittweise nach den obigen Kriterien untersuchen. Dazu gehst du wie folgt vor, das zugehörige Beispiel findest du im nächsten Abschnitt.
- Schritt 1: Bestimme den Definitionsbereich, also auch die Nullstellen des Nenners.
- Schritt 2: Handelt es sich um eine echt oder eine unecht gebrochenrationale Funktion? Bestimme dies anhand von Zählergrad und Nennergrad. Kürze gegebenenfalls.
- Schritt 3: Untersuche die gebrochen rationale Funktion auf ihre Nullstellen, das heißt die Nullstellen des Zählers.
- Schritt 4: Bestimme die Art der Polstellen, untersuche sie also auf Vorzeichenwechsel etc. Führe dazu eine Grenzwertberechnung an den Definitionslücken durch.
- Schritt 5: Betrachte das Verhalten der gebrochen rationalen Funktion an den äußeren Rändern des Definitionsbereichs und bestimme die Asymptote.
- Schritt 6: Zeichne zuerst die Asymptoten in das Koordinatensystem ein und dann die gebrochen rationale Funktionen unter Berücksichtigung aller Erkenntnisse.
Zusammenfassung: Gebrochen rationale Funktionen
Definitionsbereich Nullstellen des Nenners ausschließen
Wertebereich Asymptote ausschließen
Nullstellen Nullstellen des Zählers berechnen
Polstellen mit oder ohne Vorzeichenwechsel? Grenzwertbetrachtung an den Definitionslücken
Asymptoten
Grenzwertbetrachtung für 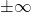
Gebrochen rationale Funktionen Aufgaben
Nun stellen wir dir noch ein paar Aufgaben zu den gebrochen rationalen Funktionen mit Lösungen zum Üben zur Verfügung.
Aufgabe 1: Gebrochen rationale Funktionen – Kurvendiskussion
Gegeben ist die gebrochen rationale Funktion 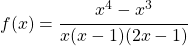 .
.
a) Bestimme den Definitionsbereich. Handelt es sich um eine echt oder unecht gebrochen rationale Funktion?
b) Welche Nullstellen hat die gebrochen rationale Funktion?
c) Untersuche die gebrochenrationale Funktion an ihren Polstellen. Liegen Vorzeichenwechsel vor?
d) Hat die gebrochen rationale Funktion eine Asymptote? Wenn ja, welcher Art?
Aufgabe 2: Gebrochen rationale Funktionen zeichnen
Zeichne die Funktion 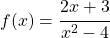 .. Gehe dabei nach der obigen Schritt-für-Schritt-Anleitung vor.
.. Gehe dabei nach der obigen Schritt-für-Schritt-Anleitung vor.
Lösung:
Aufgabe 1: Gebrochenrationale Funktionen – Kurvendiskussion
a) Um den Definitionsbereich für gebrochen rationale Funktionen zu bestimmen, benötigen wir die Nullstellen des Nenners
 .
.
Somit ist 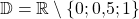 . Dabei hat die gebrochen rationale Funktion eine hebbare Definitionslücke bei
. Dabei hat die gebrochen rationale Funktion eine hebbare Definitionslücke bei 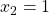 und
und 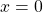 , weil
, weil
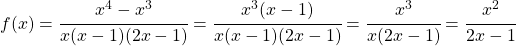
Da trotzdem ein Polynom im Nenner besteht, bleibt die Funktion echt gebrochen rational.
b) Um die Nullstellen der gebrochen rationalen Funktion zu bestimmen, berechnen wir die Nullstelle des Zählers bei
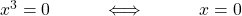
c) Gebrochen rationale Funktionen haben Polstellen an ihren nichthebbaren Definitionslücken. Bei 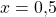 liegt eine Polstelle mit Vorzeichenwechsel vor, da
liegt eine Polstelle mit Vorzeichenwechsel vor, da
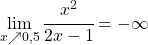
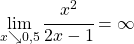
d) Gebrochenrationale Funktionen, deren Zählergrad um 1 größer ist als der Nennergrad, haben stets eine schräge Asymptote. Sie kann durch Polynomdivision berechnet werden.
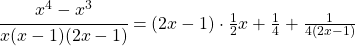
Damit hat die schräge Asymptote die Gleichung 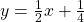 .
.
Aufgabe 2: Gebrochenrationale Funktionen zeichnen
-
Schritt 1: Für gebrochenrationale Funktionen ist der Definitionsbereich
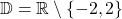 , da
, da

-
Schritt 2: Hier ist der Zählergrad
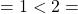 Nennergrad, es handelt sich somit um eine echt gebrochenrationale Funktion.
Nennergrad, es handelt sich somit um eine echt gebrochenrationale Funktion.
- Schritt 3: Die gebrochenrationale Funktionen haben als Nullstellen die Nullstellen des Zählers, das heißt

-
Schritt 4: Um die Polstellen zu bestimmen, betrachten wir das Verhalten der Funktion an den Definitionslücken
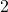 und
und 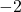 . In beiden Fällen liegt eine Polstelle mit Vorzeichenwechsel vor, da
. In beiden Fällen liegt eine Polstelle mit Vorzeichenwechsel vor, da
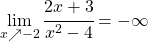
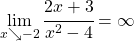
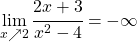
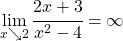
- Schritt 5: Da der Nennergrad größer ist als der Zählergrad ist die x-Achse die waagrechte Asymptote.
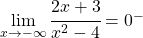
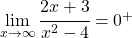
- Schritt 6: Diese gebrochenrationale Funktion hat den folgenden Funktionsgraph:
Exponentialfunktionen
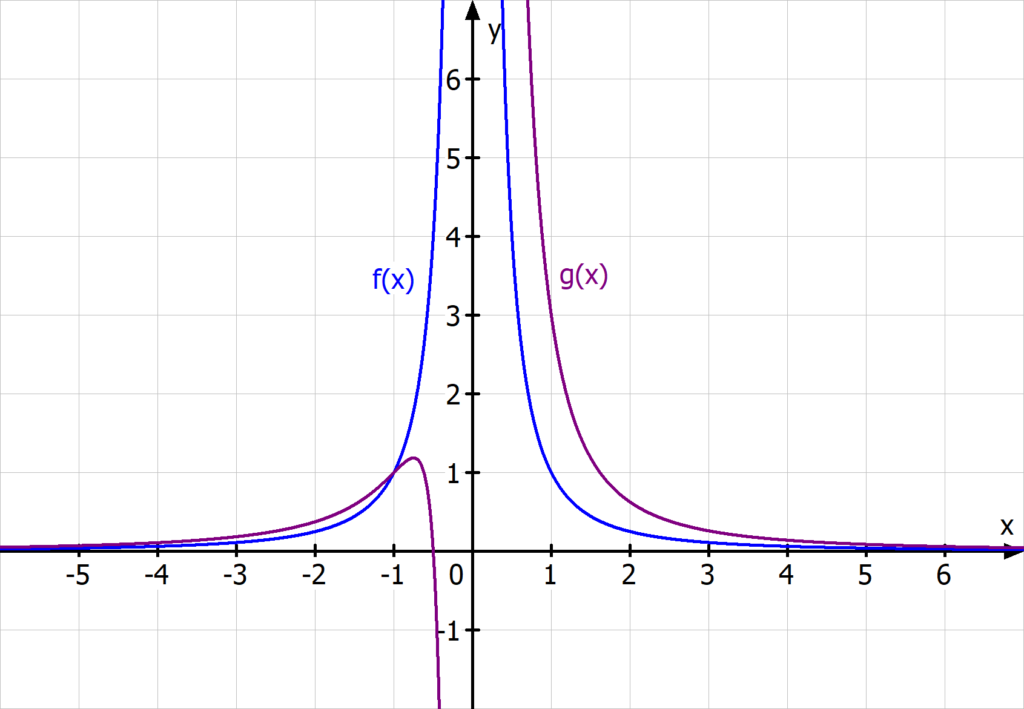
Eine weitere Funktionsart, die du in Mathe sehr häufig brauchst, ist die Exponentialfunktion. Mit der Funktion der Form 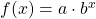 wird exponentielles Wachstum oder Zerfall dargestellt. Alles Wichtige zu den Exponentialfunktionen und ihren Eigenschaften erfährst du in unserem Video
dazu. Schau es dir gleich an!
wird exponentielles Wachstum oder Zerfall dargestellt. Alles Wichtige zu den Exponentialfunktionen und ihren Eigenschaften erfährst du in unserem Video
dazu. Schau es dir gleich an!
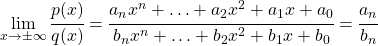 .
.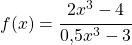 sind die beiden Leitkoeffizienten
sind die beiden Leitkoeffizienten 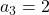 und
und 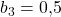 . Damit ist
. Damit ist 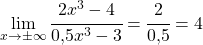 .
.