Potenzreihen
Die Potenzreihen bereiten dir immer noch Probleme? Im Folgenden zeigen wir dir, was es mit den Potenzreihen auf sich hat und wie du ihren Konvergenzradius bestimmen kannst.
Inhaltsübersicht
Potenzreihen Konvergenzradius: Wurzelkriterium
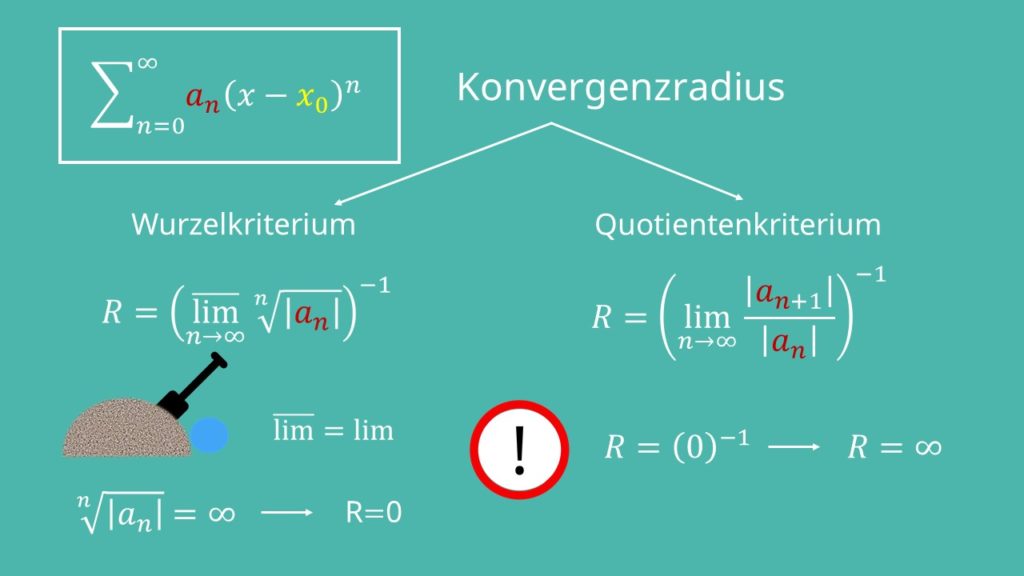
Man definiert den zugehörigen Konvergenzradius entweder über das Wurzelkriterium als:
![Rendered by QuickLaTeX.com R:=\left({\bar{\lim\limits_{n\rightarrow\infty}}}{\sqrt[n]{\left|a_n\right|}}\right)^{-1}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-bfd5d6ae7844388f782bd70af5ca973a_l3.png)
Der Limes Superior ist der größte Häufungspunkt einer Folge und ist bei einer konvergierenden Folge das gleiche wie der Limes. Falls die Folge ![Rendered by QuickLaTeX.com \sqrt[n]{\left|a_n\right|}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-12185c33cfce94011f2d1dfcac0505e5_l3.png) unbeschränkt ist, setzt man
unbeschränkt ist, setzt man 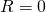 .
.
Potenzreihen Konvergenzradius: Quotientenkriterium
Alternativ kannst du den Konvergenzradius mit dem Quotientenkriterium bestimmen:
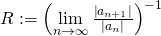
Das Quotientenkriterium darf nur verwendet werden, wenn der Grenzwert tatsächlich existiert. Wenn der Grenzwert in der Klammer Null ist, setzt man formal 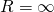 .
.
Man kann beim Quotientenkriterium auch einfach den Grenzwert des Kehrwerts bilden, um den Konvergenzradius zu bestimmen.
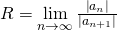
Potenzreihe Konvergenz
Nachdem man den Konvergenzradius ermittelt hat, kann man daher Folgendes über die Konvergenz der Potenzreihe aussagen: Die Potenzreihe ist
- gleichmäßig konvergent auf dem geschlossenen Intervall
![Rendered by QuickLaTeX.com \left[x_0-r,x_0+r\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-95e611301879900b899abc930e8856e8_l3.png) für jedes
für jedes  und
und - divergent für alle x, die weiter von
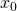 entfernt sind als
entfernt sind als 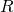
Die Randpunkte 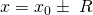 sind kritische Punkte und du musst sie gesondert untersuchen. Die Menge aller x, für die die Potenzreihe konvergiert, heißt Konvergenzbereich
sind kritische Punkte und du musst sie gesondert untersuchen. Die Menge aller x, für die die Potenzreihe konvergiert, heißt Konvergenzbereich 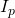 .
.
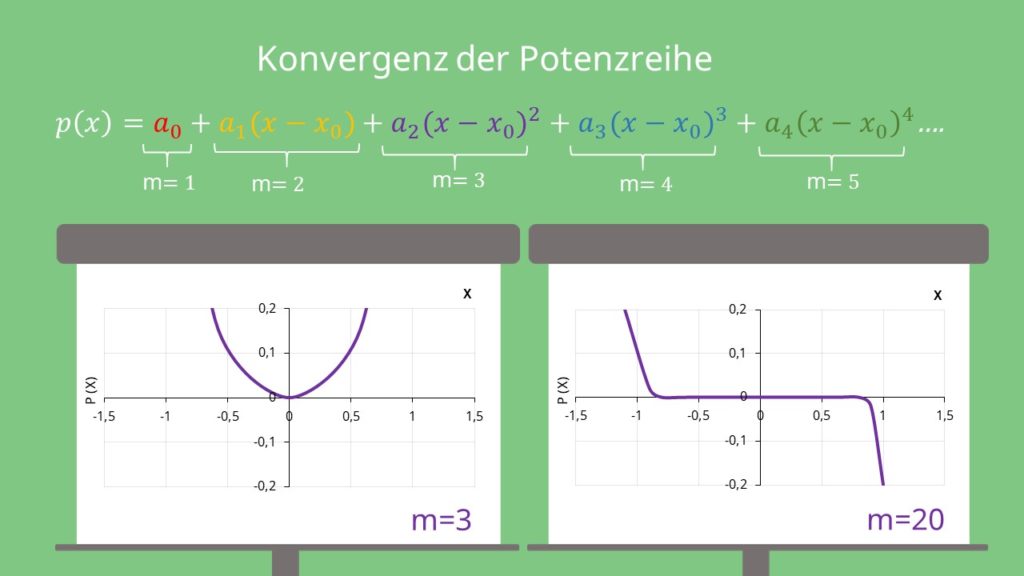
Betrachten wir hierzu noch eine Grafik. Wie aus der Funktionsgleichung erkennbar ist, ist die Potenzreihe für 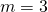 parabelförmig. Mit steigendem
parabelförmig. Mit steigendem 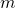 nähert sich die Potenzfunktion
nähert sich die Potenzfunktion 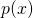 der Form an, die du oben in der Grafik auf der rechten Seite siehst.
der Form an, die du oben in der Grafik auf der rechten Seite siehst.
Eine Potenzreihe ist auf ihrem Konvergenzbereich konvergent, also hat die Reihe hier eine Grenzfunktion, im Beispiel ist diese Null. Dadurch siehst du, dass die Funktion im Bereich zwischen -1 und 1 dagegen konvergiert. Außerhalb des Konvergenzbereichs ist sie divergent. Somit geht die Funktion für Werte größer 1 und kleiner -1 ins Unendliche.
Potenzreihen Beispiele
Sehen wir uns doch an dieser Stelle mal ein Beispiel an:
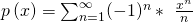
Alternativ könnten wir die Potenzreihe auch so schreiben:
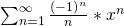
Für diese Potenzreihe p wollen wir den Konvergenzradius bestimmen und nehmen dafür das Quotientenkriterium.
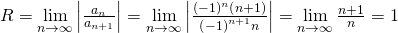
Dann setzen wir 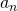 und
und 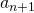 ein. Nach dem umformen sieht der Term folgendermaßen aus. Aufgrund der Betragsstriche fallen die Vorfaktoren
ein. Nach dem umformen sieht der Term folgendermaßen aus. Aufgrund der Betragsstriche fallen die Vorfaktoren 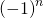 und
und 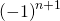 weg. Die Betragsstriche können ebenfalls weggelassen werden. Der Grenzwert ist somit 1. Nun musst du die Randpunkte -1 und 1 untersuchen:
weg. Die Betragsstriche können ebenfalls weggelassen werden. Der Grenzwert ist somit 1. Nun musst du die Randpunkte -1 und 1 untersuchen:
Setze 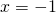 in die Potenzreihe ein und fasse es mit dem anderen Faktor
in die Potenzreihe ein und fasse es mit dem anderen Faktor 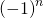 zusammen.
zusammen. 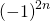 ergibt 1. Es ergibt sich die harmonische Reihe. Die ist bekanntlich divergent. Jetzt musst du noch
ergibt 1. Es ergibt sich die harmonische Reihe. Die ist bekanntlich divergent. Jetzt musst du noch 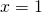 einsetzen.
einsetzen.
Du kannst 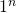 einfach weglassen. Jetzt ziehen wir noch den Vorfaktor -1 aus der Summe, um den Grenzwert besser bestimmen zu können. Es ergibt sich dann die alternierende harmonische Reihe. Diese ist nach dem Leibniz-Kriterium konvergent. Der Grenzwert ist im Beispiel also
einfach weglassen. Jetzt ziehen wir noch den Vorfaktor -1 aus der Summe, um den Grenzwert besser bestimmen zu können. Es ergibt sich dann die alternierende harmonische Reihe. Diese ist nach dem Leibniz-Kriterium konvergent. Der Grenzwert ist im Beispiel also 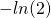 . Die Erkenntnis, dass der Grenzwert existiert, hätte hier allerdings bereits ausgereicht. Den Wert musst du nicht bestimmen.
. Die Erkenntnis, dass der Grenzwert existiert, hätte hier allerdings bereits ausgereicht. Den Wert musst du nicht bestimmen.
Jetzt kannst du den Konvergenzbereich bestimmen, da du weißt, dass die Potenzreihe bei -1 divergiert und bei 1 konvergiert. Der Konvergenzbereich 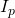 ist also
ist also ![Rendered by QuickLaTeX.com \left(-1,1\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2d50a548eb3807f4c86b2dc5298e3892_l3.png) .
.
Eigenschaften von Potenzreihen
So, zu guter Letzt zeigen wir dir noch ein, zwei praktische Eigenschaften von Potenzreihen.
Für 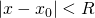 ist die Funktion
ist die Funktion 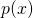 beliebig oft stetig differenzierbar und die Ableitungen können durch gliedweises Differenzieren bestimmt werden.
beliebig oft stetig differenzierbar und die Ableitungen können durch gliedweises Differenzieren bestimmt werden.
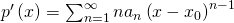
Die erste Ableitung kannst du leicht nachrechnen.
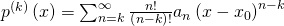
Die k-te Ableitung folgt dem gleichen Schema. Alle Exponenten sind positive ganze Zahlen, daher fallen beim Ableiten Konstanten weg.
Die Konvergenzradien der integrierten oder differenzierten Potenzreihen stimmen mit dem der ursprünglichen Potenzreihe überein.
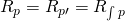
Zusammenfassung Potenzreihen
Fassen wir noch mal zusammen, was du gelernt hast. Du weißt, wie eine Potenzreihe aussieht. Zudem kennst du zwei Wege, den Konvergenzradius zu bestimmen: mit dem Wurzelkriterium und mit dem Quotientenkriterium. Danach hast du gelernt, wie du den Konvergenzbereich bestimmst. Nach diesem Beitrag solltest du keine Probleme mehr mit Potenzreihen haben.