Drallsatz Aufgaben
Du weißt jetzt schon was der Drallsatz ist aber brauchst nochmal ein bisschen Übung vor der nächsten Klausur? Dann bist du hier genau richtig!
Inhaltsübersicht
Berechnung des Drallsatzes
Zu Beginn frischen wir deine Kenntnisse rund um den Drall noch einmal auf: Der Drall bezüglich eines Punktes A wird allgemein gebildet durch:
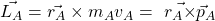
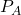 steht hier für den Impuls des Punktes A. Die Formel lässt sich mit Hilfe des Massenträgheitsmoments
steht hier für den Impuls des Punktes A. Die Formel lässt sich mit Hilfe des Massenträgheitsmoments 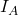 umschreiben. Dieses wird gebildet durch:
umschreiben. Dieses wird gebildet durch:
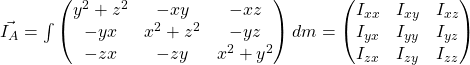
Um uns ein wenig Arbeit zu ersparen, schreiben wir die Koeffizienten der Matrix direkt um.
Dadurch lässt sich der Drall bezüglich des Punktes A umschreiben als
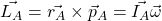
Nachdem wir den Drall noch einmal allgemein aufgestellt haben, betrachten wir als nächstes den Drallsatz. Dieser ist, bezüglich eines Punktes A, definiert durch:
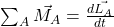
Da wir uns nicht zwangsläufig im Schwerpunkt befinden, bilden wir die Ableitung mit Hilfe des Kreuzproduktes und erhalten:
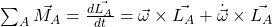
Beispiel Rotor
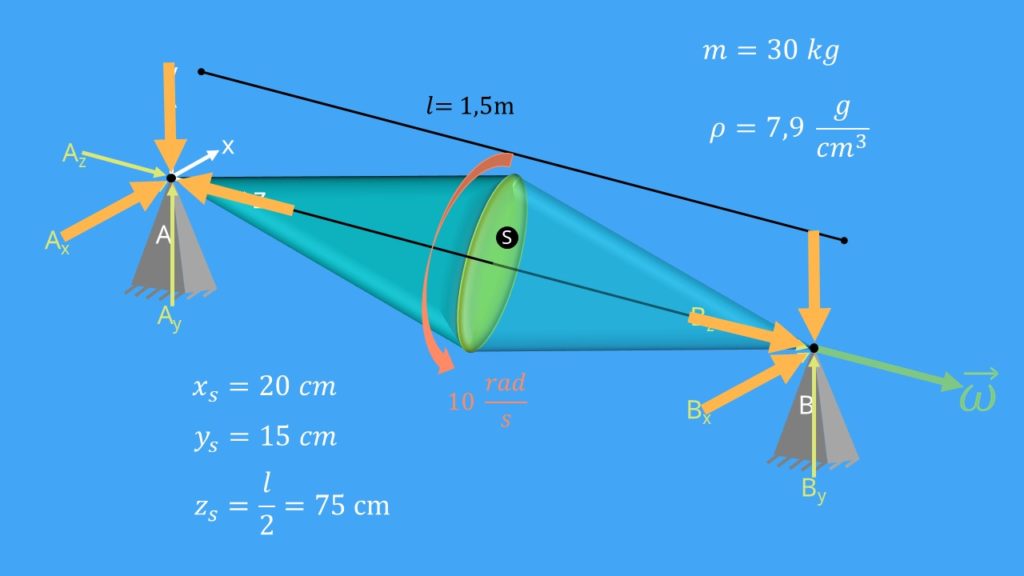
So, damit haben wir die Grundlagen des Drallsatzes noch einmal aufgefrischt. Betrachten wir nun als Beispiel einen Rotor. Den Rotor kannst du dir als zwei Kegel vorstellen, die an der Grundfläche miteinander verbunden sind. Der Rotor selbst wird an den beiden Enden durch zwei Festlager A und B gehalten. Beide Lager können dementsprechend Kräfte in x-, y-, und z-Richtung aufnehmen. Nun sagt der Name Rotor schon, dass dieser sich mit einer Winkelgeschwindigkeit Omega  drehen muss. Dabei liegt die Drehachse auf der Achse, die die beiden Festlager verbindet und hat den Betrag 10 Radiant pro Sekunde. Das Koordinatensystem legen wir uns hier in das Lager A. Dabei ziehen wir die z-Achse durch den Rotor hindurch, sodass Omega genau in z-Richtung zeigt.
drehen muss. Dabei liegt die Drehachse auf der Achse, die die beiden Festlager verbindet und hat den Betrag 10 Radiant pro Sekunde. Das Koordinatensystem legen wir uns hier in das Lager A. Dabei ziehen wir die z-Achse durch den Rotor hindurch, sodass Omega genau in z-Richtung zeigt.
Die y-Achse verläuft senkrecht nach oben und die x-Achse senkrecht zu den beiden Achsen nach hinten. Der Abstand der beiden Festlager, und somit auch die Länge des Rotors, ist L gleich 1,5 m. Der betrachtete Rotor hat jetzt durch einen Produktionsfehler die Schwerpunktkoordinaten 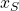 gleich
gleich 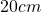 und
und 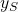 gleich
gleich 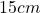 . Der Schwerpunkt in z-Richtung liegt dabei genau in der Mitte. Damit ist
. Der Schwerpunkt in z-Richtung liegt dabei genau in der Mitte. Damit ist 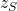 gleich
gleich 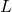 halbe. Weiterhin wissen wir, dass der Rotor die Masse
halbe. Weiterhin wissen wir, dass der Rotor die Masse 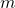 gleich 30kg und eine konstante Dichte Roh gleich 7,9 g pro cm³ besitzt.
gleich 30kg und eine konstante Dichte Roh gleich 7,9 g pro cm³ besitzt.
Auflagerkräfte bestimmen
Dadurch, dass die Schwerpunktkoordinaten 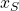 und
und 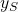 ungleich Null sind, müssen die Auflager Kräfte aufnehmen. Diese wollen wir im Folgenden herausfinden.
ungleich Null sind, müssen die Auflager Kräfte aufnehmen. Diese wollen wir im Folgenden herausfinden.
Zu Beginn widmen wir uns den z-Komponenten: Wenn du die Bewegung allgemein betrachtest, merkst du schnell, dass wir keine Kraft bzw. Bewegung in z-Richtung haben. Wir können also von Anfang an sagen, dass die z-Komponenten der Auflagerkräfte gleich Null sind. Wir suchen somit also nur noch die Kraftkomponenten in x-und y-Richtung. Die Kräfte in den Lagern A und B ergeben sich dann zu:
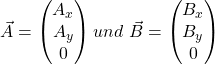
Im nächsten Schritt verwenden wir den Drallsatz. Wie du sicher weißt, ist der Drall ortsabhängig. Bevor wir rechnen, müssen wir also einen Punkt aussuchen, für den wir den Drall bestimmen. Wir wählen hier das Auflager A. Genauso gut könnten wir uns für jeden anderen Punkt, z.B. für Auflager B entscheiden. Den Drall stellen wir mit Hilfe des Massenträgheitsmoments auf. Da Omega nur eine z-Komponente hat, betrachten wir nur diese. Das geht auch aus der Formel für den Drall hervor:
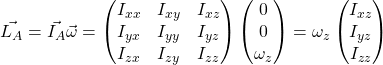
Als nächstes leiten wir den Drall ab.