Dynamik des starren Körpers – Lagrange’sche Gleichung
Du willst wissen auf was man die Lagrange Gleichung in der Mechanik anwenden kann? Genau das zeigen wir dir in diesem Beitrag
Inhaltsübersicht
Bewegungsgleichung mit der Lagrange’schen Gleichung
Wie du aus den letzten beiden Videos bereits weißt, gibt es bei der Betrachtung der Dynamik von starren Körpern zwei Möglichkeiten die Bewegungsgleichung aufzustellen: das Prinzip der virtuellen Verrückung und die Lagrange’sche Gleichung.
Bei Lagrange muss, wie beim Prinzip der virtuellen Verrückung, das System zunächst parametrisiert werden. Anschließend können wir die Gleichung für jeden Parameter anwenden. Wir erhalten sie aus dem Prinzip der virtuellen Verrückung. Sie lautet:
![Rendered by QuickLaTeX.com \phi_i=-\frac{d}{dt}\left[\frac{\partial L}{\partial\dot{q_i}}\right]+\frac{\partial L}{\partial q_i}+Q_i=0](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b8c8e1ea5955ef6c81adbf35b16d5c87_l3.png)
L ist dabei die Lagrangefunktion mit:
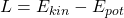
Und das kleine qi ist der betrachtete Parameter.
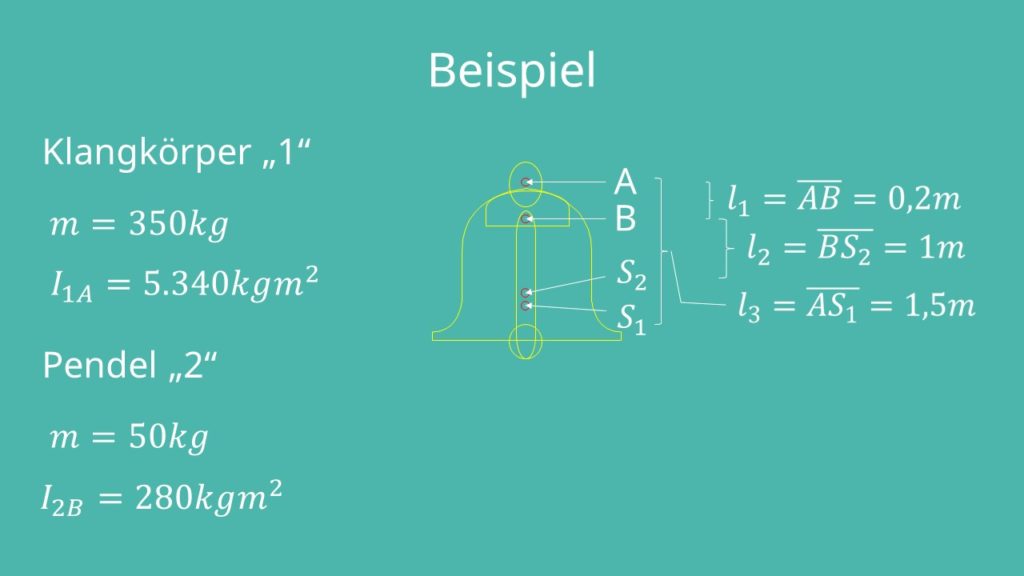
Beispiel Glocke
Nachdem wir die Grundlagen nochmal geklärt haben, wenden wir uns einem Beispiel zu und versuchen die Differentialgleichungen des Systems zu bestimmen. Dafür betrachten wir die Bewegung einer Glocke. Um uns ein wenig Arbeit zu ersparen, nennen wir den Klangkörper Körper eins und das Pendel Körper zwei. Ihr Klangkörper wiegt 350kg und hat ein Massenträgheitsmoment bezüglich A 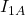 von 5340kg
von 5340kg . Das Pendel wiegt 50kg und hat ein Massenträgheitsmoment bezüglich B
. Das Pendel wiegt 50kg und hat ein Massenträgheitsmoment bezüglich B 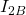 von 280kg
von 280kg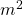 .
.
Das heißt, wir kennen die Trägheitsmomente bezüglich ihrer jeweiligen Aufhängung. Zusätzlich nehmen wir noch an, dass die Bindungen perfekt sind und unser Qi in der Lagrangegleichung gleich Null wird. Das gilt sowohl für die Bindung zwischen Pendel und Klangkörper an Punkt B, als auch für die Bindung des Klangkörpers an der Aufhängung an Punkt A. Weiterhin kennen wir den Schwerpunkt des Klangkörpers S1 und des Pendels S2, und auch den Abstand der Aufhängung zur Bindung:
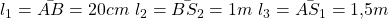
Das Koordinatensystem legen wir genau in den Punkt A mit der x-Achse positiv nach rechts und der y-Achse positiv nach unten.
Um die Differentialgleichungen zu bestimmen, parametrisieren wir das System. Dafür betrachten wir den Ausschlag Phi 1 des Klangkörpers und den Ausschlag des Pendels phi 2. Beide Winkel sind im Verhältnis zur y-Achse angenommen. Wir haben also als Parameter:
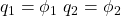
Aufstellen der Lagrangefunktion
Als nächstes müssen wir die Lagrangefunktion aufstellen. Dafür benötigen wir die kinetische und die potentielle Energie . Da der Klangkörper und das Pendel als einzelne Systeme angesehen werden können, betrachten wir die Energien der Systeme zunächst einzeln und addieren diese anschließend. Zunächst schauen wir uns die kinetische Energie an und wenden uns als erstes dem Klangkörper zu. Dafür betrachten wir vorher nochmal die allgemeine Definition der kinetischen Energie des starren Körpers. Diese lautet:
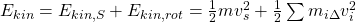
Da der Klangkörper nur eine rotierende Bewegung beschreibt, müssen wir den zweiten Term betrachten. Dieser ist aber so nicht einfach lösbar. Dementsprechend machen wir das gleiche wie beim Drallsatz und stellen uns die Massenpunkte infinitesimal klein vor, um ein Integral bilden zu können. Du kannst dir sicher denken, dass das wieder auf das Massenträgheitsmoment hinausläuft, indem wir, mit Hilfe von Omega, delta v umschreiben.