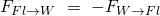Impulssatz
Mit dem Impulssatz in der Strömungsmechanik kannst du einen Erhaltungssatz über ein strömendes Fluid aufstellen. Wie du diesen Impulssatz über ein abgeschlossenes Kontrollvolumen herleiten kannst, zeigen wir dir hier Schritt für Schritt. Wie du den Erhaltungssatz anwenden kannst und wie du damit sogar Oberflächenkräfte bestimmen kannst, zeigen wir dir in einem ausführlichen Beispiel.
Schau dir unser Video zum Impulssatz an! In diesem erklären wir dir den Impulssatz anschaulich und leicht verständlich mit Bild und Ton.
Inhaltsübersicht
Impulssatz einfach erklärt
Der Impulssatz der Strömungslehre ist die Erhaltungsgleichung des Impulses eines strömenden Fluids. Er beschreibt das Kräftegleichgewicht zwischen Fluid und Körper nach dem Prinzip actio=reactio und basiert damit auf dem zweiten newtonschen Axiom.
Impulssatz Herleitung
Die Ursache der Kraft eines Fluids auf Körper hat physikalische Ursprünge. Stellt man sich einen Gartenschlauch vor, der an einer Stelle gekrümmt ist, wird das Wasser in ihm umgelenkt. Durch die Umlenkung dieser kontinuierlichen Strömung wird eine konstante Kraft erzeugt. Die Größe der Kraft kann mit dem Impulssatz der Strömungslehre bestimmt werden.
Herleitung durch das zweite newtonsche Axiom
Der Ausgangspunkt für die Herleitung des Impulssatzes bildet das zweite newtonsche Axiom beziehungsweise Grundgesetz der Dynamik:
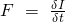
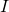 ist dabei der Impuls. Diese Formel sagt aus, dass die Änderung der Bewegungsgröße „Impuls pro Zeit“ einer Kraft entspricht. Anders ausgedrückt: Die Kraft führt zu einer Impulsänderung pro Zeit.
ist dabei der Impuls. Diese Formel sagt aus, dass die Änderung der Bewegungsgröße „Impuls pro Zeit“ einer Kraft entspricht. Anders ausgedrückt: Die Kraft führt zu einer Impulsänderung pro Zeit.
Die Formel für den Impuls einer Einzelmasse ist bereits aus dem Physikunterricht bekannt. Sie lautet:
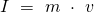
Der Impuls ist eine vektorielle Größe mit der Richtung der Geschwindigkeit, also das Produkt aus seiner Masse 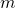 und der Geschwindigkeit
und der Geschwindigkeit  . Für den Impuls bei Flüssigkeiten betrachtet man ein kleines Fluidteilchen mit dem Volumen
. Für den Impuls bei Flüssigkeiten betrachtet man ein kleines Fluidteilchen mit dem Volumen 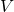 . Da die Masse sich durch das Produkt aus Dichte und Volumen beschreiben lässt, kann Sie in der Formel durch den Ausdruck
. Da die Masse sich durch das Produkt aus Dichte und Volumen beschreiben lässt, kann Sie in der Formel durch den Ausdruck 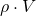 ersetzt werden:
ersetzt werden:
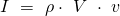
Der Impuls für Flüssigkeiten sei nun Ausgangspunkt der Herleitung des Impulssatzes in der Strömungslehre.
Impulssatz Strömung in einem Kontrollvolumen
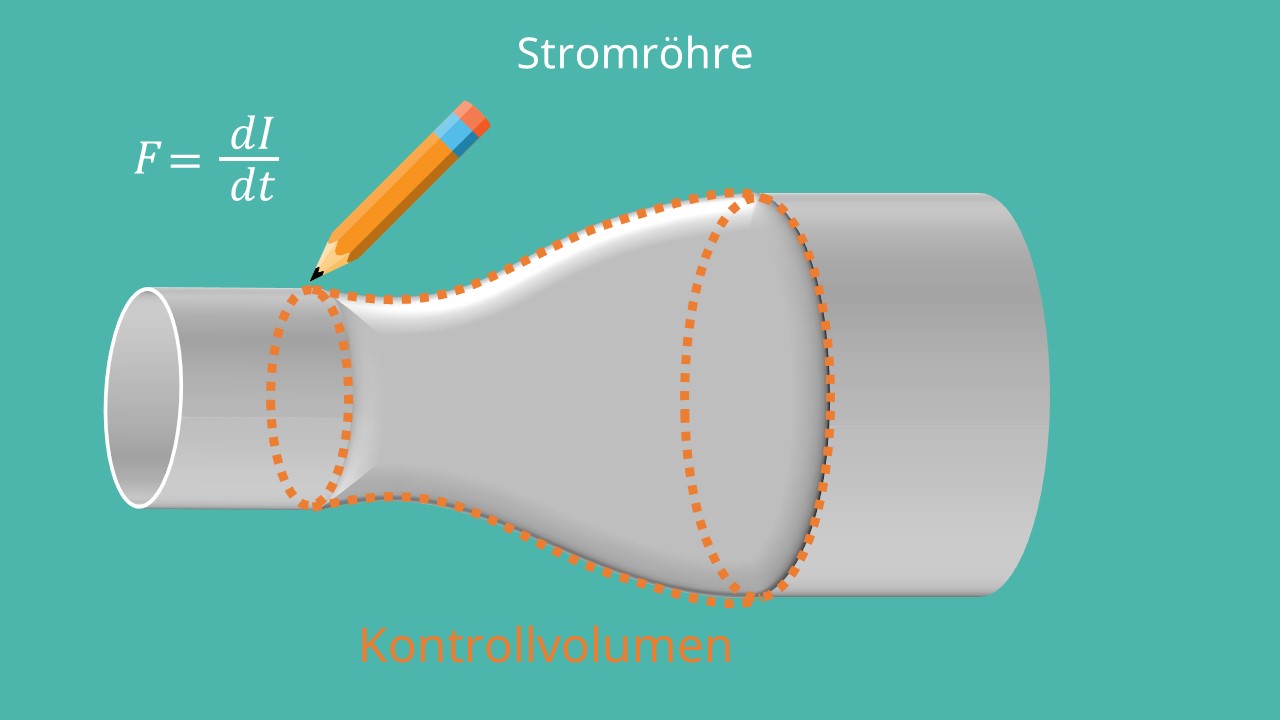
Gegeben sei eine Stromröhre, die sich zum Ende hin zunehmend weitet. Die orangefarbene Linie ist das Kontrollvolumen. Das Kontrollvolumen ist der Bereich, der für die Herleitung des Impulssatzes von Interesse ist und dementsprechend auch definiert sein muss. Im vorangegangenen Kapitel wurde festgelegt, dass die zeitliche Impulsänderung einer Kraft entspricht. Diese Kraft ergibt sich aus den Oberflächenkräften auf das betrachtete Kontrollvolumen des Fluides. Die Oberflächenkräfte wiederum lassen sich mit den Strömungsgrößen berechnen. Diese Stromgrößen können zusätzlich in die Grafik gezeichnet werden.
Links kann die Geschwindigkeit 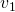 , die das Fluid beim Eintritt in das Kontrollvolumen hat, eingezeichnet werden. Außerdem sind die Fläche
, die das Fluid beim Eintritt in das Kontrollvolumen hat, eingezeichnet werden. Außerdem sind die Fläche 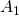 und der Druck
und der Druck 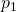 eine wichtige Strömungsgröße. Simultan können beim Austritt die Größen
eine wichtige Strömungsgröße. Simultan können beim Austritt die Größen 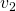 ,
, 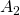 und
und 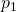 vermerkt werden. Auch tangential entlang der Wand des Kontrollvolumens kann die Geschwindigkeit
vermerkt werden. Auch tangential entlang der Wand des Kontrollvolumens kann die Geschwindigkeit 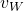 eingetragen werden, darüber hinaus die Fläche
eingetragen werden, darüber hinaus die Fläche 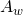 sowie der Druck
sowie der Druck 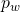 . Letztlich müssen noch die Normalenvektoren eingetragen werden. Sie stehen senkrecht zu den Ein- und Austrittsflächen, sowie senkrecht auf dem Geschwindigkeitsvektor
. Letztlich müssen noch die Normalenvektoren eingetragen werden. Sie stehen senkrecht zu den Ein- und Austrittsflächen, sowie senkrecht auf dem Geschwindigkeitsvektor 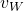 .
.
Impulssatz Berechnung der Oberflächenkräfte
Die Oberflächenkräfte sind alle Kräfte, die auf das Kontrollvolumen einwirken. Ein Druck erzeugt auf eine Fläche immer auch eine entsprechende Kraft, da 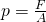 ist. Im Beispiel des Kontrollvolumens lassen sich die Kräfte auf die einzelnen Flächen wie folgt schreiben.
ist. Im Beispiel des Kontrollvolumens lassen sich die Kräfte auf die einzelnen Flächen wie folgt schreiben.
Kraft auf die Oberfläche am Eintritt:
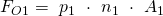
Kraft auf die Oberfläche am Austritt:
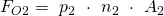
Kraft auf die Wand des Kontrollvolumens:
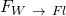
Der Normalenvektor muss wegen der Korrektur der Vorzeichen mit einbezogen werden.
Zeigt 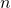 in Bewegungsrichtung des Fluides, also vom Eintritt in Richtung Austritt, dann ist
in Bewegungsrichtung des Fluides, also vom Eintritt in Richtung Austritt, dann ist 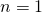 . Im umgekehrten Fall ist
. Im umgekehrten Fall ist 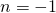 .
.
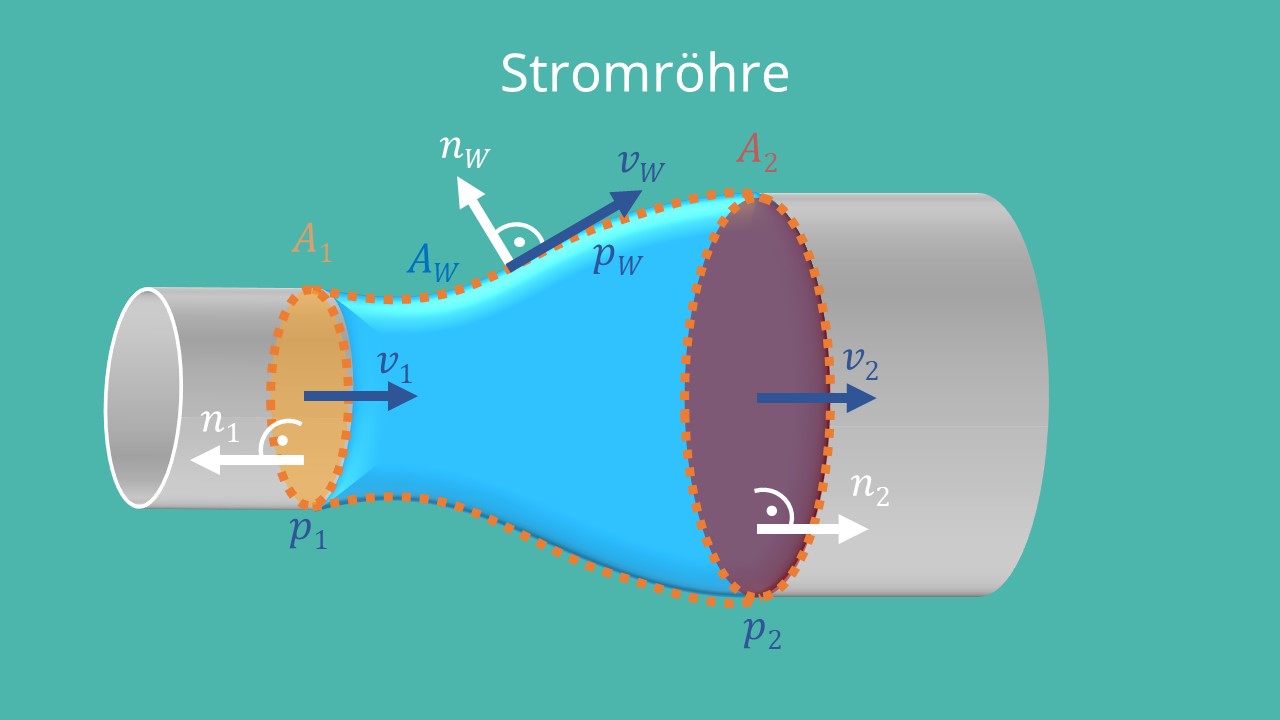
Wie anfangs festgehalten, ist nach dem zweiten newtonschen Axiom die Kraft gleich der Impulsänderung pro Zeit.
Da sich die Kraft durch die Summe der Oberflächenkräfte beschreiben lässt, kann alternativ auch
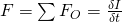
geschrieben werden. Die Summe der Oberflächenkräfte ergibt sich zu:
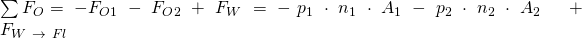
Damit:
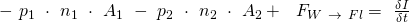
Dabei haben 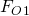 und
und 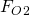 ein anderes Vorzeichen als
ein anderes Vorzeichen als 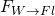 . Dies rührt daher, dass sie die Kraft vom Fluid auf die Wand und nicht die Kraft der Wand auf das Fluid darstellen.
. Dies rührt daher, dass sie die Kraft vom Fluid auf die Wand und nicht die Kraft der Wand auf das Fluid darstellen.
Der Impuls bei Flüssigkeiten ist durch 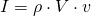 definiert.
definiert.
Somit ist
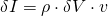 . Mit
. Mit 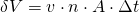
ergibt sich für den Gesamtimpuls:
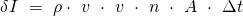
Die Summe der Einzelimpulse ist also:
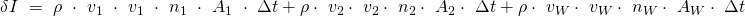
Da 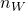 senkrecht auf
senkrecht auf 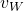 steht, ist das Produkt der beiden Null, womit der letzte Term der Gleichung wegfällt. Anschließend wird das
steht, ist das Produkt der beiden Null, womit der letzte Term der Gleichung wegfällt. Anschließend wird das 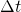 ausgeklammert und
ausgeklammert und 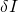 kann in die Gleichung
kann in die Gleichung 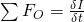 eingesetzt werden:
eingesetzt werden:
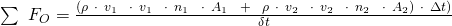
Da 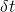 und
und 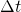 gleichzusetzen ist, kann gekürzt werden, wodurch die Gleichung lautet:
gleichzusetzen ist, kann gekürzt werden, wodurch die Gleichung lautet:
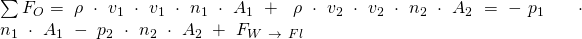
Die Kraft des Fluides kann letztlich berechnet werden, indem die Gleichung nach
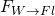
umgestellt wird. Die Kraft des Fluids auf die Wand ergibt sich durch Multiplikation mit -1.