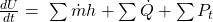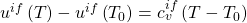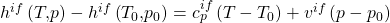Energiebilanz – Übung
In diesem Beitrag erklären wir die die kalorischen Zustandsgleichungen anhand eines Beispiels noch einmal schrittweise.
Inhaltsübersicht
Energiebilanz berechnen
Wenn du viel Bier trinkst, nimmst du normalerweise zu. Doch was ist, wenn du das Bier soweit runter kühlst, dass du die zugenommene Energie beim Aufwärmen wieder verbrauchst? Das wollen wir jetzt herausfinden.
Um zu klären, ob eine solche „Bierdiät“ möglich ist, benötigen wir die Energiebilanz und die kalorischen Zustandsgleichungen der idealen Flüssigkeit.
Energiebilanz Biertrinker
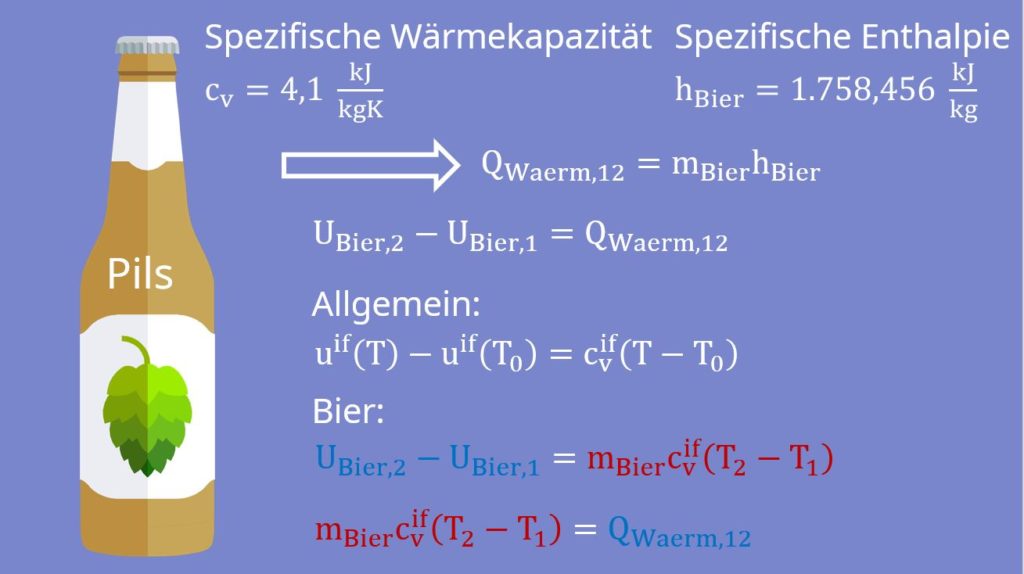
Jetzt benötigen wir noch die spezifischen Werte von Bier. Ein normales Pils hat eine spezifische Wärmekapazität von 4,1 Kilojoule pro Kilogramm Kelvin und eine spezifische Enthalpie von 1758,456 Kilojoule pro Kilogramm bei 37 Grad Celsius, also der Temperatur des Körpers. Um herauszufinden, ob die „Bierdiät“ denn möglich ist, berechnen wir uns die Temperatur, auf die das Bier runter gekühlt werden muss.
Wir beginnen mit der Bilanz um den Biertrinker. Dieser verrichtet natürlich keine technische Arbeit, nimmt aber Energie durch das Bier auf. Dabei erwärmt er das Bier und gibt einen konstanten Wärmestrom ab.
Das intergieren wir jetzt und erhalten:
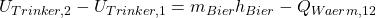
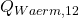 ist die geflossene Wärme, zwischen Zustand eins, also dem Bier bei der gesuchten Temperatur, und Zustand zwei, also der Körpertemperatur.
ist die geflossene Wärme, zwischen Zustand eins, also dem Bier bei der gesuchten Temperatur, und Zustand zwei, also der Körpertemperatur.
Da sich die innere Energie des Trinkers nicht erhöhen soll, muss die Differenz natürlich gleich null sein.
Stellen wir das jetzt nach Q um, erhalten wir:
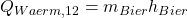
Energiebilanz Bier
Jetzt kennen wir 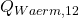 natürlich noch nicht. Dafür machen wir eine Energiebilanz um das Bier herum. Dabei ist die Masse des Biers natürlich konstant und es wird wieder keine technische Arbeit verrichtet:
natürlich noch nicht. Dafür machen wir eine Energiebilanz um das Bier herum. Dabei ist die Masse des Biers natürlich konstant und es wird wieder keine technische Arbeit verrichtet:
Nach der Integration ergibt sich:
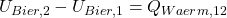
Die Differenz der inneren Energien bekommen wir nun aus dem Stoffmodel der idealen Flüssigkeit:
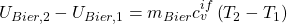
Das können wir jetzt in die Bilanz um das Bier einsetzen:
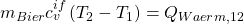
Da 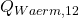 jetzt genau der gleiche Wärmestrom ist, der vom Biertrinker kommt, können wir die erhaltenen Gleichungen gleichsetzen:
jetzt genau der gleiche Wärmestrom ist, der vom Biertrinker kommt, können wir die erhaltenen Gleichungen gleichsetzen:
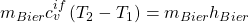
Wir können jetzt die Masse des Bieres kürzen und kennen die Temperatur 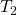 . Diese ist nämlich genau die Temperatur des Körpers mit 37 Grad Celsius. Das heißt, wir müssen es nur nach
. Diese ist nämlich genau die Temperatur des Körpers mit 37 Grad Celsius. Das heißt, wir müssen es nur nach 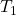 umstellen und erhalten:
umstellen und erhalten:
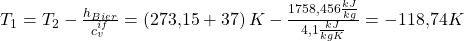
Du erkennst vielleicht, dass das Ergebnis physikalisch nicht sinnvoll ist, da der absolute Nullpunkt ja bei 0 Kelvin definiert ist. Lass dich davon aber nicht irritieren, wir betrachten das Ergebnis als theoretischen Wert, haben die Aufgabe damit gelöst und wissen nun, dass wir die Energie nicht wieder verbrauchen können, die wir beim Biertrinken zu uns nehmen!
Damit haben wir die Energiebilanz Physik abgehakt und sicherlich bist du nun voller Energie für deine nächste Klausur zum Thema Enthalpie und innere Energie.