Berechnung Kreisprozesse
Den Begriff des Verbrennungskraftmotors hast du bestimmt schon einmal gehört. Wir zeigen dir, wie die Energieumwandlung in so einem Motor stattfindet.
Inhaltsübersicht
Die vier Schritte eines Verbrennungsmotors
Damit sich dein Auto in Bewegung setzt, müssen wir beim Verbrennungsmotor natürlich keine Wärme erzielen, sondern Leistung. Also wird unser Prozess rechtsläufig sein. Wenn du wissen willst, was das heißt, dann schau dir am besten das vorherige Video zur Energieumwandlung bei Gasturbinen an. Eine Art eines Verbrennungsmotors ist der Otto-Motor. Diesen wollen wir uns jetzt genauer anschauen.
Wir kennen die spezifische Gaskonstante von Luft:
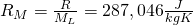
Isotrope Verdichtung
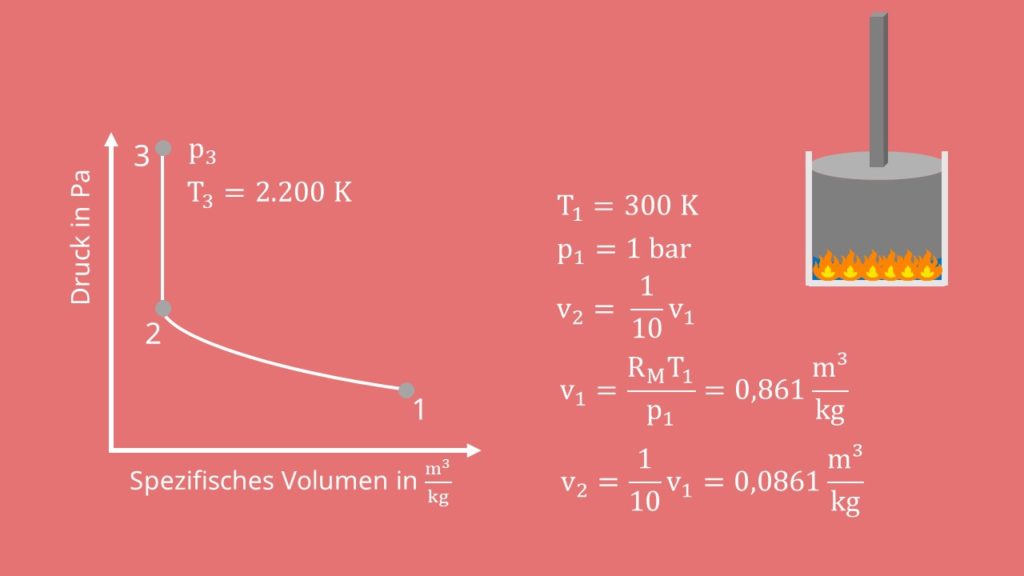
Allgemein machen wir beim idealen Zweitakt-Ottomotor vier Schritte: Wir beginnen mit einer isentropen Verdichtung von Zustand eins mit Temperatur T eins gleich 300 Kelvin, Druck 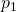 gleich ein bar auf den Zustand zwei mit nur einem Zehntel des spezifischen Volumens von Zustand eins. Das heißt der Kolben presst das Volumen zusammen. Über das ideale Gasgesetz berechnen wir uns das spezifische Volumen
gleich ein bar auf den Zustand zwei mit nur einem Zehntel des spezifischen Volumens von Zustand eins. Das heißt der Kolben presst das Volumen zusammen. Über das ideale Gasgesetz berechnen wir uns das spezifische Volumen 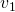 :
:
Als nächstes folgt eine isochore Wärmezufuhr. Hier wird das Benzin verbrannt, während der Kolben an der gleichen Position bleibt. Wir halten das Volumen konstant und erhöhen den Druck auf p drei mit der Temperatur T drei gleich 2200 Kelvin. Wir können uns dann den Druck wieder mit dem idealen Gas berechnen. Mit konstanter Masse und konstantem Volumen 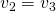 erhalten wir:
erhalten wir:
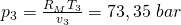
Hier haben wir dann den höchsten Druck innerhalb des Kolbens.
Isentrope Expansion
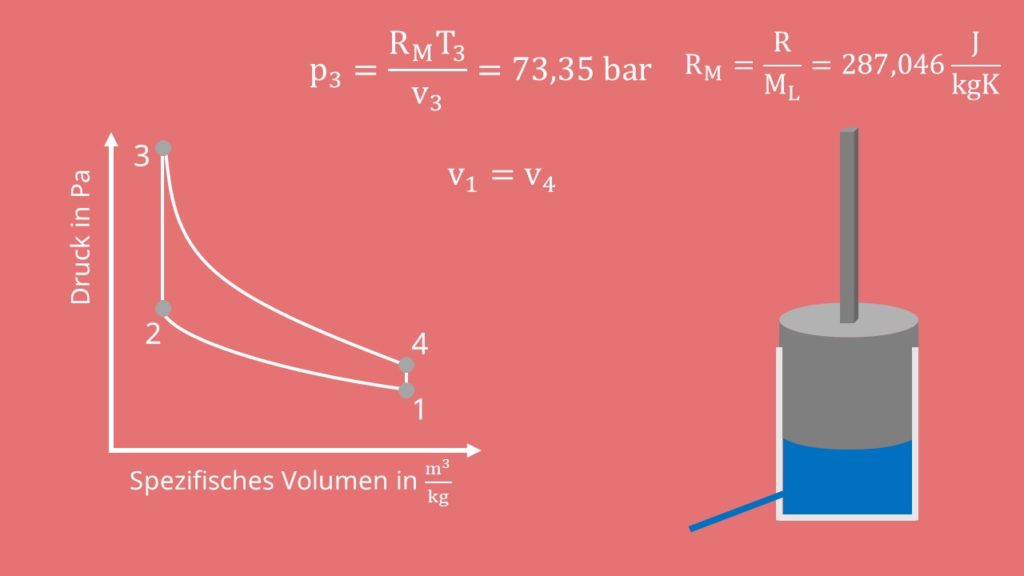
Anschließend folgt eine isentrope Expansion, der Kolben bewegt sich also zurück auf das ursprüngliche Volumen. Wir befinden uns nun im Zustand vier. Hier wissen wir, dass das Volumen 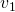 gleich
gleich 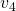 sein muss.
sein muss.
Um auf den ursprünglichen Zustand zu kommen, müssen wir noch isochor Wärme abführen. Das machen wir, indem wir das Gas wechseln. Jetzt sind wir wieder beim Zustand eins angekommen.
Jetzt wollen wir noch die unbekannten Drücke 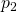 und
und 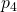 , sowie die unbekannten Temperaturen
, sowie die unbekannten Temperaturen 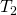 und
und 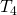 herausfinden.
herausfinden.
Dafür führen wir die sogenannten Isentropen-Beziehungen ein. Allgemein gilt dabei:
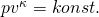
Kappa ist dabei der sogenannte Isentropen Exponent und definiert als 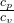 .
.
Es gilt damit also:
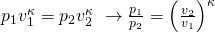
Drücke mit spezifischen Volumina berechnen
Damit können wir uns die fehlenden Drücke berechnen, da wir die spezifischen Volumina alle kennen. Kappa ergibt sich dabei unter Standardbedingungen zu:
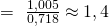
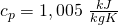
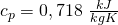
Damit ist:
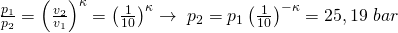
Und:
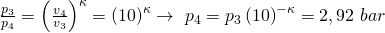
Mit Hilfe des idealen Gasgesetzes erhalten wir auch eine Beziehung für die Temperatur:
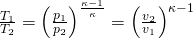
Mit T eins gleich dreihundert Kelvin ergibt sich:
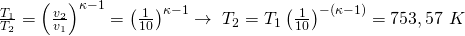
Und mit T drei gleich 2.200 Kelvin:
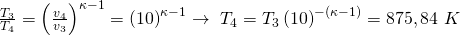
Damit kennen wir nun auch jeden Zustand beim Zweitakt-Kolbenmotor. Für jeden Kreisprozess kannst du so Schritt für Schritt vorgehen und die thermodynamischen Größen bestimmen.
Jetzt weißt du, wie ein Verbrennungsmotor funktioniert und kannst dir jede Position bestimmen.