Ersatzspannungsquelle
In diesem Artikel erklären wir dir, wie Ersatzspannungsquellen dabei helfen, komplexe Widerstandsschaltungen zu vereinfachen. Dabei wird die Schaltung durch eine einzige Quelle und ihrem Innenwiderstand ausgedrückt.
Schau auch direkt in unser Video rein. Darin zeigen wir dir das Vorgehen Schritt für Schritt.
Inhaltsübersicht
Ersatzspannungsquelle und Ersatzstromquelle einfach erklärt
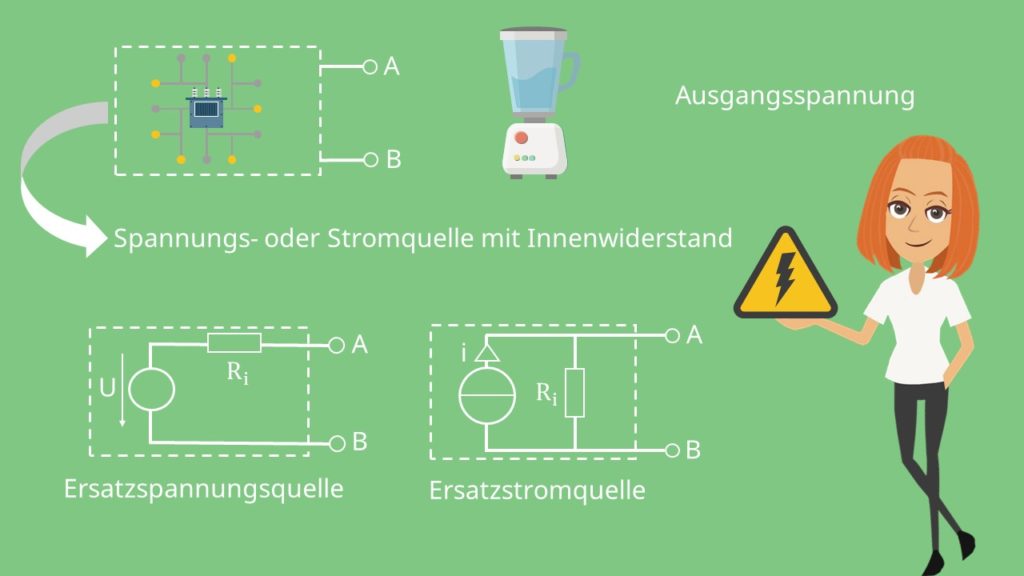
Viele elektrische Geräte sind sehr kompliziert aufgebaut und enthalten viele in Reihe und parallel geschaltete Widerstände oder auch mehrere Strom- und Spannungsquellen. Aber eigentlich interessierst du dich nur für die Ausgangsspannung deines Geräts und willst die Schaltung auf eine Spannungs- oder Stromquelle mit Innenwiderstand reduzieren.
Dafür musst du die Ersatzspannungs- oder Ersatzstromquelle bestimmen. Die Ersatzspannungsquelle, die auch häufig als Thévenin-Theorem bezeichnet wird, hat genau den Wert der Leerlaufspannung zwischen den zwei Ausgangsklemmen A und B. Ihr Innenwiderstand entspricht dem Innenwiderstand zwischen den Anschlussklemmen. Die Ersatzstromquelle nimmt den Wert des Kurzschlussstroms zwischen den besagten Klemmen an. Durch Bestimmen der Ersatzquelle vereinfacht sich deine Schaltung um ein Vielfaches, dadurch ist die anschließende Berechnung einfacher. Im Folgenden zeigen wir dir anhand eines Beispiels genau, wie du vorgehen musst.
Beispielaufgabe: Umzeichnen des Schaltplans
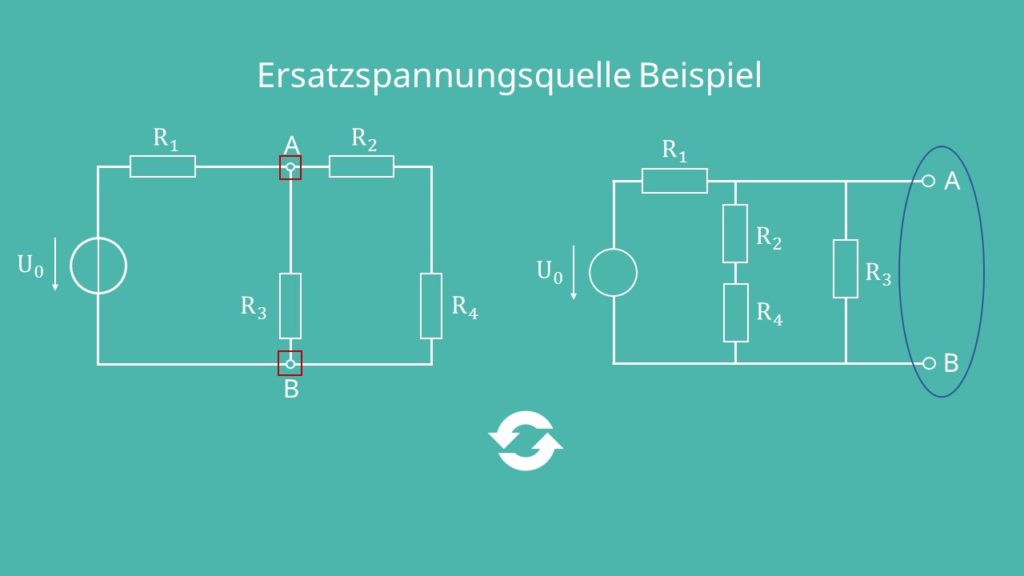
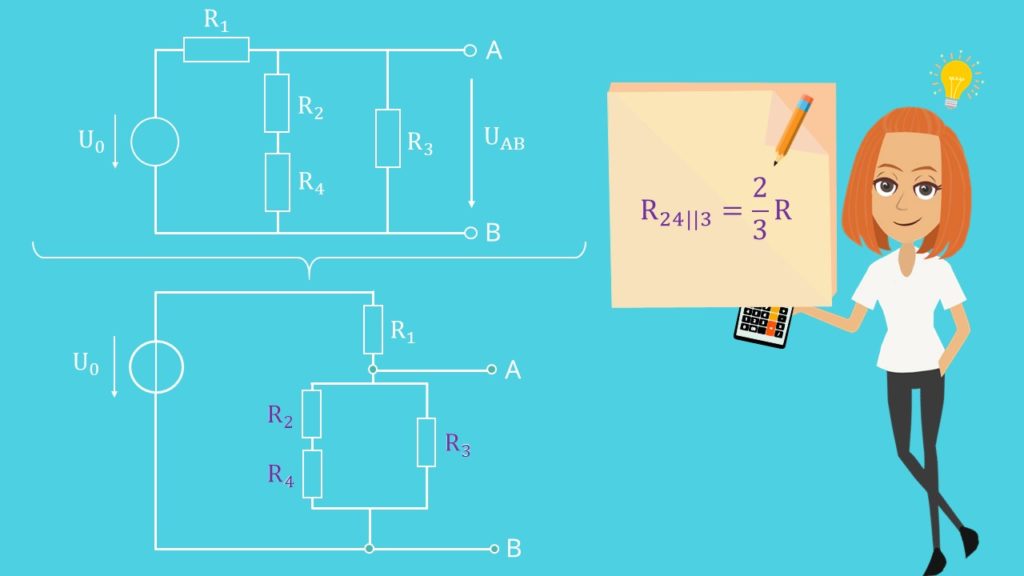
Wir wollen jetzt in folgender Schaltung die Ersatzspannungsquelle und die Ersatzstromquelle zwischen den Klemmen A und B bestimmen.
Die Klemmen sind mitten in der Zeichnung. Das stört die Übersichtlichkeit und daher empfiehlt es sich, die Schaltung etwas umzuzeichnen. Du kannst den Zweig mit Widerstand 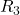 und den mit den Widerständen
und den mit den Widerständen 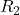 und
und 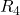 einfach tauschen und schon liegen die Klemmen außen. Aus der Schaltung kannst du sie sogar noch etwas heraus zeichnen.
einfach tauschen und schon liegen die Klemmen außen. Aus der Schaltung kannst du sie sogar noch etwas heraus zeichnen.
Innenwiderstand bestimmen
Um den Innenwiderstand zu bestimmen, schaust du von rechts in die Schaltung zwischen den Klemmen A und B und fasst die Widerstände zu einem Ersatzwiderstand zusammen. Für die Berechnung kannst du alle vorkommenden Spannungsquellen gedanklich kurzschließen. Denn sie haben den Widerstand Null.
Du trennst alle Stromquellen auf. Das entspricht einem unendlich großen Widerstand, sodass kein Strom fließen kann. Unsere Schaltung vereinfacht sich durch Kurzschließen der Spannungsquellen und Auftrennen der Stromquellen zu:
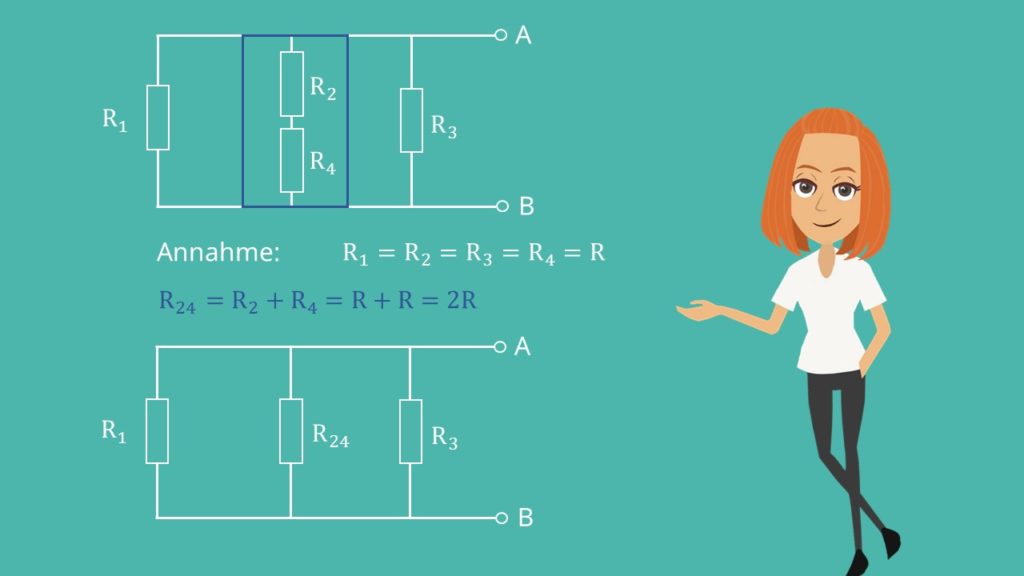
Wie du erkennen kannst, sind jetzt nur noch Widerstände in der Schaltung. Der Innenwiderstand unserer Ersatzquelle entspricht dem Ersatzwiderstand zwischen den Klemmen. Daher können wir nun die Widerstände Schritt für Schritt zusammenfassen. Der Einfachheit halber nehmen wir an, dass alle Widerstände gleich groß sind und den Wert 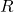 haben.
haben.
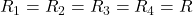
Anschließend bietet es sich an, die Reihenschaltung aus 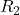 und
und 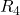 zu
zu 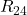 zusammenzufassen.
zusammenzufassen.
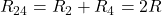
Nun liegt eine Parallelschaltung von 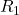 ,
, 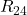 und
und 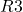 vor.
vor.
Jetzt fassen wir zunächst die Parallelschaltung von 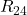 und
und 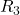 zusammen. Du könntest auch direkt alle drei parallel geschalteten Widerstände zusammenfassen, aber
zusammen. Du könntest auch direkt alle drei parallel geschalteten Widerstände zusammenfassen, aber 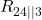 können wir später für die Bestimmung der Leerlaufspannung
noch gebrauchen.
können wir später für die Bestimmung der Leerlaufspannung
noch gebrauchen.
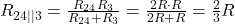
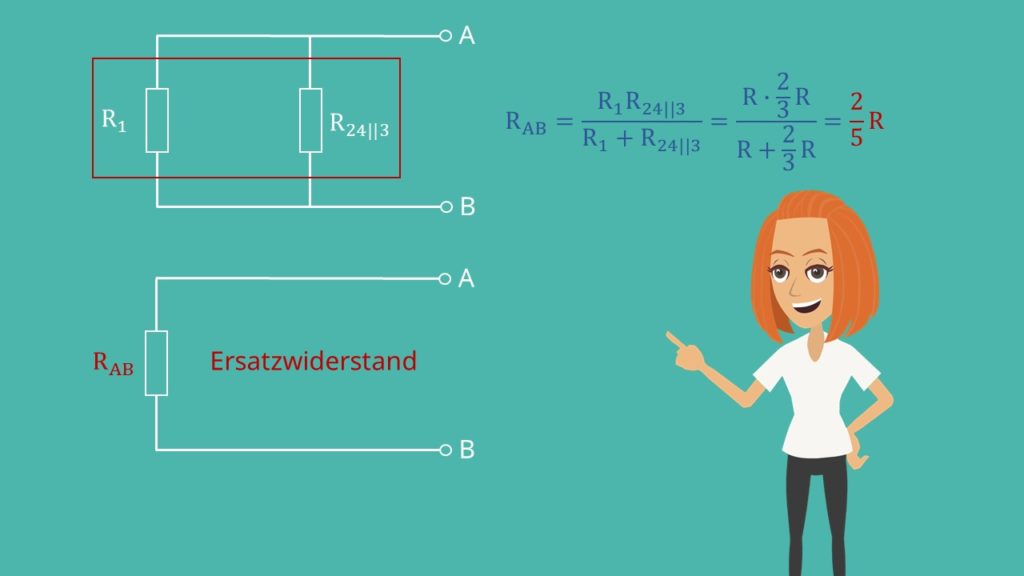
Im nächsten und letzten Schritt fassen wir die parallelen Widerstände 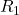 und
und 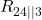 zusammen. Die Rechnung ergibt
zusammen. Die Rechnung ergibt 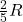 . Das ist der Ersatzwiderstand zwischen den Klemmen A und B.
. Das ist der Ersatzwiderstand zwischen den Klemmen A und B.
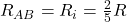
Leerlaufspannung berechnen
Im nächsten Schritt bestimmst du die Klemmenspannung 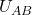 , wenn an den Klemmen keine Last hängt, wird diese als Leerlaufspannung der Schaltung bezeichnet. Sie wird der Spannung
, wenn an den Klemmen keine Last hängt, wird diese als Leerlaufspannung der Schaltung bezeichnet. Sie wird der Spannung 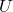 deiner Ersatzquelle entsprechen. Wir schauen uns dafür folgende Schaltung an:
deiner Ersatzquelle entsprechen. Wir schauen uns dafür folgende Schaltung an:
Die Widerstände 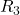 ,
, 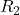 und
und 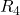 haben wir schon zusammengefasst. Und dieses Ergebnis können wir jetzt verwenden.
haben wir schon zusammengefasst. Und dieses Ergebnis können wir jetzt verwenden.
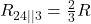
Die gesuchte Klemmenspannung 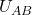 liegt in diesem Fall an der Parallelschaltung aus
liegt in diesem Fall an der Parallelschaltung aus 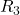 und der Reihenschaltung aus
und der Reihenschaltung aus 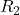 und
und 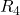 . Wenn dir die Spannung
. Wenn dir die Spannung 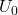 bekannt ist, kannst du
bekannt ist, kannst du 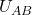 einfach über den Spannungsteiler
bestimmen.
einfach über den Spannungsteiler
bestimmen.
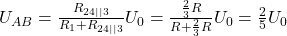
Damit hast du eine komplexe Schaltung auf eine Ersatzspannungsquelle reduziert. Zusammengefasst gilt für diese Schaltung also.
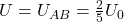
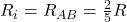
Ersatzstromquelle bestimmen
Alternativ zur Ersatzspannungsquelle kannst du auch die Ersatzstromquelle bestimmen. Wenn du zuvor bereits die Ersatzspannungsquelle bestimmt hast, ist es besonders einfach. Der Strom der Ersatzspannungsquelle ergibt sich aus dem Kurzschlussstrom unserer Schaltung. Der Kurschlussstrom ist der Strom, der über die Klemmen fließt, wenn sie kurzgeschlossen, also ideal verbunden sind. Da wir bereits die Ersatzschaltung bestimmt haben, ergibt sich der Kurschlussstrom 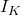 zu:
zu:
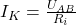
Mit 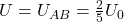 und
und 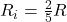 folgt:
folgt:
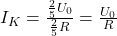
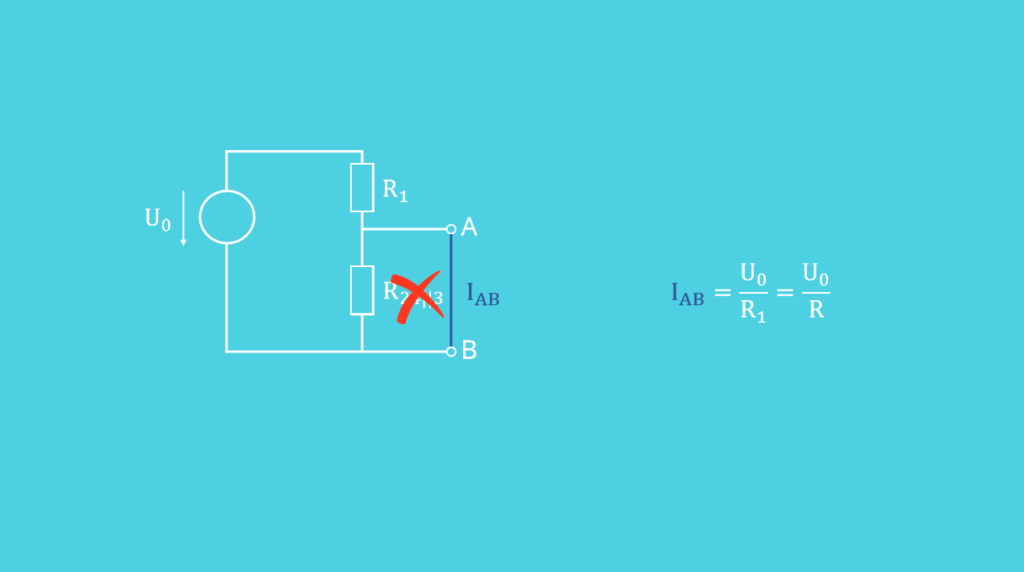
Wenn du zuvor noch nicht die Ersatzspannungsquelle berechnet hast, kannst die die Ersatzstromquelle auch direkt aus der Schaltung bestimmen. Dafür schließt du in der Schaltung die Klemmen A und B kurz.
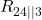 kannst du ignorieren, da der Widerstand kurzgeschlossen wird. Übrig bleibt nur
kannst du ignorieren, da der Widerstand kurzgeschlossen wird. Übrig bleibt nur 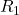 . Der Kurzschlussstrom ist also:
. Der Kurzschlussstrom ist also:
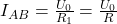
Damit hast du auch die Kennwerte der Ersatzstromquelle bestimmt: 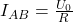 und
und 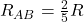 .
.
Weitere Möglichkeit: Anwendung des Ohm’schen Gesetzes
Es gibt noch eine zweite Möglichkeit, den Innenwiderstand einer Schaltung zu bestimmen. Wenn du den Kurzschlussstrom und die Leerlaufspannung zwischen den Klemmen A und B kennst, kannst du mit dem Ohm’schen Gesetz aus ihnen den Ersatzwiderstand berechnen.
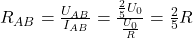
Für unsere Schaltung ergibt sich über diese Rechnung ebenfalls 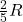 . Wir haben also alles richtig gemacht.
. Wir haben also alles richtig gemacht.