Federkonstante
Für jede lineare Feder kann eine Federkonstante im Zugversuch bestimmt werden. In diesem Beitrag zeigen wir dir die Definition und Herleitung und wie sie bestimmt werden kann.
Aufgepasst: Wenn du das Thema noch besser verstehen willst schau dir einfach unser Video dazu an. Hier erklären wir dir alles nochmal kurz, knapp und verständlich.
Inhaltsübersicht
Definition Federkonstante
Die Federkonstante ist auch als Federhärte, Federrate, Richtgröße, Federsteifigkeit oder Direktionskonstante bekannt. Sie beschreibt das Verhältnis der auf eine Feder wirkenden Kraft und der dadurch bedingten Längenänderung der Feder. Die Federsteifigkeit gilt nur für eine bestimmte Feder und ist damit keine Materialkonstante.
Zugfeder
Die Zugfeder ist eine aus Runddraht schraubenförmig gewundene Feder ohne Windungsabstand und wird deshalb nur bei Zug beansprucht. Die Federsteifigkeit D kann mit der Formel
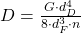
berechnet werden. Hierbei ist G der Schubmodul, dD der Drahtdurchmesser, dF der mittlere Federdurchmesser und n die Anzahl der Windungen.
Druckfeder
Die Druckfeder ist ähnlich aufgebaut wie die Zugfeder, jedoch mit einem Windungsabstand größer null. Somit reagiert die Druckfeder auf Druck und wird in der Technik oft zur Dämpfung eingesetzt, wie zum Beispiel in Automobilen. Die Federkonstante der Druckfeder berechnet sich analog zur Zugfeder.
Schenkelfeder
Die Schenkelfeder, auch Drehfeder genannt, wird bei Drehbewegungen als mechanischer Kraftspeicher verwendet. Sie findet zum Beispiel Verwendung in Schließsystemen oder Autositzen. Die Federkonstante einer Schenkelfeder ist mit dem Drehmoment M und dem Drehwinkel α berechenbar:
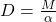
Nichtlineare Federn
An dieser Stelle ist zu erwähnen, dass es auch Federn mit nichtlinearer Steifigkeit gibt, wie zum Beispiel die Luftfeder. Diese werden im Folgenden jedoch nicht näher behandelt.
Federkonstante Formel und Einheit
Die Federkonstante D ist der Quotient aus der auf eine Feder wirkenden Kraft F und der dadurch bedingten Längenänderung ∆L der Feder
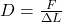
Die Einheiten der Größen sind gegeben durch:
D in 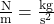
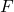 in N,
in N, 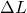 in m.
in m.
Die Federkonstante wird oft auch mit den Buchstaben k oder c verwendet.
Federkonstante Herleitung
Zur Herleitung der Federkonstante geht man zunächst von einer unbelasteten Feder aus. Wird die Feder mit der Masse m belastet, so wirkt auf die Feder die Gewichtskraft 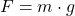 . Die Feder wird dadurch solange um die Strecke s gestreckt, bis die Kraft der Feder FS der Gewichtskraft F entspricht. Bei linearen Federn ist die Kraft F auf die Feder proportional zur Auslenkung, so dass der Quotient der Kraft F dividiert durch die Auslenkung ∆L eine Konstante ist. Diese Konstante wird Federkonstante genannt.
. Die Feder wird dadurch solange um die Strecke s gestreckt, bis die Kraft der Feder FS der Gewichtskraft F entspricht. Bei linearen Federn ist die Kraft F auf die Feder proportional zur Auslenkung, so dass der Quotient der Kraft F dividiert durch die Auslenkung ∆L eine Konstante ist. Diese Konstante wird Federkonstante genannt.
Mit der Formel
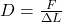
kann man sie berechnen. Diese Formel beschreibt die elastische Verformung von Festkörpern, unter der Annahme, dass deren Verformung proportional zur einwirkenden Kraft ist. Das ist auch als das Hooksche Gesetz bekannt.
Elastizitäts- und Schubmodul
Die Federkonstante hängt von dem verwendeten Material, der Form der Feder, sowie von der Belastungsrichtung ab. Betrachtet man zum Beispiel einen Stab als Feder, so kann sie mit
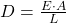
berechnet werden. Hierbei ist E der Elastizitätsmodul, A die Querschnittsfläche und L die Länge des Stabes. Der Elastizitätsmodul ist ein Materialkennwert und beschreibt den proportionalen Zusammenhang zwischen Spannung σ und Dehnung bei der Verformung eines festen Körpers. Er kann mit
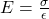
berechnet werden. Hierbei ist die Spannung definiert durch 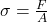 .
.
Mehr zum Elastizitätsmodul und seiner Formel findest du in unserem Beitrag dazu!
Die Dehnung erhält man über den Quotienten der Längenänderung ∆ L und der Ausgangslänge
L, also 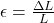 .
.
Die Federsteifigkeit kann auch in Abhängigkeit des Schubmoduls G ausgedrückt werden.
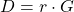
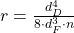
Hierbei hängt die Konstante r von dem Drahtdurchmesser dD, dem mittleren Federdurchmesser dF und der Anzahl der Windungen n ab. Der Schubmodul beschreibt die Verformung eines festen Körpers in Folge von Schubspannung und steht mit dem Elastizitätsmodul in folgender Beziehung
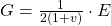 .
.
ν ist hierbei die Poissonzahl, die sich aus der Verformung eins Materials berechnen lässt.
Zugversuch
Ein einfaches Experiment, mit dem die Federsteifigkeit bestimmt werden kann, ist der Zugversuch. Hierbei wird auf ein Material eine bestimmte Zugkraft ausgeübt, was zur Streckung des Materials führt. Über die aufgewendete Kraft F und der Längenänderung des Materials 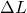 , lässt sich die Federkonstante D berechnen.
, lässt sich die Federkonstante D berechnen.
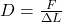
Wenn du noch genauer wissen willst, wie der Zugversuch aussieht und wie er mit der Federkonstante zusammenhängt, dann schau dir gerne unseren Beitrag dazu an!
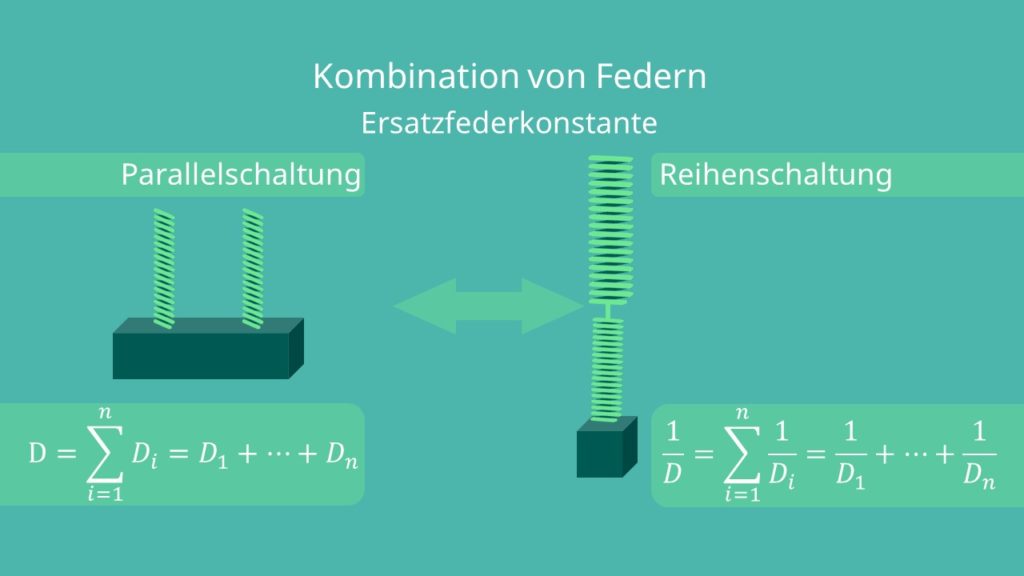
Kombination von Federn
Mehrere Federn können auch beliebig kombiniert werden. Um bei komplexen Systemen die Berechnung zu vereinfachen, berechnet man eine Ersatzfederkonstante, die die Konstanten der einzelnen Federn ersetzt. Hierbei unterscheidet man die Parallelschaltung und die Reihenschaltung von Federn. Bei der Parallelschaltung werden n Federn mit den Federkonstanten D1, …, Dn nebeneinander angeordnet. Dahingegen werden Federn bei einer Reihenschaltung hintereinander angeordnet. Die Ersatzfederkonstante der Parallelschaltung lässt sich dabei über die Summe der einzelnen Federkonstanten berechnen
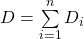
Für die Reihenschaltung erhält man dagegen die Ersatzfederkonstante über die Summe der inversen Federkonstanten.
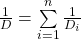
Je nach Komplexität des zu betrachtenden Systems können und müssen diese Formeln kombiniert werden.