Freier Fall
Wie lautet die Formel für den freien Fall und warum ist sie in der Physik so wichtig? Das erfährst du hier und im Video! Außerdem haben wir für dich Videos mit Übungsaufgaben und Klausuraufgaben vorbereitet.
Inhaltsübersicht
Freier Fall einfach erklärt
Unter dem freien Fall verstehst du in der Physik, wenn ein Körper in Richtung des Erdmittelpunkts fällt. Seine Fallbewegung ist dabei geradlinig und gleichmäßig beschleunigt. Auf einen Körper im freien Fall wirken keine Kräfte, bis auf die Gewichtskraft.
Die Gewichtskraft bewirkt eine Beschleunigung, die überall auf der Erde gleich groß ist: 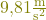 . Sie nennst du auch den Ortsfaktor
oder Fallbeschleunigung. Dadurch fallen alle Körper im freien Fall gleich schnell. Das bedeutet, dass die Masse des Körpers keine Rolle spielt. Das siehst du auch an der Formel des freien Falls, mit der du die Fallzeit t berechnest:
. Sie nennst du auch den Ortsfaktor
oder Fallbeschleunigung. Dadurch fallen alle Körper im freien Fall gleich schnell. Das bedeutet, dass die Masse des Körpers keine Rolle spielt. Das siehst du auch an der Formel des freien Falls, mit der du die Fallzeit t berechnest:
![Rendered by QuickLaTeX.com \[t=\sqrt{\frac{2\cdot\textcolor{magenta}{y_0}}{\textcolor{olive}{\text{Ortsfaktor}}}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-258faa5bcb936d73cb89d95829559002_l3.png)
Denn neben dem Ortsfaktor ist die einzige Größe, die bei der Berechnung wichtig ist, die Fallhöhe y0. In der Realität gilt das nur für eine geringe Fallhöhe. Denn wenn du beispielsweise eine Feder und einen Stein aus 5 Meter Höhe fallen lässt, wird die Feder stärker vom Luftwiderstand abgebremst und kommt nach dem Stein auf.
Bewegungsgesetze freier Fall
Den freien Fall kannst du durch verschiedene Bewegungsgesetzte beschreiben. Mit ihrer Hilfe untersuchst du entweder die Beschleunigung eines Körpers, den Weg des freien Falls oder die Geschwindigkeit, die ein Körper erreicht.
Grafisch kannst du sie in sogenannten Bewegungsdiagrammen darstellen. In den Diagrammen ist wichtig, wie die y-Achse orientiert ist. Sie kann nämlich nach oben oder unten gerichtet sein.
- Ortsachse nach oben orientiert heißt: du lässt das Objekt in einer Höhe bei Punkt y0 los und es triff in Punkt 0 auf den Boden auf.
- Ortsachse nach unten orientiert heißt: du lässt du ein Objekt in einer Höhe bei Punkt 0 los und es trifft in Punkt y0 auf den Boden auf.
Bei den folgenden Bewegungsgesetzen betrachten wir eine nach unten orientierte Ortsachse.
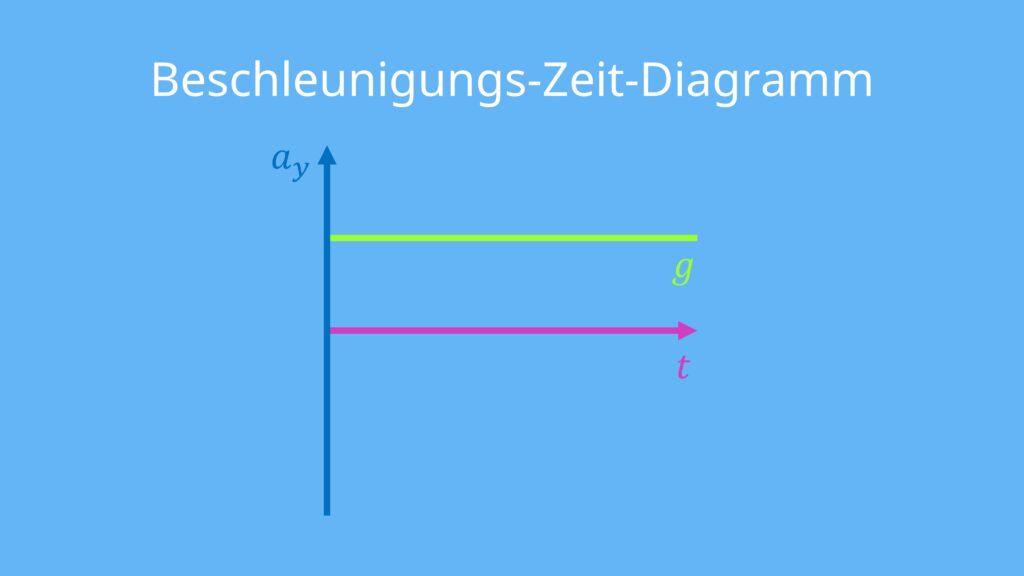
Freier Fall Zeit-Beschleunigung Gesetz
Die erste Beschreibung des freien Falls kannst du mit der Hilfe des Zeit-Beschleunigung Gesetz machen. Wie dir der Name schon sagt, kannst du damit ausdrücken, wie sich die Beschleunigung im Laufe der Zeit, in der der Körper fällt, entwickelt. Die Beschleunigung ist hier gegeben durch die Fallbeschleunigung. Das a-t Diagramm ist beim freien Fall also eine Gerade, weil die Beschleunigung a die Fallbeschleunigung g ist.
Natürlich kannst du das auch in einer Formel angeben:
![Rendered by QuickLaTeX.com \[\textcolor{blue}{a}=\textcolor{olive}{g}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ecf9f45cafe8825a463d18216b1c49cd_l3.png)
Die Beschleunigung a ist gleich der Fallbeschleunigung g.
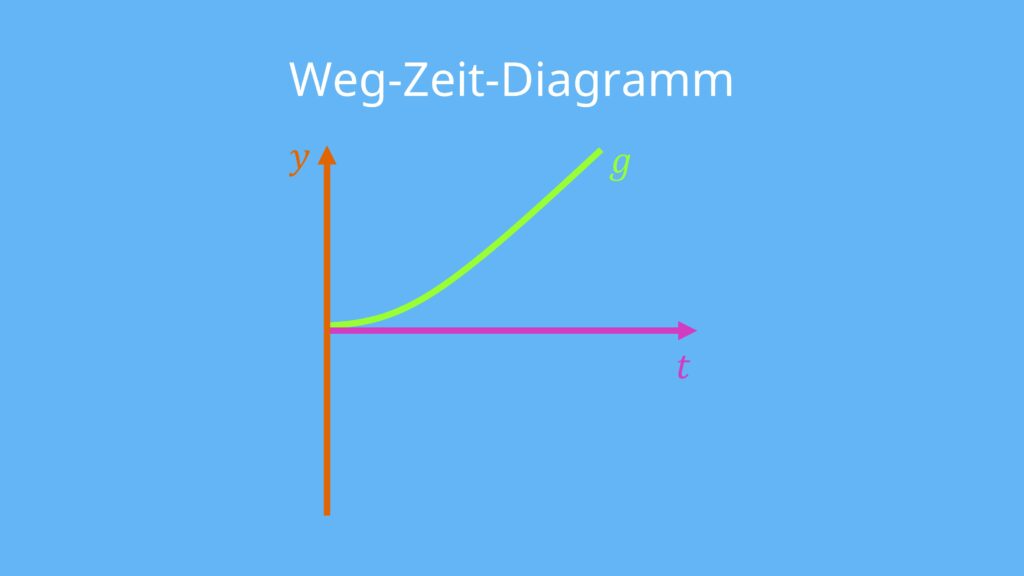
Freier Fall Weg-Zeit Gesetz
Den freien Fall kannst du auch mithilfe des Weg–Zeit Gesetzes (s-t-Gesetz) beschreiben. Du untersuchst also, welche Strecke der Körper in einer bestimmten Zeit fällt.
![Rendered by QuickLaTeX.com \[\textcolor{orange}{y}=\frac{1}{2}\cdot\textcolor{olive}{g}\cdot\textcolor{magenta}{t}^2\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-453b607481ad304379ea2c3de0388702_l3.png)
Dabei wird der Weg y von den Größen Fallbeschleunigung g und der Zeit t des freien Falls bestimmt. Da es sich beim freien Fall um eine gleichmäßig beschleunigte Bewegung handelt, ist der Graph eine Parabel. Das liegt daran, dass der Körper beim Loslassen noch nicht die volle Beschleunigung g hat, sondern kurz braucht, um sie zu erreichen. In dieser Zeit legt der Körper weniger Weg zurück.
In unserem Video zu Geschwindigkeit beschäftigen wir uns genauer mit dem Gesetz. Falls du mehr wissen willst, haben wir dir es hier verlinkt.
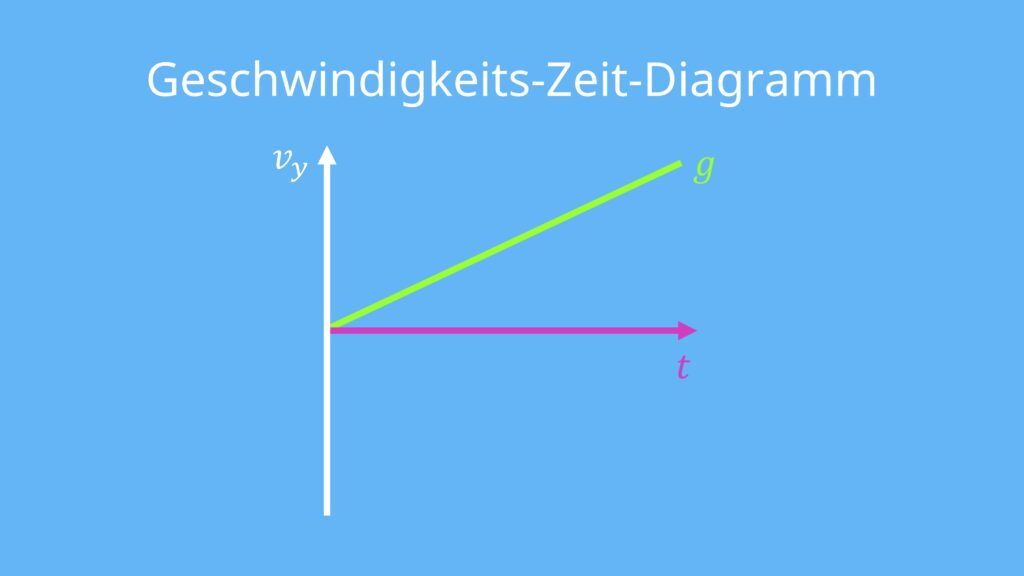
Geschwindigkeit-Zeit Gesetz
Den freien Fall kannst du auch bezüglich seiner Geschwindigkeit beschreiben. Grafisch stellst du das wie folgt dar.
Der freie Fall ist weiterhin eine gleichmäßig beschleunigte Bewegung. Dadurch steigt die Geschwindigkeit mit zunehmender Zeit — die Größen sind also direkt voneinander abhängig. Das erkennst du an der konstant steigenden Gerade.
In einer Formel kannst du das so ausdrücken:
![Rendered by QuickLaTeX.com \[v=\textcolor{olive}{g}\cdot\textcolor{magenta}{t}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-72a5d3faf02b501b5cad3a6ed75a3f64_l3.png)
Auch hier haben also die Fallbeschleunigung g und die Zeit t des freien Falls einen Einfluss auf die Geschwindigkeit v.
Ort-Geschwindigkeit Gesetz
Mit diesem Gesetz verknüpfst du den Ort und die Geschwindigkeit miteinander. Das ist besonders interessant. Denn dadurch kannst du die Geschwindigkeit v ausrechnen, ohne die Fallzeit zu kennen. Mathematisch sieht das so aus:
![Rendered by QuickLaTeX.com \[v=\sqrt{2\cdot\textcolor{olive}{g}\cdot y}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-fcf731e1d926d4c694b876f93475ffc0_l3.png)
Beim Ort-Geschwindigkeit Gesetz hat also noch der zurückgelegte Weg y einen Einfluss.
Freier Fall Formel
Eine wichtige Größe beim freien Fall ist die Fallzeit t. Um sie zu berechnen, benutzt du die Formel:
![Rendered by QuickLaTeX.com \[t=\sqrt{\frac{2\cdot y_0}{g}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-ce55a808b60e3cb8b77b2be5c34a6305_l3.png)
Die Fallzeit t ergibt sich also aus der Wurzel der (zweifachen) Fallhöhe y0, geteilt durch die Fallbeschleunigung g.
Die Berechnung der Fallzeit kannst du dir mit der Hilfe des Weg-Zeit Gesetzes 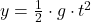 herleiten. Wie du bereits weißt, beginnt der Fall des Körpers am Punkt 0 und endet bei y0. Weil die Höhe zum Endzeitpunkt dann y0 ist, kannst du das Weg-Zeit Gesetz und y0 gleichsetzen:
herleiten. Wie du bereits weißt, beginnt der Fall des Körpers am Punkt 0 und endet bei y0. Weil die Höhe zum Endzeitpunkt dann y0 ist, kannst du das Weg-Zeit Gesetz und y0 gleichsetzen:
![Rendered by QuickLaTeX.com \[y_0=\frac{1}{2}\cdot g \cdot t^{2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1b99e59a7d76a1be148ce9cbac9d291e_l3.png)
Wenn du die Gleichung dann nach t auflöst, ergibt sich:
![Rendered by QuickLaTeX.com \[t^{2}=\frac{2\cdot y_0}{g}\Rightarrow t=\sqrt{\frac{2\cdot y_0}{g}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-09bf7ec644db07645a1587ba6977a8ef_l3.png)
Beachtenswert ist, dass die Fallzeit nicht von der Masse des beobachteten Körpers abhängt. Das liegt an der Vernachlässigung von äußeren Kräften, wie dem Luftwiderstand. Der freie Fall wird also so behandelt, als würde er im Vakuum stattfinden. Hier erreichen Körper mit unterschiedlicher Masse, wenn sie an gleicher Stelle gestartet sind, den Erdboden zur gleichen Zeit.
Expertenwissen: y-Achse nach oben orientiert
In Diagrammen, die den freien Fall grafisch darstellen, musst du aufpassen! Denn manchmal ist die y-Achse nicht nach unten, sondern nach oben orientiert. In diesen Fällen startet der Fall am Punkt y0 und endet beim Punkt 0.
Dadurch ändert sich für dich zum einen, dass das jeweilige Bewegungsdiagramm genau andersherum dargestellt wird. Das berücksichtigst du auch in den Formeln. Beispielsweise wird die Formel 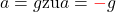 .
.
| Die Formel… | wird zu… |
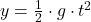 |
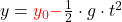 |
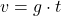 |
 |
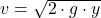 |
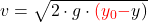 |
Freier Fall Anwendbarkeit
Den freien Fall in der Physik kannst du nicht genau so in die Realität übertragen. Das liegt daran, dass es Einflüsse wie den Luftwiderstand gibt. Er ist nur für bestimmte Gegebenheiten, wie beispielsweise eine geringe Fallhöhe vernachlässigbar. Denn wenn ein Körper für eine längere Zeit fällt, wird er durch den Luftwiderstand abgebremst. Dabei gilt: je schneller der Fall, desto stärker die Abbremsung.
Das bedeutet, die Geschwindigkeit nimmt nicht unendlich zu, sondern erreicht irgendwann ein Maximum. Ein Mensch erreicht beispielsweise eine maximale Geschwindigkeit von ca. 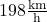 , weil der Luftwiderstand ihn nicht weiter beschleunigen lässt.
, weil der Luftwiderstand ihn nicht weiter beschleunigen lässt.
Freier Fall berechnen
Ein Frachtflugzeug verliert während des Fluges eine Kiste. Sie fällt für 30 Sekunden, wegen der kurzen Dauer kannst du den Fall als freien Fall betrachten. Wie schnell wird die Fracht und welchen Weg legt sie in dieser Zeit zurück?
Zuerst bestimmst du die Geschwindigkeit v der Kiste. Dafür setzt du in die Formel des Geschwindigkeit-Zeit Gesetzes (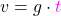 ) ein:
) ein:
![Rendered by QuickLaTeX.com \[v=9,81\frac{\text{m}}{\text{s}²}\cdot\textcolor{magenta}{30\text{s}}=294,3\frac{\text{m}}{\text{s}}\approx1060\frac{\text{km}}{\text{h}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-210abda41d1df3cb6f3cda8d68bf312e_l3.png)
Die Kiste ist nach 30 Sekunden freiem Fall also 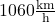 schnell.
schnell.
Wenn du noch berechnen möchtest, welchen Weg die Kiste in der Zeit zurückgelegt hat, kannst du das Weg-Zeit Gesetz (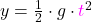 ) anwenden.
) anwenden.
![Rendered by QuickLaTeX.com \[y=\frac{1}{2}\cdot9,81\frac{\text{m}}{\text{s}^2}\cdot(\textcolor{magenta}{30\text{s}})^2=4,4\text{km}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-24160805bbc4fa17d7c10de0f29ce879_l3.png)
Freier Fall Übungsaufgabe
Um dein Wissen zur Berechnung des freien Falls zu vertiefen, schauen wir uns eine Übungsaufgabe an.
Stell dir dazu folgendes Szenario vor:
Du möchtest einen Fallschirmsprung machen und dabei die Schallmauer durchbrechen. Um deinen Fallschirm zu öffnen und dich auf Landegeschwindigkeit abzubremsen, brauchst du 400 Meter. Aus welcher Höhe müsstest du abspringen, wenn du deine Masse und den Luftwiderstand vernachlässigst?
Die Lösung zu dieser Aufgabe mit einem ausführlichen Rechenweg erfährst du in unserem Übungsvideo .
Freier Fall Klausuraufgabe
Zur optimalen Vorbereitung für deine nächste Prüfung schauen wir uns nun eine etwas anspruchsvollere Aufgabe an. Diese kann so oder in ähnlicher Weise auch in deiner Klausur auftauchen.
Stell dir vor, du bist im Urlaub unterwegs und wanderst über eine sehr hohe Brücke. Um herauszufinden, wie hoch sie genau ist, wirfst du einen Stein von der Brücke. Nach 10 Sekunden hörst du den Schall des Aufpralls. Berechne jetzt die Höhe der Brücke, wenn die Schallgeschwindigkeit ungefähr 340 Meter pro Sekunde beträgt. Den Luftwiderstand kannst du dabei vernachlässigen.
In unserem Video zur Klausuraufgabe erklären wir dir Schritt für Schritt, wie du diese Aufgabe bearbeiten kannst.