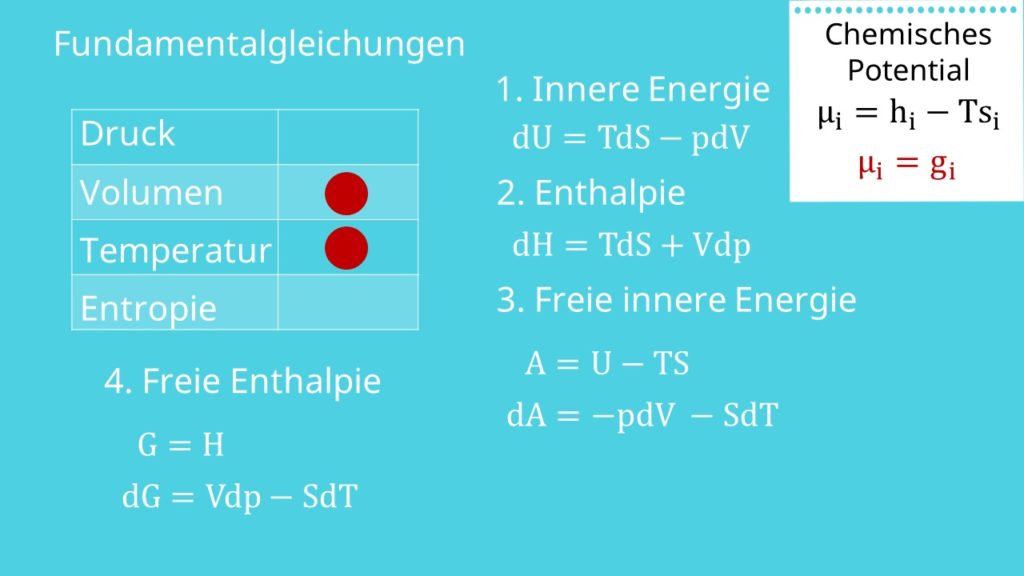
Fundamentalgleichungen der Thermodynamik
Nachdem du im letzten Artikel schon die thermodynamischen Potentiale kennengelernt hast, wollen wir uns jetzt weiteren Fundamentalgleichungen widmen.
Inhaltsübersicht
Einleitung
Darunter versteht man charakteristische Funktionen, die die Gleichgewichtspunkte abbilden. Dabei sind sie nur abhängig von den Größen Druck, Volumen, Temperatur und Entropie. Grundsätzlich werden die Fundamentalgleichungen immer im differentiellen Zustand betrachtet. Wir erhalten damit zwei variable Größen. Da wir den Gleichgewichtszustand erreichen wollen, müssen die Änderungen der Größen beide Null sein. Wenn sie Null sind, dann heißt das für uns, dass die variablen Größen konstant sein müssen.
Innere Energie
Als erstes betrachten wir die innere Energie. Die Fundamentalgleichung kennen wir bereits als:
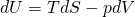
Damit wir im Gleichgewicht sind, muss d U gleich Null sein. Das geht nur, wenn Entropie und Volumen konstant sind.
Die Gleichung für die innere Energie ist jetzt die Grundlage, mit Hilfe der wir die weiteren Gleichungen herleiten. Wir wollen dir die aufwendigen Umformungen allerdings ersparen und zeigen dir nur das Ergebnis und dessen Interpretation.
Enthalpie
Wir beginnen mit der Enthalpie. Als Fundamentalgleichung ergibt sich:
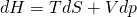
Die Differentiale auf der rechten Seite sind nur d S und d p. Das heißt: Um das Gleichgewicht der Enthalpie zu erhalten, müssen Entropie und Druck konstant bleiben.
Freie innere Energie
Als nächstes führen wir eine neue Größe ein: Die sogenannte freie innere Energie. Sie zeichnet sich dadurch aus, dass wir von der inneren Energie das Produkt von Temperatur und Entropie abziehen. Damit ergibt sich die Definition zu:
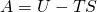
Als Fundamentalgleichung, also in differentieller Form, erhalten wir:
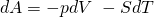
Freie Enthalpie
Hier befinden wir uns im Gleichgewichtszustand, wenn das Volumen und die Temperatur konstant gehalten werden.
Als letztes führen wir die Größe der freien Enthalpie ein. Analog zur inneren Energie ziehen wir hier von der Enthalpie das Produkt von Temperatur und Entropie ab. Damit ergibt sich die Definition zu:
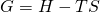
Das kommt dir sicher bekannt vor, vom chemischen Potential. Das heißt also, dass das chemische Potential die molare freie Enthalpie ist.
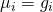
Als Fundamentalgleichung in differentieller Form ergibt sich für die freie Enthalpie:
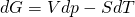
Hier erhalten wir das Gleichgewicht bei konstantem Druck und konstanter Temperatur. Das heißt, wir können das chemische Gleichgewicht mit Hilfe von Druck und Temperatur manipulieren.
Du erkennst vielleicht, dass wir bei der freien inneren Energie beziehungsweise freien Enthalpie einfach T S subtrahieren. Doch warum machen wir das? Dafür denken wir noch mal zurück an die Anergie und Exergie. Aus dem Video dazu weißt du sicher noch, dass bei steigender Entropie der Anteil an Exergie sinkt. Beziehen wir das jetzt wieder auf die freie innere Energie, beziehungsweise die freie Enthalpie, sehen wir, dass wir nur noch den exergetischen, also den für uns nutzbaren Teil, betrachten.
Offene Systeme
Für offene Systeme, beispielsweise Gemische, müssen wir lediglich den bekannten Term für das chemische Potential addieren:
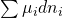
Spezifische Energie
Wir können damit jetzt Formeln in Abhängigkeit jeder Zustandsgröße entwickeln, ohne ein Stoffmodell, wie zum Beispiel das ideale Gas, zu verwenden. Wir machen das jetzt für die spezifische Enthalpie:
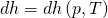
Wir wissen aus der Fundamentalgleichung mit spezifischen Werten:
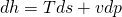
Nun steht noch d s in der Gleichung. Um das zu ändern, stellen wir das totale Differential der Entropie in Abhängigkeit von T und p auf. Es ergibt sich:
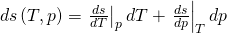
Du erkennst: Wenn wir nach der Temperatur ableiten, halten wir den Druck p konstant und multiplizieren dann nochmal mit d T. Analog machen wir das mit dem Druck.
Setzten wir das ein, erhalten wir eine Gleichung, die unabhängig von s ist:
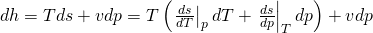
Diese lässt sich noch vereinfachen zu:
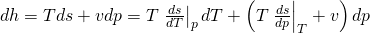
Du siehst, dass in der Gleichung noch Ableitungen stehen. Deshalb bilden wir als nächstes das totale Differential der Enthalpie, wieder in Abhängigkeit von T und p:
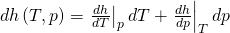
Vergleichen wir jetzt die Koeffizienten vor d p, erkennen wir schnell den Zusammenhang:
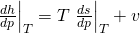
Den Koeffizienten vor d T benötigen wir nicht mehr, er war nur für die Herleitung von d h d p wichtig. Er lässt sich viel einfacher ersetzen mit der Definition von c p:
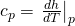
Wir müssen also nur noch d h d p vereinfachen. Die Umformungen wollen wir dir an dieser Stelle ersparen und zeigen dir direkt das Ergebnis:
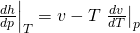
Setzen wir beide Ausdrücke in das totale Differential der Enthalpie ein, erhalten wir unabhängig vom Modell eine Gleichung für d h:
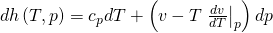
Mit Hilfe der Fundamentalgleichungen kannst du also Formeln für jede Zustandsgröße, wie Druck Enthalpie oder Entropie aufstellen, ohne dass du dafür ein bestimmtes Stoffmodell, wie zum Beispiel das ideale Gasgesetz, verwenden musst.