Gedämpfte Schwingung
In diesem Beitrag zeigen wir dir, was die gedämpfte Schwingung ist, sowie den aperiodischen Grenzfall, Kriechfall und Schwingfall.
Du lernst am einfachsten, wenn du wichtige Inhalte mit Bild und Ton sehen kannst? Dann hilft dir sicher unser Video, um das Thema gedämpfte Schwingung schnell zu verstehen.
Inhaltsübersicht
Gedämpfte Schwingung Definition
Du kannst die gedämpfte Schwingung auch als gedämpfte harmonische Schwingung oder als freie gedämpfte Schwingung bezeichnet. Somit ist sie eine Sonderform der klassischen harmonischen Schwingung . Der schwingende Körper bewegt sich um die sogenannte Ruhelage.
Eine Dämpfung ist eine räumliche oder zeitliche Abnahme der Amplitude dieser jeweiligen Schwingung. Sie entsteht durch eine Umwandlung von Schwingungsenergie in andere Energieformen wie zum Beispiel Wärmeenergie.
Die gedämpfte Schwingung ist durch Reibungsverluste, wie zum Beispiel Luft- oder Gleitreibung charakterisiert. Die durch die Reibung entstehende Dämpfung, wird mit der Dämpfungskonstante und der Abklingkonstante in einer Schwingungsgleichung mathematisch beschrieben. Als Folge der Dämpferkraft verringert sich die Amplitude der Schwingung schrittweise, bis es zu keiner Auslenkung mehr kommt.
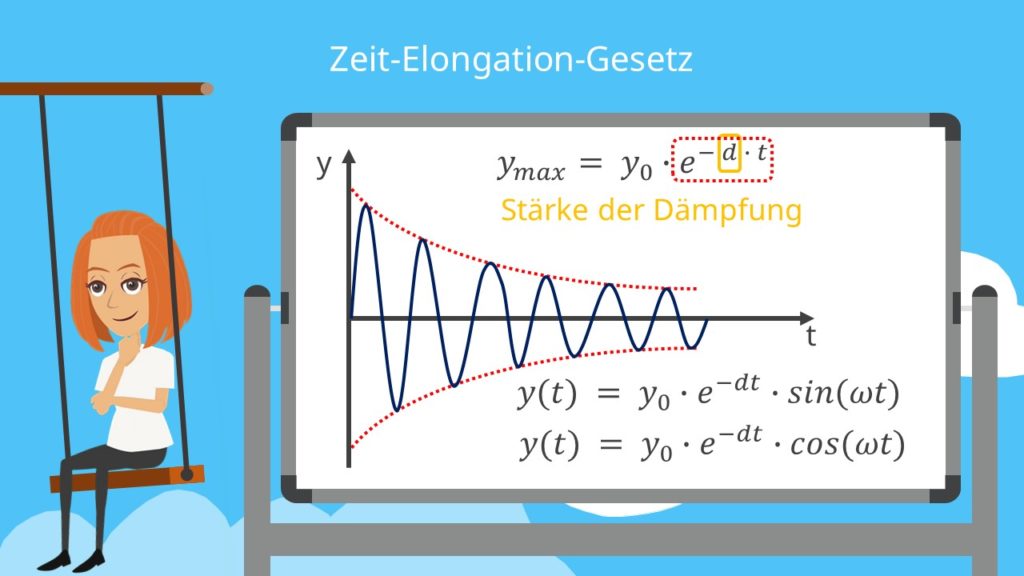
Zeit-Elongation-Gesetz
Die zeitliche Abnahme der Amplitude durch die Dämpfung lässt sich mit einer Exponentialfunktion, dem Zeit-Elongation-Gesetz ausdrücken. Elongation bezeichnet die momentane Auslenkung eines schwingenden Körpers gegenüber der Ruhelage. Mit der Anfangsamplitude 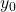 kann die Maximalauslenkung zu jedem beliebigen Zeitpunkt t dargestellt werden. Die Formel lautet dann:
kann die Maximalauslenkung zu jedem beliebigen Zeitpunkt t dargestellt werden. Die Formel lautet dann:
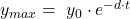
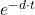 gibt hierbei die Abnahme der Amplitude in Abhängigkeit von der Zeit an. Die Dämpfungskonstante mit Formelzeichen d, manchmal auch k, gibt die Stärke der Dämpfung an.
gibt hierbei die Abnahme der Amplitude in Abhängigkeit von der Zeit an. Die Dämpfungskonstante mit Formelzeichen d, manchmal auch k, gibt die Stärke der Dämpfung an.
Wenn nun die Auslenkung einer gedämpften Schwingung beschrieben werden soll, muss der Ausdruck für y_{max} in die Schwingungsgleichung für harmonische Schwingungen eingesetzt werden. Die Herleitung der Schwingungsgleichung für ein Fadenpendel wurde im Artikel harmonische Schwingungen schon ausführlich behandelt. Bei dem gedämpften Fadenpendel wird einfach noch ein Ausdruck mit der Dämpfungskonstante hinzugefügt.
Man erhält für die Auslenkung einer gedämpften Schwingung:
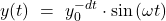 bzw.
bzw. 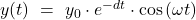
Dämpfungsmaß
Der Verlauf des schwingenden Systems nach einer Anregung kann mit dem dimensionslosen Dämpfungsmaß D, auch Dämpfungsgrad oder Lehrsches Dämpfungsmaß genannt, beschrieben werden. Es gilt:
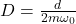
Mit der Masse m, der Dämpfungskonstante d und der Eigenkreisfrequenz des ungedämpften Systems 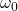 .
.
Bewegungsgleichung
Um die gedämpfte Schwingung zu beschreiben, wird eine mathematische Bewegungsgleichung oder auch Schwingungsgleichung verwendet. Diese bildet die räumliche und zeitliche Entwicklung des mechanischen Systems ab. Die Bewegungsgleichung für das Federpendel wird im Artikel Schwingungsgleichung Federpendel genauer beschrieben.
Bewegungsgleichung gedämpfte Schwingung
Die Bewegungsgleichung für die gedämpfte Schwingung ist relativ ähnlich zur allgemeinen Schwingungsgleichung. Sie soll hier anhand eines Federpendels dargestellt werden. Für die Beschreibung ist die Wahl eines geeigneten Koordinatensystems notwendig. Da sich das Federpendel eindimensional bewegt, genügt eine vektorielle Größe x. Die Bewegungsgleichung eines Pendels mit einer zur Geschwindigkeit proportionalen Dämpfung ist:
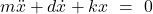
Hier handelt es sich um eine homogene lineare Differentialgleichung 2. Ordnung mit der Masse m und der Federkonstante k . Diese gibt das Verhältnis der auf eine Feder wirkenden Kraft zur dadurch entstehenden Auslenkung der Feder an und wird manchmal auch mit D bezeichnet. Im Artikel Federkonstante wird näher auf diese eingegangen. Durch Lösung dieser Differentialgleichung lässt sich eine Fallunterscheidung nach der Stärke der Dämpfung aufstellen.
Fallunterscheidung Dämpfungskonstante
Die ungedämpfte Eigenfrequenz 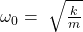 ist bereits aus unserem Artikel Schwingungsgleichung Federpendel bekannt. Die Abklingkonstante
ist bereits aus unserem Artikel Schwingungsgleichung Federpendel bekannt. Die Abklingkonstante 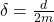 steht bei positivem Vorzeichen für eine abklingende Schwingung und bei negativem Vorzeichen für eine exponentiell zunehmende Schwingung. Diese beiden Konstanten gelten als Voraussetzung für die folgende Fallunterscheidung.
steht bei positivem Vorzeichen für eine abklingende Schwingung und bei negativem Vorzeichen für eine exponentiell zunehmende Schwingung. Diese beiden Konstanten gelten als Voraussetzung für die folgende Fallunterscheidung.
Durch Einsetzen dieser Konstanten erhalten wir die Differentialgleichung in ihrer allgemeinen Form:
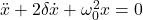
Zur Lösung einer linearen homogenen Differentialgleichung wird der Ansatz 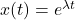 verwendet.
verwendet.
Es ergibt sich:
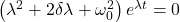
Da 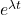 nicht null werden kann, betrachten wir nur den Ausdruck in der Klammer. Dessen Nullstelle kann durch Anwendung der Mitternachtsformel bestimmt werden:
nicht null werden kann, betrachten wir nur den Ausdruck in der Klammer. Dessen Nullstelle kann durch Anwendung der Mitternachtsformel bestimmt werden:
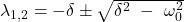
Diese Lösung der Differentialgleichung kann als Linearkombination für beide Parameter dargestellt werden.
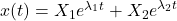
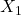 und
und 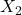 sind die Freiheitsgrade der Funktion. Die Diskriminante
sind die Freiheitsgrade der Funktion. Die Diskriminante 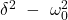 kann unterschiedliche Ausprägungen annehmen. Je nachdem, wie groß die Dämpfungskonstante und damit die Abklingkonstante ist kommt es zu der Fallunterscheidung.
kann unterschiedliche Ausprägungen annehmen. Je nachdem, wie groß die Dämpfungskonstante und damit die Abklingkonstante ist kommt es zu der Fallunterscheidung.
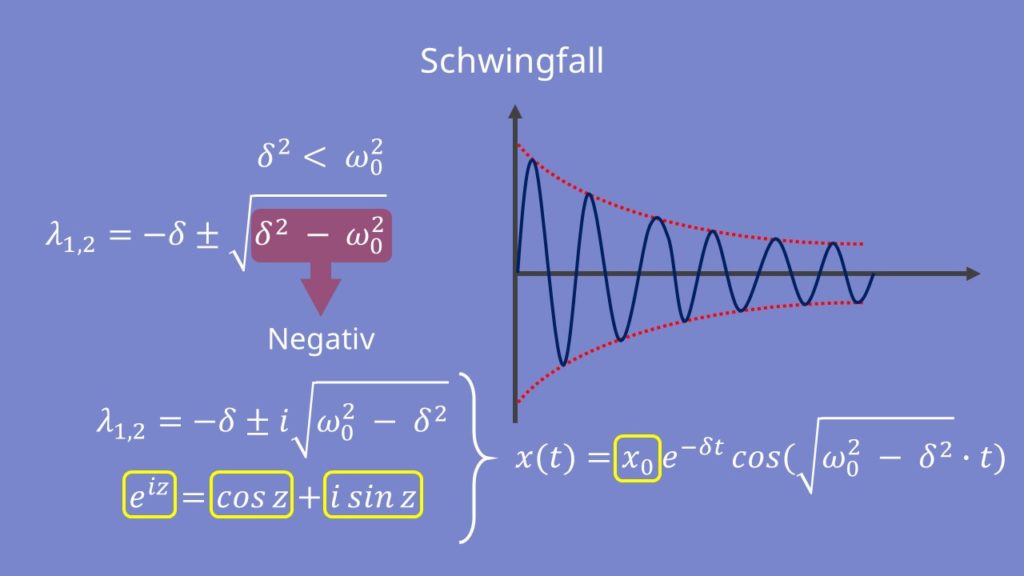
Schwingfall
Wenn die Dämpfungskonstante und die Abklingkonstante kleiner als die Eigenfrequenz 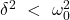 des Systems ist, wird die Diskriminante
des Systems ist, wird die Diskriminante 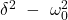 negativ. So wird auch die Wurzel negativ und man erhält zwei konjugiert komplexe Lösungen
negativ. So wird auch die Wurzel negativ und man erhält zwei konjugiert komplexe Lösungen 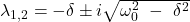 .
.
Wir erhalten als Linearkombination:
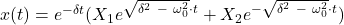
Die Konstanten 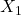 und
und 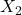 sind die Freiheitsgrade der vorhandenen Lösung, auf deren Berechnung im Artikel Schwingungsgleichung Federpendel eingegangen wird.
sind die Freiheitsgrade der vorhandenen Lösung, auf deren Berechnung im Artikel Schwingungsgleichung Federpendel eingegangen wird.
Mit der eulerschen Formel 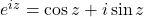 ergibt sich:
ergibt sich:
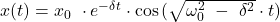
mit der Anfangsamplitude 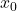 . Dieser Fall wird als Schwingfall bezeichnet.
. Dieser Fall wird als Schwingfall bezeichnet.
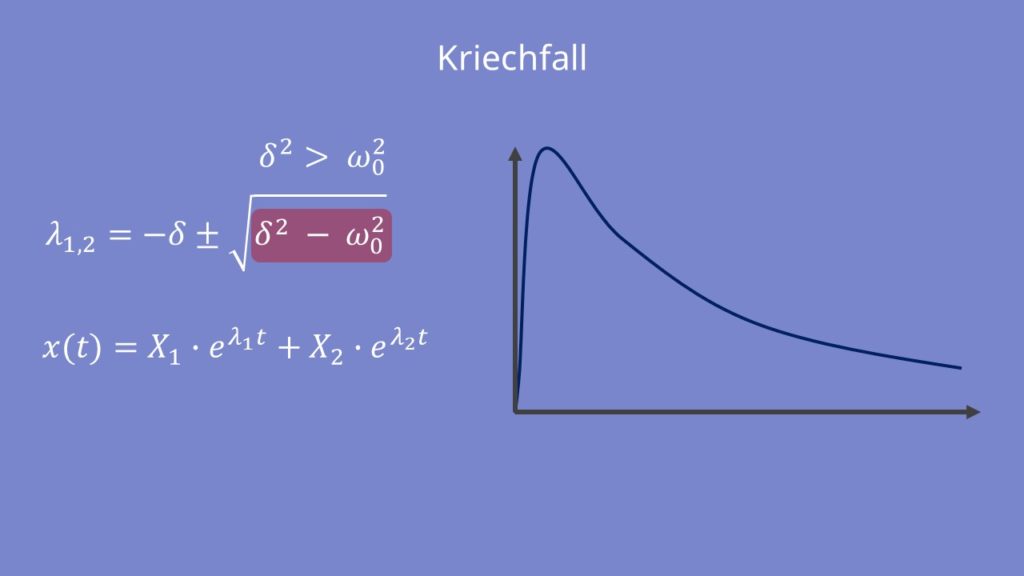
Aperiodischer Grenzfall
Der aperiodische Grenzfall gibt den Punkt im schwingenden System an, an dem keine Schwingung mehr möglich ist. Die Dämpfungskonstante und daher die Abklingkonstante sind gleich der Eigenkreisfrequenz 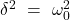 und somit ist
und somit ist 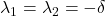 . Der Oszillator kehrt in einer sehr schnellen Zeit zu seiner Ruhelage zurück. Der aperiodische Grenzfall wird auch als kritische Dämpfung bezeichnet.
. Der Oszillator kehrt in einer sehr schnellen Zeit zu seiner Ruhelage zurück. Der aperiodische Grenzfall wird auch als kritische Dämpfung bezeichnet.
Als Ansatz zur Lösung dieser doppelten Nullstelle muss eine zweite Lösung unabhängig kreiert werden:
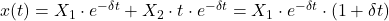
Harmonische Schwingung
Du hast bereits die gedämpfte Schwingung als eine Sonderform der harmonischen Schwingung kennengelernt. Du kannst harmonische Schwingungen grundsätzlich durch eine sinusförmige Funktion beschreiben.
Du willst wissen, wie die harmonische Schwingung aussieht und welche weiteren Arten neben der gefämpften Schwingung zu ihr gehören? Dann schau dir gerne unseren Beitrag dazu an!


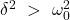 . Die Schwingungsamplitude nach der Zeit x(t) für den Kriechfall setzt sich aus zwei reellen Lösungen zusammen:
. Die Schwingungsamplitude nach der Zeit x(t) für den Kriechfall setzt sich aus zwei reellen Lösungen zusammen: