Hydrostatik – Druck in ruhender Flüssigkeit
Wenn du eine Bierflasche im Wasser kühlst, wirkt auf diese ein bestimmter Druck. Wie du ihn ermitteln kannst, erklären wir dir in den nächsten acht Minuten.
Inhaltsübersicht
Druckberechnung im ruhenden Zustand
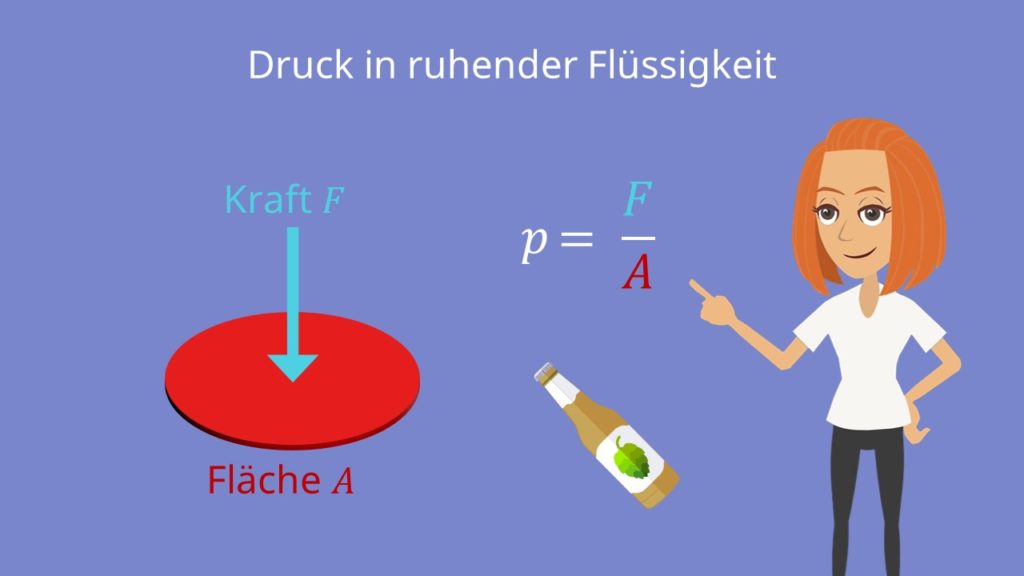
Um den Druck in ruhender Flüssigkeit zu verstehen, musst du erst einmal wissen was Druck überhaupt ist. In diesem Beitrag erklären wir dir alles wichtige zum Druck in ruhender Flüssigkeit.Wird mit einer bestimmten Kraft auf eine Fläche gedrückt, entsteht auf dieser ein gewisser Druck p. Mit der Formel
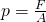
kannst du ihn dann genau berechnen.
Luftdruck und Umgebungsdruck
Du hast bestimmt schon etwas von Luftdruck gehört. Das bedeutet, dass die Luft mit einer gewissen Kraft auf eine Fläche wirkt und Druck entsteht. Jetzt wirst du dich bestimmt fragen, ob auch die Luft, die uns ständig umgibt, einen Druck auf uns und andere Gegenstände ausübt. Die Antwort ist ja. Dieser Druck ist der sogenannte Umgebungs- oder Atmosphärendruck 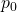 , der immer 1 bar beträgt. In Flüssigkeiten ist es genau dasselbe. Die Flüssigkeit wirkt mit einer bestimmten Kraft auf eine Fläche und übt damit Druck aus. Die Fläche kann entweder die Wände des Behälters sein, in der sich die Flüssigkeit befindet oder auch ein Köper, der in der Flüssigkeit liegt.
, der immer 1 bar beträgt. In Flüssigkeiten ist es genau dasselbe. Die Flüssigkeit wirkt mit einer bestimmten Kraft auf eine Fläche und übt damit Druck aus. Die Fläche kann entweder die Wände des Behälters sein, in der sich die Flüssigkeit befindet oder auch ein Köper, der in der Flüssigkeit liegt.
Jedoch ist es hier nicht so einfach, den Druck zu berechnen. Es müssen noch weitere Einflussfaktoren berücksichtigt werden. Damit du das verstehst, erklären wir es dir am besten anhand eines Beispiels.
Beispiel
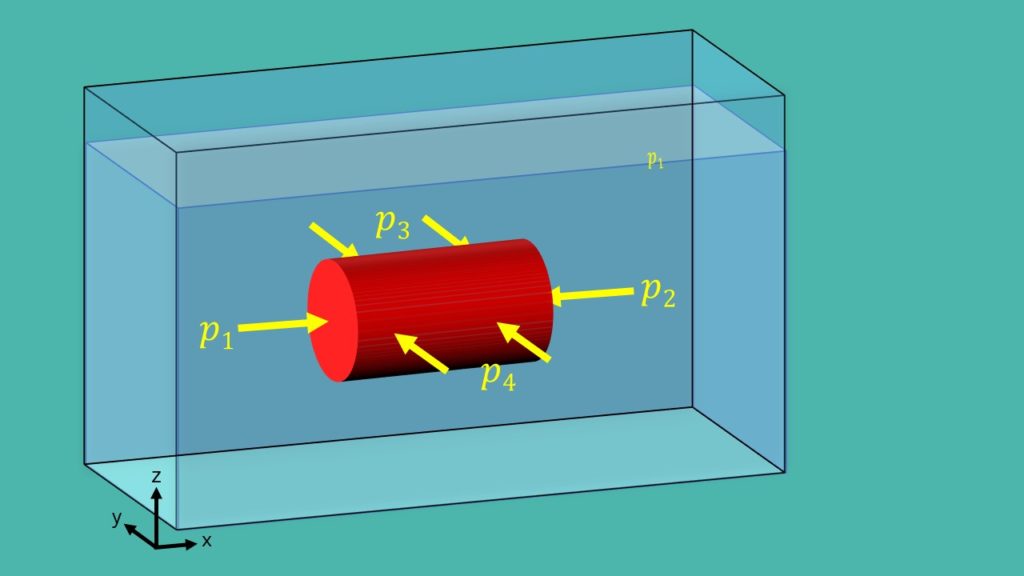
Stell dir vor du hast einen Behälter, der mit einer Flüssigkeit gefüllt ist und nicht bewegt wird. Nun legst du einen Stab in Form eines Zylinders horizontal hinein. Zuerst betrachten wir nur den Druck in x- und y-Richtung.
Wie du siehst wirkt in x- und y-Richtung ein Druck auf den Stab. Die Frage ist jetzt: Wann ist der Zylinder im Gleichgewicht, also wann bewegt er sich weder nach links oder rechts noch nach vorne oder hinten?
Aus der Skizze kann man schließen, dass dafür p1=p2 und p3=p4 sein muss. Da hier kein x oder y vorkommt, hängt der Druck also nicht von x und y ab.
Um nun den Druck in z-Richtung betrachten zu können, verändern wir die Skizze ein klein wenig. Dazu wird der Stab senkrecht statt horizontal in den Behälter gestellt. Da wir ja nun den Druck entlang der z-Achse betrachten, spielt hier auch die Gewichtskraft des Stabes eine Rolle.
Jetzt wirkt der Druck oben und unten auf die Stirnfläche des Zylinders. Um zu wissen wann der Stab im Gleichgewicht ist, ermitteln wir nun das Kräftegleichgewicht.
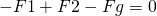
Jetzt stellen wir die Formel 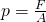 nach F um und setzen diese für F1 und F2 ein. Die Gewichtskraft Fg ist die Masse m mal die Erdbeschleunigung, also
nach F um und setzen diese für F1 und F2 ein. Die Gewichtskraft Fg ist die Masse m mal die Erdbeschleunigung, also 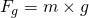 .
.
Die Formel lautet nun 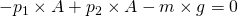
Aus der Physik weißt du, dass die Masse gleich Dichte mal Volumen, also 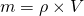 ist. V wiederrum berechnet sich durch Fläche mal Höhe, also
ist. V wiederrum berechnet sich durch Fläche mal Höhe, also 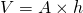 Da gemäß unserer Skizze
Da gemäß unserer Skizze 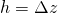 gilt, kannst du nun für die Masse
gilt, kannst du nun für die Masse 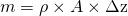 schreiben. Setzt du die Masse in die vorherige Gleichgewichtsbedingung ein, erhältst du
schreiben. Setzt du die Masse in die vorherige Gleichgewichtsbedingung ein, erhältst du 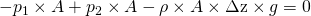 . Wenn du jetzt durch A teilst und nach
. Wenn du jetzt durch A teilst und nach 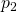 auflöst, siehst du, dass hier nicht nur der Druck
auflöst, siehst du, dass hier nicht nur der Druck 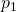 vorkommt, sondern auch die Höhe h. Die Formel lautet also
vorkommt, sondern auch die Höhe h. Die Formel lautet also
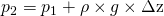 .
.
Allgemeine Formel zur Druckberechnung
Da diese Formel nur genau auf unser Beispiel bezogen ist, erklären wir dir noch den allgemeinen Fall.
Der Druck 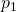 ist der Umgebungsdruck
ist der Umgebungsdruck 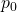 und
und 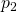 der gesuchte Tiefendruck p. Allgemein lautet die Formel zur Druckberechnung also
der gesuchte Tiefendruck p. Allgemein lautet die Formel zur Druckberechnung also
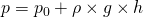 .
.
Fassen wir das nochmal zusammen: Der Druck in einer ruhenden Flüssigkeit ändert sich in x- und y-Richtung nicht. Aber er wächst linear mit zunehmender Wassertiefe h an.
Auch wenn der Druck nicht von x und y abhängt, kann die Flüssigkeit auf Wände trotzdem einen Druck ausüben. Das klingt verwirrend? Keine Angst, das ist alles halb so schlimm. Wir werden es dir wieder anhand eines Beispiels erklären.
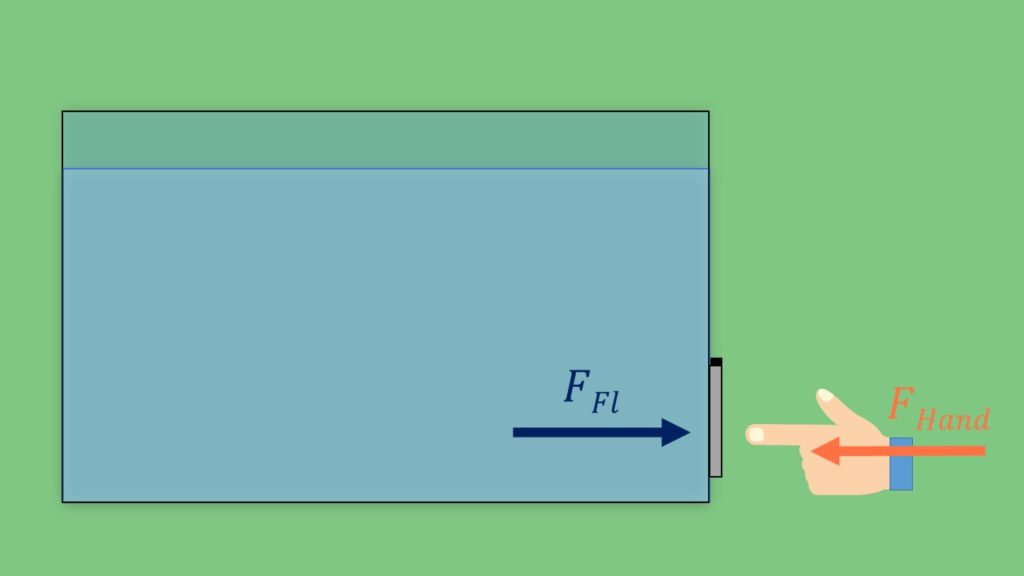
Du hast einen Behälter, der mit einer Flüssigkeit gefüllt ist. Nun hat dieser jedoch auf einer Seite eine kleine rechteckige Klappe, durch die die Flüssigkeit hinaus fließen kann. Da du aber nicht willst, dass dort etwas hinausdringt, drückst du mit deinem Finger dagegen. Du möchtest nun wissen, mit welcher Kraft du dagegen halten musst? Dazu solltest du erst einmal herausfinden, welche Kraft das Fluid von innen auf die Klappe ausübt.
Also wie groß ist die Kraft auf die Fläche A? Von innen wirkt der Flüssigkeitsdruck 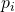 . Wie du gerade gelernt hast, lässt sich dieser mit der Formel
. Wie du gerade gelernt hast, lässt sich dieser mit der Formel
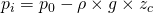 berechnen.
berechnen.
Jetzt stellt sich dir bestimmt die Frage wieso hier 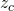 steht.
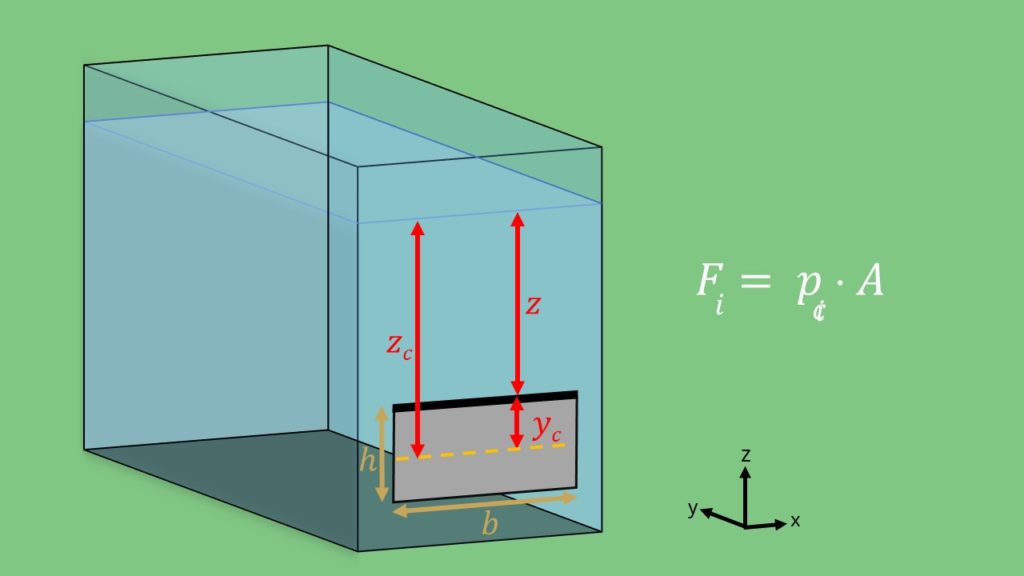
steht. 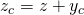 . Mit Hilfe der Skizze kannst du sehen, dass z der Abstand von der Oberfläche bis zum Scharnier der Klappe ist.
. Mit Hilfe der Skizze kannst du sehen, dass z der Abstand von der Oberfläche bis zum Scharnier der Klappe ist. 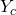 ist nichts Anderes als die Lage des Flächen-Schwerpunktes der Klappe. Bei einem Rechteck also
ist nichts Anderes als die Lage des Flächen-Schwerpunktes der Klappe. Bei einem Rechteck also 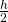 . Aber Achtung: bei der Formel
. Aber Achtung: bei der Formel 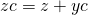 musst du unbedingt darauf achten, wo das Koordinatensystem liegt und die Vorzeichen dementsprechend anpassen!
musst du unbedingt darauf achten, wo das Koordinatensystem liegt und die Vorzeichen dementsprechend anpassen!
Was du ebenfalls bereits weißt ist, dass 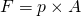 ist. Also ist
ist. Also ist 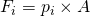 . Da
. Da 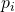 von
von 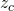 abhängt, schreibt man auch
abhängt, schreibt man auch 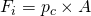 .
.
Weil ja außen nicht nur deine Fingerkraft sondern auch noch der Umgebungsdruck wirkt, muss dieser auch noch berücksichtigt werden. Mit 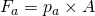 und
und 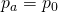 kann man dann die Gesamtkraft berechnen, die auf die Klappe ausgeübt wird:
kann man dann die Gesamtkraft berechnen, die auf die Klappe ausgeübt wird:
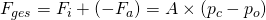 .
.
Setzt du nun für 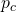
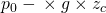 ein, dann erhältst du folgende Gleichung:
ein, dann erhältst du folgende Gleichung:
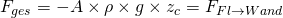 .
.
Da die Kraft ohnehin als Betrag gesehen wird und in Richtung des zugehörigen Vektors gilt, kann das Minus weggelassen werden. Wie du siehst verbleibt offenbar nur der von der Flüssigkeit allein erzeugte Kraftanteil. Der Umgebungsdruck fällt vollkommen weg und ist somit unwichtig.
Das heißt für dich, dass die Kraft, die du aufbringen musst, genauso groß sein muss wie die Kraft, die das Fluid auf die Wand bzw. auf die Klappe ausübt.
Das Ganze kannst du noch optimieren, indem du mit deinem Finger genau dort drauf drückst, wo die Kraft vom Fluid an der Klappe angreift. Aber wo ist das? Kann man das berechnen? Ja das kannst du. Sogar relativ schnell.
Dazu stellen wir ein Momentengleichgewicht um das Scharnier der Klappe auf. Das heißt wir betrachten die Kräfte mit ihrem Angriffspunkt, die bewirken, dass sich die Klappe um das Scharnier bewegt. Wie wir bereits festgestellt haben, drückt von innen die Kraft des Fluides und von außen der Umgebungsdruck. Der Abstand vom Scharnier zum Kraftangriffspunkt ist dabei der sogenannte Hebel, den wir mit y bezeichnen. Die Gleichung lautet also:
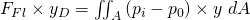 .
.
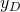 ist hierbei die Lage des Kraftangriffspunktes, die nicht automatisch der des Flächenschwerpunktes entspricht.
ist hierbei die Lage des Kraftangriffspunktes, die nicht automatisch der des Flächenschwerpunktes entspricht.
Da 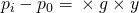 ist, erhältst du durch Einsetzen
ist, erhältst du durch Einsetzen
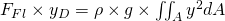 .
.
Das Doppelintegral 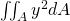 wird als Trägheitsmoment eines Körpers um die x-Achse beschrieben. Dieses wird mit
wird als Trägheitsmoment eines Körpers um die x-Achse beschrieben. Dieses wird mit 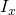 bezeichnet. Schreiben wir nun statt dem Integral
bezeichnet. Schreiben wir nun statt dem Integral 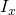 und lösen nach
und lösen nach 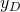 auf, so erhalten wir
auf, so erhalten wir
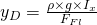 .
.
Wie du bereits weißt ist {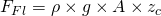 . Da wir aber nur den Abstand vom Scharnier zum Flächenschwerpunkt benötigen, wird
. Da wir aber nur den Abstand vom Scharnier zum Flächenschwerpunkt benötigen, wird 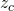 zu
zu 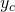 . Du erhältst also:
. Du erhältst also:
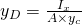 .
.
Mit dem Satz von Steiner sind wir dann auch fast schon am Ziel. Dieser Satz lautet: {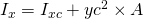 . Wenn wir ihn in unsere {
. Wenn wir ihn in unsere {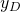 – Gleichung einsetzen, hast du endlich die fertige Formel. Diese lautet dann also
– Gleichung einsetzen, hast du endlich die fertige Formel. Diese lautet dann also
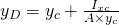 .
.
Mit 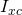 ist das Flächenträgheitsmoment bezüglich des Flächenschwerpunktes gemeint und beträgt bei einem Rechteck
ist das Flächenträgheitsmoment bezüglich des Flächenschwerpunktes gemeint und beträgt bei einem Rechteck 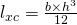
Für andere Flächen kannst du diese Formel in der Formelsammlung nachschlagen.
So, nun bist du bestens informiert über den Druck in einer Flüssigkeit und wie sie sich auf verschiedene Konstruktionen auswirkt. Mach’s gut und bis bald.