Isochore Zustandsänderung
In diesem Beitrag betrachten wir isochore Zustandsänderungen. Du erfährst, wie sich der Verlauf im p-V- sowie im T-s-Diagramm darstellt und wie sich die thermischen Zustandsgrößen verhalten.
Die isochore Zustandsänderung gehört zusammen mit der isobaren und isothermen , zu jenen Zustandsänderungen, bei denen eine thermische Zustandsgröße konstant bleibt. Im isochoren Fall ist dies das Volumen. Der Begriff „isochor“ kommt aus dem Griechischen und bedeutet „gleicher Raum“.
Inhaltsübersicht
Thermische Zustandsgleichung
Im Gegensatz zum Volumen ändern sich während des Prozesses die Temperatur und der Druck. Der Grund dafür ist der Wärmetransport. Wird einem Gas, bei konstantem Volumen, Wärme zugeführt, dann erhöht sich die Temperatur und die innere Energie, welche wiederum den Druck im System steigen lässt.
Aber ganz langsam von Anfang an. Betrachten wir zunächst die thermische Zustandsgleichung, welche allgemein mit
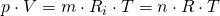
gegeben ist und erinnern uns dabei an die isochore Einschränkung eines konstanten Volumens
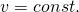 oder
oder 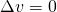 ,
,
dann erhalten wir für die Zustandsgleichung folgende Beziehung zwischen Druck p und Temperatur T:
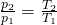
Diese Formel ermöglicht es uns, Zustandsgrößen des ersten Zustands oder des zweiten Zustands zu berechnen, indem wir diese einfach nach der gesuchten Größe umformen.
p-V und T-s-Diagramm
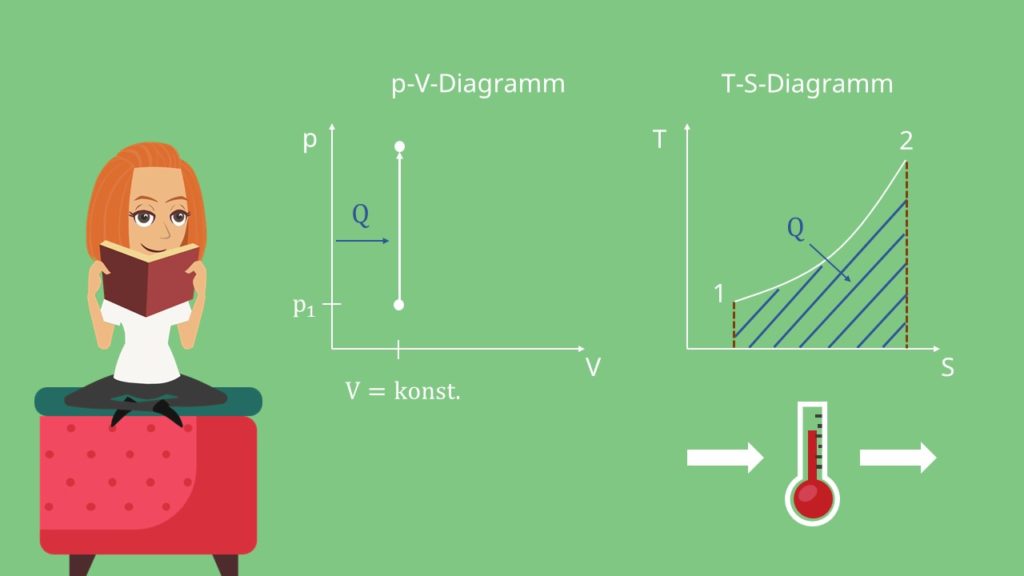
Schauen wir uns nun das p-V-Diagramm und das T-s-Diagramm an.
Im p-V-Diagramm verläuft die Zustandskurve wenig überraschend vertikal bzw. parallel zur p-Achse (vertikale Achse). Bei isochoren Zustandsänderungen bleibt das Volumen schließlich konstant, es gilt v = const.
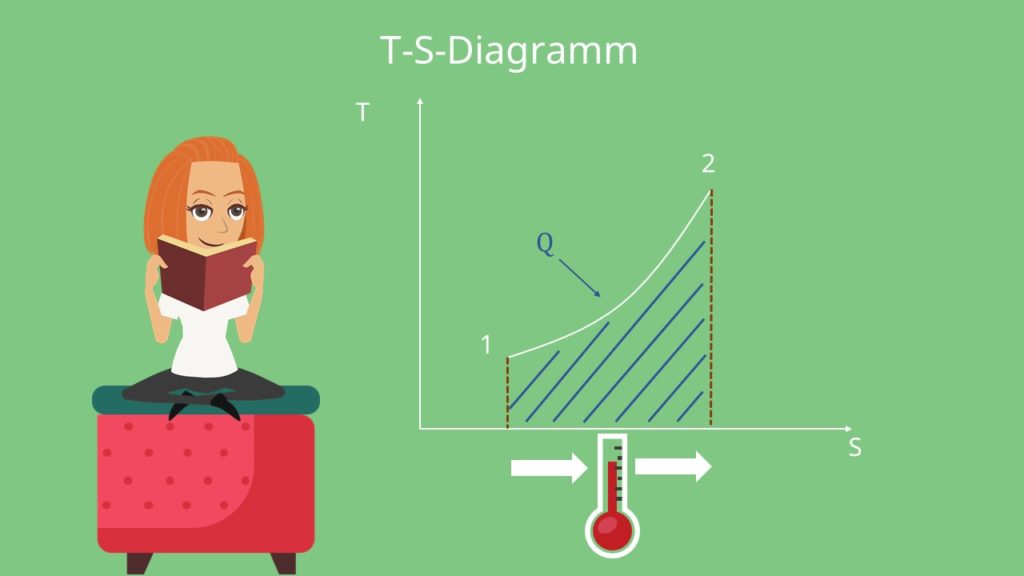
Im T-s-Diagramm stellt sich ein exponentieller Verlauf ein.
Berechnung der Volumenarbeit
Bei der isochoren Zustandsänderung findet keine Volumenänderungsarbeit statt, da das Volumen konstant ist und sich nicht ändert. Daher gilt für den Term der Volumenänderungsarbeit folgendes:
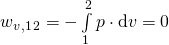
Wir könnten die Volumenänderungsarbeit im p-V-Diagramm grafisch darstellen. Dabei würde die Fläche unter der Kurve zur V-Achse (horizontalen Achse) diese Arbeit beschreiben. Da die Isochore im p-V-Diagramm aber als Senkrechte dargestellt wird, existiert auch keine Fläche und die Volumenänderungsarbeit ist somit gleich null.
Druckänderungsarbeit
In einem offenen System mit konstantem Volumen (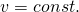 ) ergibt sich für die technische Arbeit (oder auch Druckänderungsarbeit):
) ergibt sich für die technische Arbeit (oder auch Druckänderungsarbeit):
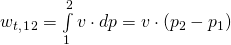
Setzt man in diese Gleichung die thermische Zustandsgleichung ein, erhält man:
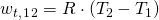
Auch die Druckänderungsarbeit können wir im p-V-Diagramm grafisch darstellen. Diese entspricht dabei der Fläche zwischen dem Graph und der p-Achse (der vertikalen Achse).
Wärme
Betrachten wir nun den Wärmetransfer 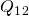 der isochoren Zustandsänderung. Die Formel für die innere Energie für ein geschlossenes System lässt sich wie folgt darstellen:
der isochoren Zustandsänderung. Die Formel für die innere Energie für ein geschlossenes System lässt sich wie folgt darstellen:
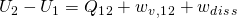
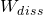 beschreibt dabei die bei irreversiblen Prozessen relevante Dissipationsarbeit. Bei reversiblen Prozessen gilt
beschreibt dabei die bei irreversiblen Prozessen relevante Dissipationsarbeit. Bei reversiblen Prozessen gilt 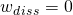 . Wie wir oben festgestellt haben, ist bei der isochoren Zustandsänderung die Volumenänderungsarbeit gleich null, deswegen folgt für die Wärme
. Wie wir oben festgestellt haben, ist bei der isochoren Zustandsänderung die Volumenänderungsarbeit gleich null, deswegen folgt für die Wärme 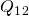 :
:
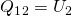 –
– 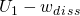
oder
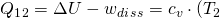 –
– 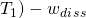 (für irreversiblen Prozess)
(für irreversiblen Prozess)
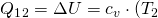 –
– 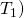 (für reversiblen Prozess)
(für reversiblen Prozess)
oder
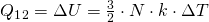
(mit N = Anzahl der Teilchen, k = Boltzmann-Konstante,  = Temperaturdifferenz)
= Temperaturdifferenz)
Die Fläche zwischen dem Graphen und der s-Achse (horizontale Achse) im T-s-Diagramm entspricht der zugeführten Wärmeenergie.
Entropie
Die Ausgangsformel für die Entropieänderung mit v = const. lautet:
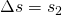 –
– 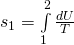
Schauen wir uns nun die Entropieänderung genauer an und integrieren die eben erhaltene Gleichung, können wir damit die Entropieänderung berechnen:
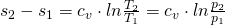
Fassen wir kurz zusammen, was wir gelernt haben. Bei der isochoren Zustandsänderung bleibt das Volumen konstant. Daher ist die Zustandskurve im p-V-Diagramm eine Gerade. Es wird nur Wärmeenergie transportiert und keine Volumenänderungsarbeit verrichtet. Außerdem können wir die Druck- und Volumenänderungsarbeit sowie die Wärmezufuhr im p-V- und T-s-Diagramm nachvollziehen.