Joule Prozess
Der Joule Prozess, auch Brayton Prozess genannt, ist einer von vielen thermodynamischen Kreisprozessen . Wir erklären dir anhand einer Gasturbine, was bei diesem abläuft.
Inhaltsübersicht
Gasturbinenprozess
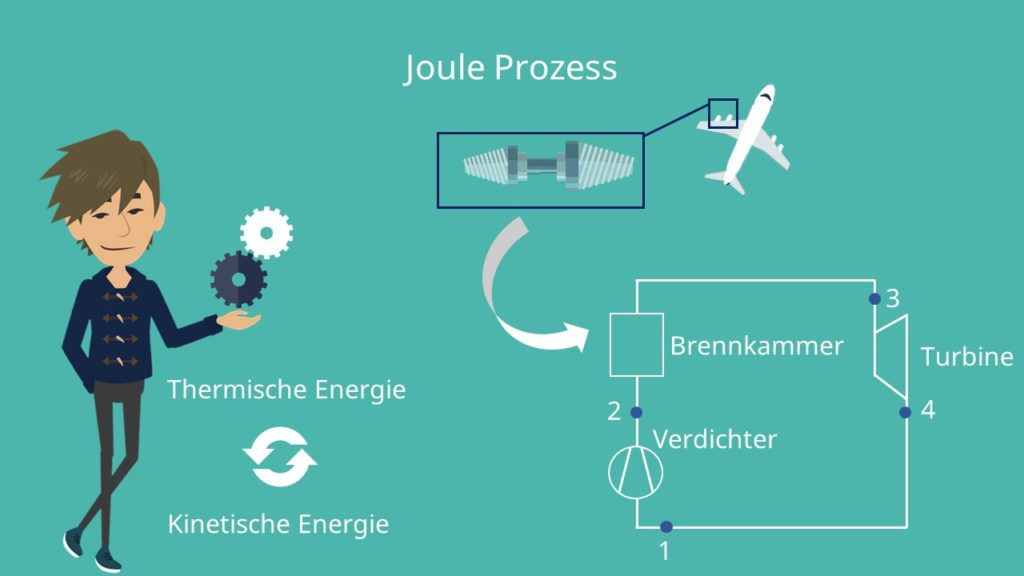
Ein gutes Beispiel für eine Umwandlung thermischer Energie in kinetische Energie ist die Gasturbine. Diese wird oft in Triebwerken von Flugzeugen, aber auch zur Gewinnung von technischer Leistung verwendet. Eine Gasturbine besteht aus einem Verdichter, einer Brennkammer, einer Turbine und einem Kondensator.
Vorgehen beim Joule Kreisprozess
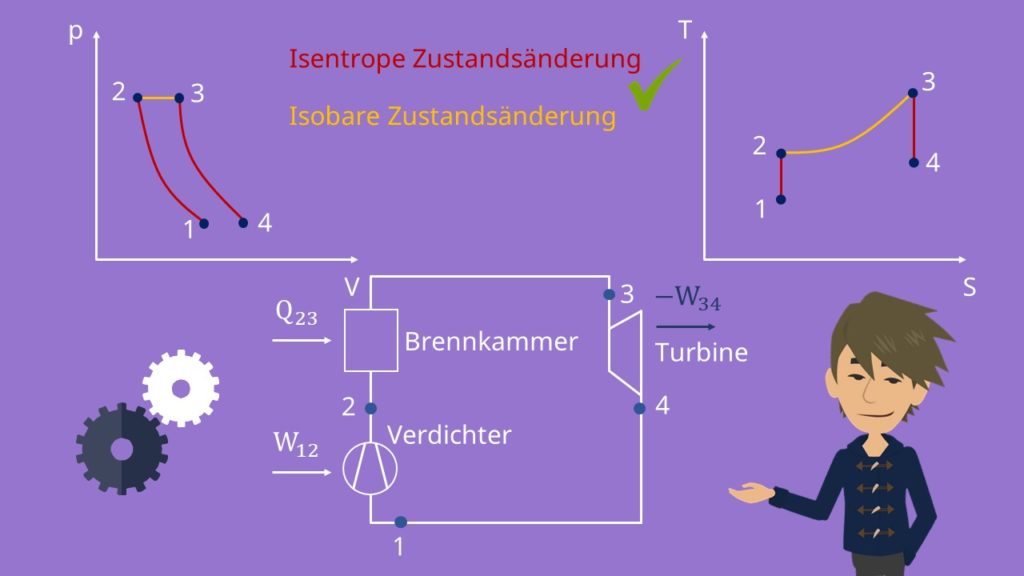
Schauen wir uns den Ablauf doch einmal im p-V- und T-S-Diagramm an.
Joule Prozess im p-V- und T-S-Diagramm
Die 4 Prozessschritte bzw. Takte beim Joule Prozess sind:
- Isentrope Kompression
- Isobare Wärmezufuhr
- Isentrope Expansion
- Isobare Wärmeabfuhr
Im Folgenden nehmen wir die einzelnen Prozessschritte genauer unter die Lupe:
Isentrope Kompression 1 -> 2:
Im Verdichter wird das Volumen der angesaugten Luft komprimiert. Dadurch steigt der Druck und das Volumen sinkt.
Die Temperatur erhöht sich durch die Kompression ebenfalls. Dieser Prozess läuft isentrop
, also ohne Wärmetransport ab (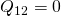 ). Daher ändert sich die Entropie
nicht (
). Daher ändert sich die Entropie
nicht (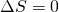 ).
).
Die Kompression des Gases wird durch Zuführung von Arbeit 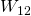 verrichtet.
verrichtet.
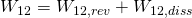
Da es sich um einen reversiblen, reibungsfreien Prozess handelt gilt 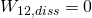 .
.
Isobare Expansion bzw. Wärmezufuhr 2 -> 3:
Als nächstes wird diese Luft in eine Brennkammer geleitet. Hier wird dann der Luft Brennstoff, zum Beispiel Dieselöl, Kerosin oder Petroleum, beigemischt und anschließend verbrannt. Dabei wird der Luft Wärmeenergie zugefügt. Das Volumen steigt, während der Druck konstant bleibt. Der Grund dafür ist, dass die Zustandsänderung isobar
abläuft. Durch die zugeführte Wärmeenergie steigen auch die Temperatur und die Entropie. Da der Druck konstant bleibt (dp = 0), gilt für die reversible technische Arbeit  .
.
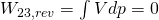
Isentrope Expansion 3 -> 4:
Die energiereiche Luft kommt als nächstes in die erwähnte Turbine. Hier soll wieder isentrop auf Umgebungsdruck entspannt werden. Das Gas dehnt sich aus und verrichtet dabei Arbeit 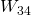 . Durch die Ausdehnung sinkt der Druck.
. Durch die Ausdehnung sinkt der Druck.
Im T-S-Diagramm fällt die Temperatur wieder ab.
Auch dieser Prozess läuft isentrop ab. Es wird also keine Wärme transportiert und die Entropie bleibt konstant. Die entstandene Arbeit wird in der Regel zum Teil genutzt, um den Verdichter anzutreiben, sodass nicht die gesamte Arbeit zur Verfügung steht. Dieser Prozess wird auch offener Joule-Prozess genannt.
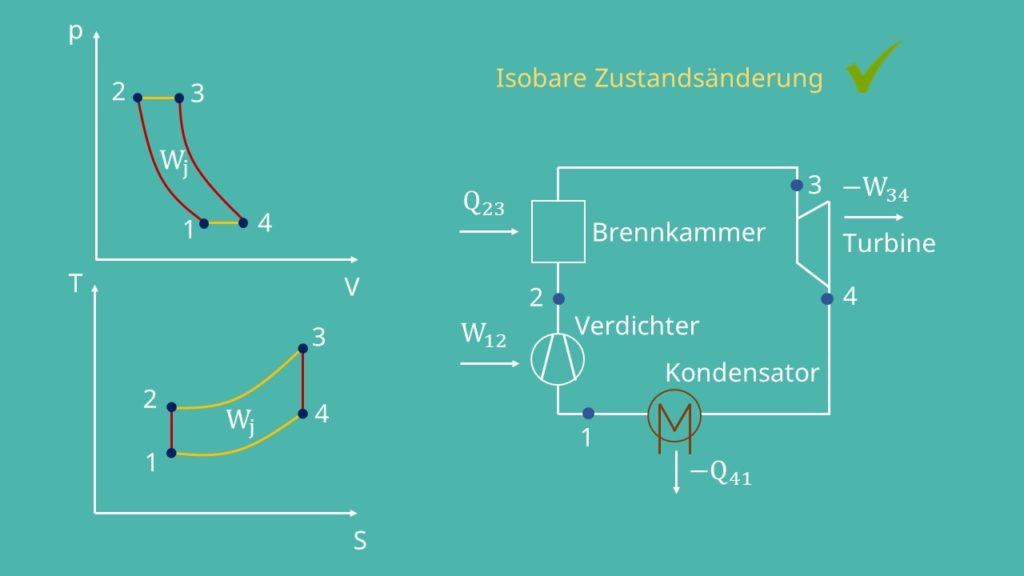
Der geschlossene Joule Prozess
Isobare Kompression bzw. Wärmeabfuhr 4 -> 1:
Natürlich gibt es auch einen geschlossenen Joule-Prozess. Hierfür bauen wir nach der Gasturbine einen Kühler bzw. Kondensator ein.
Das machen wir, weil der Verdichter immer mit dem gleichen Druck arbeiten soll. Da dieser von der Temperatur abhängt, können wir ihn über den Kühler regeln. Auf diese Weise lässt sich der Prozess optimieren. Dem Gas wird Wärmeenergie entzogen. In Folge dessen sinken die Temperatur und die Entropie. Das Ganze läuft wieder isobar ab, so dass der Druck konstant bleibt und das Volumen sinkt.
Gehen wir von der Realität aus, dann ist die Gasturbinenanlage ein offenes System. Das heißt für uns, dass wir uns den Kondensator wegdenken müssen. Für den Vergleichsprozess geht man aber von einem geschlossenen System aus.
Weitere Vergleichsprozesse:
Joule Prozess: Nutzarbeit
Der erste Hauptsatz der Thermodynamik lautet:
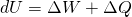
Nach dem Durchlaufen des Joule Prozesses stellen sich alle Zustandsgrößen auf ihren ursprünglichen Wert ein. Dementsprechend kann die zeitliche Änderung der inneren Energie gleich Null gesetzt werden (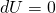 ). Für den Zusammenhang aus Arbeit W und Wärme Q gilt:
). Für den Zusammenhang aus Arbeit W und Wärme Q gilt:
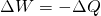
Die Nutzarbeit setzt sich aus der zugeführten und der abgeführten Wärme des Joule Prozesses zusammen. Die Nutzarbeit berechnet sich also wie folgt:
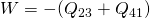
Joule Prozess: Thermischer Wirkungsgrad
Untersuchen wir nun, wie wir den Wirkungsgrad des Joule Prozesses berechnen können. Der Wirkungsgrad ist das Verhältnis von Nutzen zu Aufwand. In unserem Fall ist die abgegebene Arbeit der Nutzen und die zugeführte Wärme der Aufwand. Es folgt:
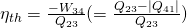
Der thermische Wirkungsgrad ist gleich der abgegebenen Arbeit durch die zugeführte Wärme oder anders ausgedrückt:
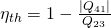
Eins minus den Betrag der abgeführten Wärme durch die zugeführte Wärme.
Wollen wir den Wirkungsgrad mit den Temperaturen berechnen, dann gilt:
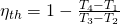
Super! Jetzt weißt du, wie du ganz einfach den Wirkungsgrad eines Joule Prozesses berechnen kannst. Du weißt auch, dass dieser in Gasturbinen stattfindet und aus zwei isentropen und zwei isobaren Zustandsänderungen besteht.