Klassifizierung partieller Differentialgleichungen
Partielle Differentialgleichungen sind ein wichtiges Thema im Maschinenbau. In diesem Beitrag erklären wir dir, was sie sind und in welche Klassen du sie einteilen kannst.
Inhaltsübersicht
Partielle DGL 2. Ordnung
Partielle Differentialgleichungen sind Differentialgleichungen, die zum Teil aus partiellen Ableitungen bestehen. Du kannst sie zum Beispiel benutzen, um physikalische Vorgänge mathematisch darzustellen. Zu Beginn musst du erst einmal lernen, wie du partielle Differentialgleichungen zweiter Ordnung klassifizierst. Liegt dir eine partielle Differentialgleichung vor und ist sie linear und von zweiter Ordnung, dann kannst du ihren Typ bestimmen. Du erinnerst dich: Die höchste vorkommende Ableitung gibt die Ordnung deiner DGL an. Allgemein sieht eine partielle Differentialgleichung zweiter Ordnung so aus:
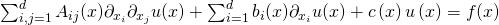
 steht für Dimension und gibt die Anzahl der Variablen an, von denen die Funktion u abhängt.
steht für Dimension und gibt die Anzahl der Variablen an, von denen die Funktion u abhängt.

Wenn  gleich zwei ist, ist
gleich zwei ist, ist  von zwei Variablen abhängig.
von zwei Variablen abhängig.
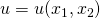
Kommen wir zurück auf die Darstellung der partiellen Differentialgleichung. 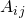 sind die Koeffizienten der zweiten Ableitungen,
sind die Koeffizienten der zweiten Ableitungen, 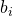 sind die Koeffizienten der ersten Ableitungen und c der Koeffizient der unabgeleiteten Funktion
sind die Koeffizienten der ersten Ableitungen und c der Koeffizient der unabgeleiteten Funktion 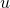 . Diese Koeffizienten können alle von den Variablen im Vektor
. Diese Koeffizienten können alle von den Variablen im Vektor 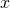 abhängen.
abhängen.
Allgemeine Schreibweise in zweidimensionale DGL umwandeln
Lass dich von den Summen und Indizes nicht verunsichern. Denn jetzt zeigen wir dir, wie du von der allgemeinen Schreibweise auf eine zweidimensionale Differentialgleichung übergehst.
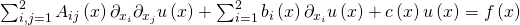
Zunächst schreiben wir die erste Summe aus. Dafür musst du für 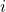 und
und 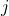 einfach Eins beziehungsweise Zwei einsetzen und alle Kombinationen durchgehen.
einfach Eins beziehungsweise Zwei einsetzen und alle Kombinationen durchgehen.

Wir schreiben diesen Teil mal etwas übersichtlicher, indem wir alle Abhängigkeiten in Klammern weglassen und die partiellen Ableitungen durch Indizes ersetzen.
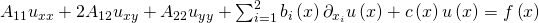
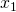 benennen wir um in
benennen wir um in 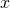 und
und 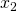 in
in  .
. 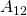 und
und 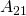 sind aufgrund des Satzes von Schwarz gleich.
sind aufgrund des Satzes von Schwarz gleich.
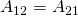
Auf die gleiche Art und Weise schreiben wir den Rest der Gleichung aus.
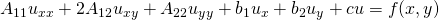
Sieht doch gar nicht mehr so schlimm aus! Um jetzt den Typ zu bestimmen, musst du die Koeffizienten 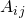 in einer Matrix zusammenfassen. Diese ist per Definition symmetrisch.
in einer Matrix zusammenfassen. Diese ist per Definition symmetrisch.
![Rendered by QuickLaTeX.com \mathbit{A}=\left[\begin{matrix}A_{11}&A_{12}\\A_{12}&A_{22}\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c0aeb8bfcd10026122bd462753fac952_l3.png)
Die Koeffizienten 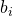 ergeben einen Vektor.
ergeben einen Vektor.
![Rendered by QuickLaTeX.com \mathbit{b}=\left[\begin{matrix}b_1\\b_2\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-753ccabaf6ca6d3c9f1244fe0e3822e4_l3.png)
Im nächsten Schritt bestimmst du die Eigenwerte von A.
Die Differentialgleichung ist elliptisch, wenn A positiv definit ist, also alle Eigenwerte positiv sind. Sie ist hyperbolisch, wenn alle Eigenwerte außer einem positiv sind und der übrige Eigenwert negativ ist. Die Differentialgleichung ist parabolisch, wenn alle Eigenwerte von A außer einem positiv sind und der letzte Eigenwert gleich Null ist. Außerdem muss die Matrix ![Rendered by QuickLaTeX.com \left[\mathbit{A}\middle|\mathbit{b}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d3d68998a5c679a4a4400327e0a866e0_l3.png) vollen Rang haben. Diese Überprüfung wird oft vergessen.
vollen Rang haben. Diese Überprüfung wird oft vergessen.
Beispiele
Jetzt wollen wir uns mal ein paar Beispiele ansehen. Zunächst schauen wir uns die Poisson-Gleichung an:
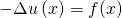
Das Dreieck ist der Laplace-Operator. Er ist wie folgt definiert:

Die zweiten Ableitungen nach allen Variablen im Vektor x werden summiert. Im Zweidimensionalen sieht die Poisson-Gleichung so aus:
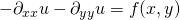
Von dieser wollen wir die Matrix A bestimmen:
![Rendered by QuickLaTeX.com \mathbit{A}=\left[\begin{matrix}-1&0\\0&-1\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dcddcc62d60c678679be8c50cd3d42cc_l3.png)
Der Vorfaktor der zweiten Ableitung nach x kommt an die Stelle Eins Eins der Matrix und der Vorfaktor der zweiten Ableitung nach y an die Stelle Zwei Zwei. Gemischte Ableitungen kommen nicht vor, so dass wir an den restlichen Stellen Nullen eintragen. Es ergibt sich eine Diagonalmatrix, so dass wir die Eigenwerte einfach ablesen können. Beide Eigenwerte haben den Wert minus Eins und sind damit negativ. Folglich wäre die Differentialgleichung keine der drei Typen. Man hätte die DGL aber auch schon zu Beginn mit minus Eins durchmultiplizieren können und dann durch aufstellen von A die Einheitsmatrix erhalten.
Diese hat die positiven Eigenwerte Eins und Eins. Die Poisson-Gleichung ist also elliptisch. Im Zweidimensionalen kannst du auch an der Determinante sehen, welcher Typ vorliegt.
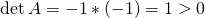
Ist die Determinante positiv, ist die Differentialgleichung elliptisch. Das kann dir helfen, wenn du keine einfache Diagonalmatrix hast.
Eindimensionale Wärmeleitungsgleichung
Als Nächstes nehmen wir uns die eindimensionale Wärmeleitungsgleichung vor. Als zweite Dimension kommt jetzt noch die Zeit ins Spiel.
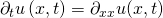
Wir stellen die Gleichung etwas um

und stellen die Matrix A auf.
![Rendered by QuickLaTeX.com A=\left[\begin{matrix}1&0\\0&0\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4ccbfbe91b7117da8806f1d430cb2198_l3.png)
Es kommt nur die zweite Ableitung nach x vor, also tragen wir eine Eins ein. Es gibt aber keine zweite Ableitung nach t oder gemischte Ableitungen. Folglich füllen wir die Matrix mit Nullen auf. Es ergibt sich wieder eine Diagonalmatrix, sodass wir die Eigenwerte Eins und Null ablesen können. Diese Eigenwerte deuten darauf hin, dass die Differentialgleichung parabolisch ist. Bei parabolischen Differentialgleichungen musst du noch prüfen, ob die zusammengesetzte Matrix ![Rendered by QuickLaTeX.com \left[\mathbit{A}\middle|\mathbit{b}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d3d68998a5c679a4a4400327e0a866e0_l3.png) vollen Rang hat. Dafür stellen wir b auf. Auch das kannst du aus der DGL ablesen, und zwar an den Vorfaktoren vor den ersten Ableitungen
vollen Rang hat. Dafür stellen wir b auf. Auch das kannst du aus der DGL ablesen, und zwar an den Vorfaktoren vor den ersten Ableitungen
![Rendered by QuickLaTeX.com b=\left[\begin{matrix}0\\-1\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1c2f48342c5c1b1be7f57faeadb674cc_l3.png)
Es wird einfach nach t abgeleitet, aber nicht nach x. Die Matrix ![Rendered by QuickLaTeX.com \left[\mathbit{A}\middle|\mathbit{b}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d3d68998a5c679a4a4400327e0a866e0_l3.png) sieht also so aus
sieht also so aus
![Rendered by QuickLaTeX.com \left[\mathbit{A}\middle|\mathbit{b}\right]=\left[\begin{matrix}1&0&0\\0&0&-1\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-972edcb44718029e98e99ba16e83f6d9_l3.png)
Die Zeilen sind linear unabhängig und damit hat die Matrix vollen Rang. Also ist die Wärmeleitungsgleichung parabolisch. Für 2×2-Matrizen parabolischer Differentialgleichungen ist übrigens die Determinante gleich Null.
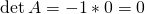
Das ist hier der Fall. Aber du hättest danach dennoch den Rang der ![Rendered by QuickLaTeX.com \left[\mathbit{A}\middle|\mathbit{b}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d3d68998a5c679a4a4400327e0a866e0_l3.png) -Matrix überprüfen müssen.
-Matrix überprüfen müssen.
Eindimensionale Wellengleichung
Als letztes schauen wir uns die eindimensionale Wellengleichung an. Diese ist ebenso von der Zeit t abhängig.
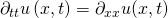
Wir stellen die Gleichung um
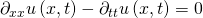
Und bestimmen die A-Matrix
![Rendered by QuickLaTeX.com \mathbit{A}=\left[\begin{matrix}1&0\\0&-1\\\end{matrix}\right]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-550fe7abc830382e04e04fdde173be55_l3.png)
Die Eigenwerte stehen auch hier auf der Diagonalen. Es sind Eins und minus Eins und damit ist die Wellengleichung hyperbolisch. Alternativ hättest du auch hier die Determinante bestimmen können, da die A-Matrix eine 2×2-Matrix ist.

Sie ist negativ. Auch daraus hättest du folgern können, dass die Differentialgleichung hyperbolisch ist.
Fassen wir die Kriterien noch einmal zusammen. Die Matrix A elliptischer Differentialgleichungen hat nur positive Eigenwerte, sie ist also positiv definit. Die Determinante der A-Matrix ist größer Null, wenn es eine Zwei-Kreuz-Zwei-Matrix ist und ein Beispiel für eine elliptische Gleichung ist die Poisson-Gleichung. Hyperbolische Differentialgleichungen haben d minus Eins positive und einen negativen Eigenwert, sodass die A-Matrix indefinit ist. Im Zweidimensionalen ist die Determinante kleiner Null. Ein Beispiel ist die Wellengleichung. Parabolische DGLs haben d minus Eins positive Eigenwerte und einen Eigenwert gleich Null. Damit sind sie positiv semidefinit und die Determinante ist gleich Null. Außerdem musst du prüfen, ob die Matrix A b vollen Rang hat. Ein Beispiel ist die Wärmeleitungsgleichung.
Jetzt weißt du, wie du partielle DGLs in elliptische, hyperbolische und parabolische Differentialgleichungen einteilst. In den nächsten Beiträgen lernst du die verschiedenen Typen zu lösen.



