Maschenstromverfahren
In diesem Beitrag erklären wir dir eine Möglichkeit für die Netzwerkanalyse, das sogenannte Maschenstromverfahren. Damit kannst du Ströme und Spannungen in komplexen Schaltungen berechnen. Wir zeigen dir wie du von deiner Schaltung, zu einer Matrix kommst und wie du sie anschließend löst.
In unserem Video erklären wir dir wie du dabei Schritt für Schritt vorgehst. Also schau doch mal rein.
Inhaltsübersicht
Maschenstromverfahren einfach erklärt
Das Maschenstromverfahren ist ein Verfahren zur Netzwerkanalyse von komplexeren Schaltungen. Für dieses Verfahren werden Hilfsgrößen definiert: die sogenannten Maschenströme. Sie fließen kreisförmig in den zuvor definierten Maschen. Die Maschenströme berechnest du, indem du ein lineares Gleichungssystem in Matrixform aufstellst und anschließend löst. Schließlich kannst du deine gesuchte Ströme aus den Maschenströmen berechen. Im folgenden zeigen wir dir detailliert wie du dabei vorgehst.
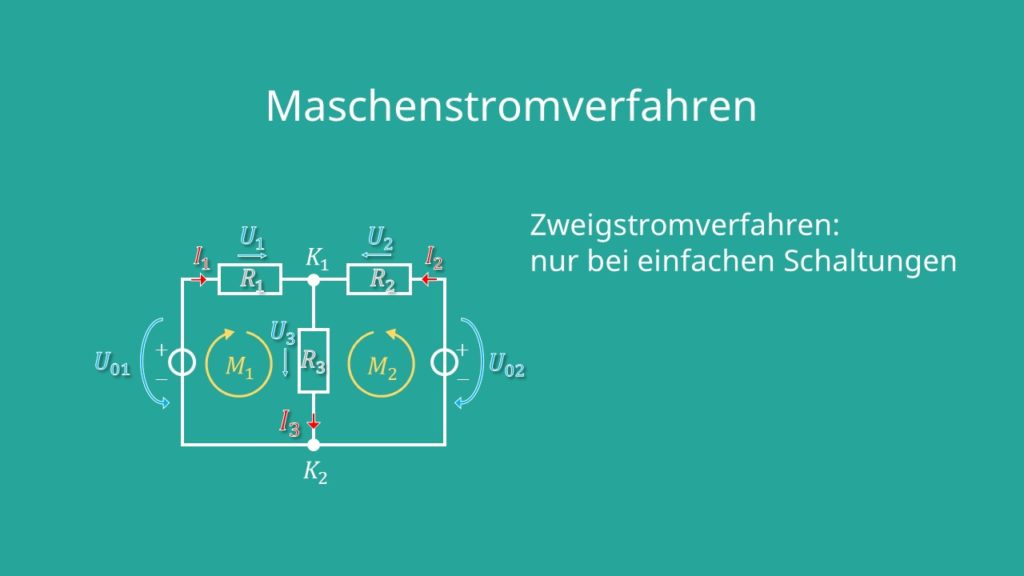
Maschenströme Definition
Maschenströme sind rein formale Größen, sie werden also nur angenommen, um die Berechnung zu vereinfachen. Anhand folgender Schaltung kannst du dir die Maschenströme veranschaulichen. Hier gibt es zwei Maschen 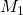 und
und 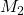 , mit den jeweils zugehörigen Maschenströmen
, mit den jeweils zugehörigen Maschenströmen 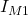 und
und 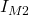 .
.
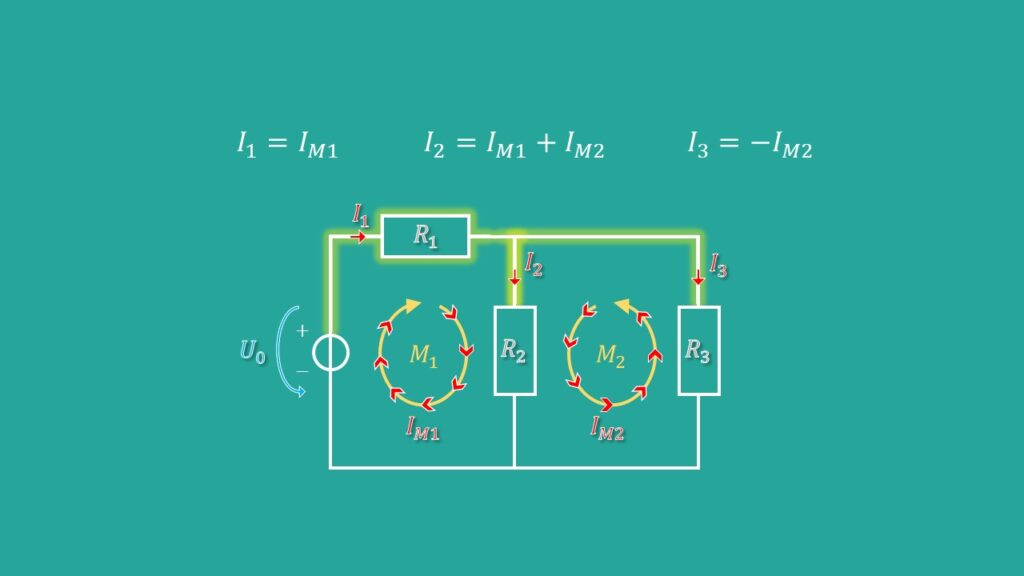
An den Stellen, an denen ein Zweig nur zu einer einzigen Masche gehört, ist der Maschenstrom identisch mit dem jeweiligen Zweigstrom.
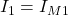 und
und 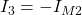
Dort, wo ein Zweig zu zwei Maschen gehört, überlagern sich die Maschenströme: der wahre Zweigstrom ist dann die Summe der einzelnen Maschenströme.
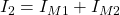
Natürlich spielt hier auch die Richtung der definierten Maschen eine Rolle und äußert sich mit einem negativen Vorzeichen, wenn Maschen- und Zweigstrom nicht in die gleiche Richtung zeigen. Diese drei Regeln sind immer dann erlaubt, wenn in deiner Schaltung ein linearer Zusammenhang zwischen Strom und Spannung herrscht, also das Ohmsche Gesetz gilt.
Maschenstromverfahren Beispiel
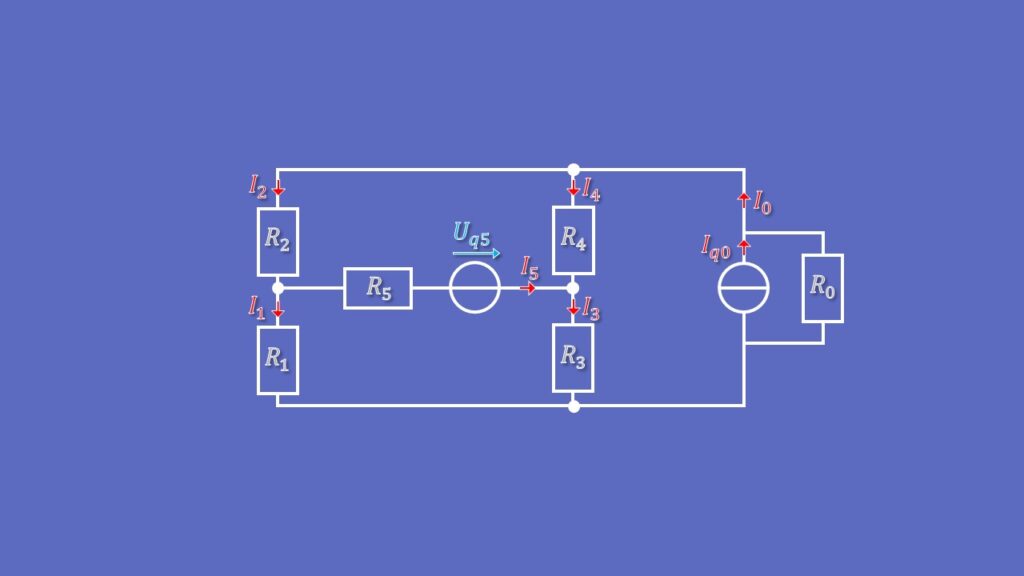
Schauen wir uns die einzelnen Schritte des Maschenstromverfahrens nun an einem Beispiel genauer an. Wir betrachten folgende Schaltung, bei der die einzelnen Ströme unbekannt sind.
Wir suchen I0, I1, I2, I3, I4 und I5.
Wenn du dieses Netzwerk mit dem Maschenstromverfahren analysieren möchtest, musst du folgende Schritte abarbeiten:
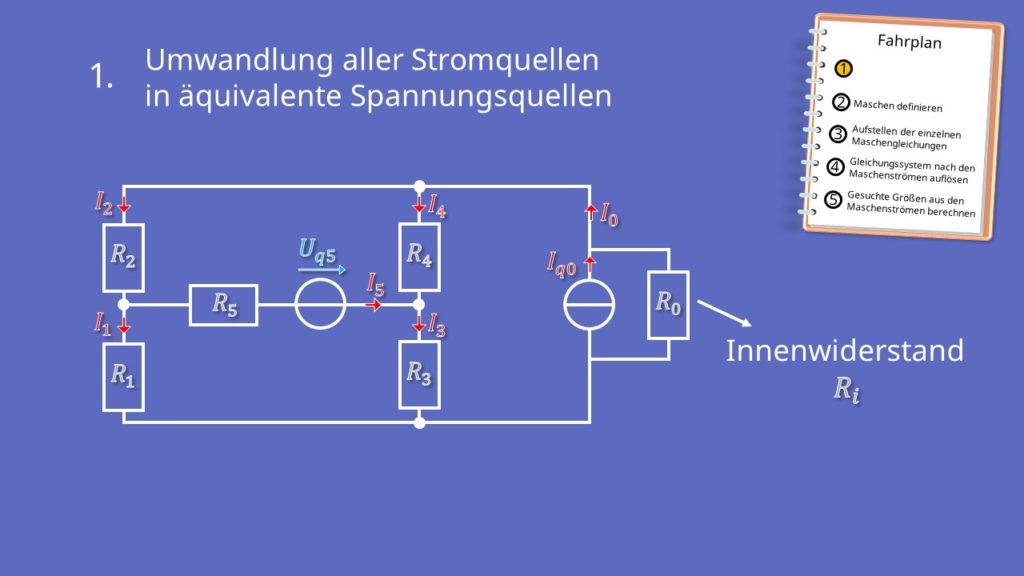
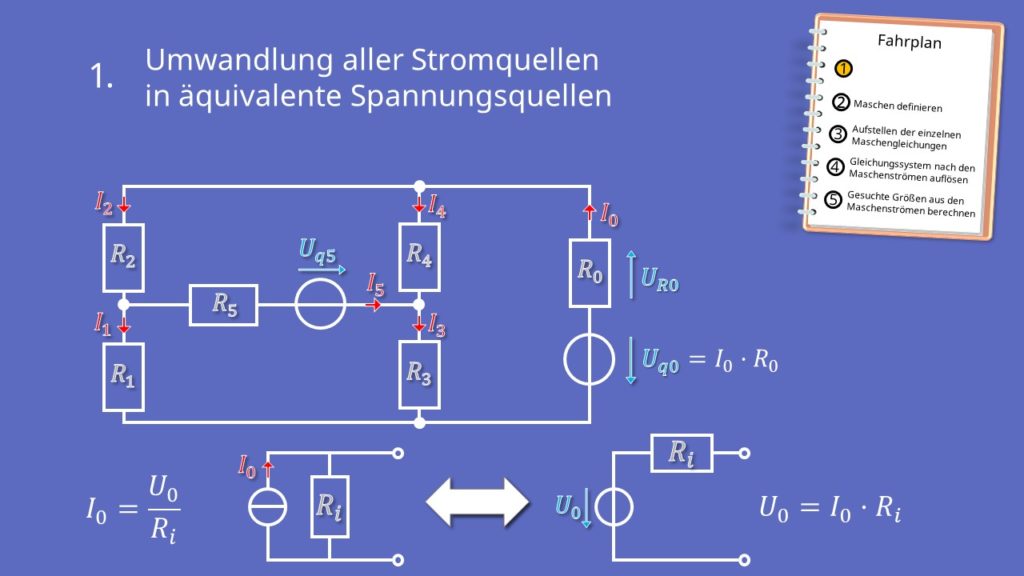
- Umwandlung aller Stromquellen in äquivalente Spannungsquellen.
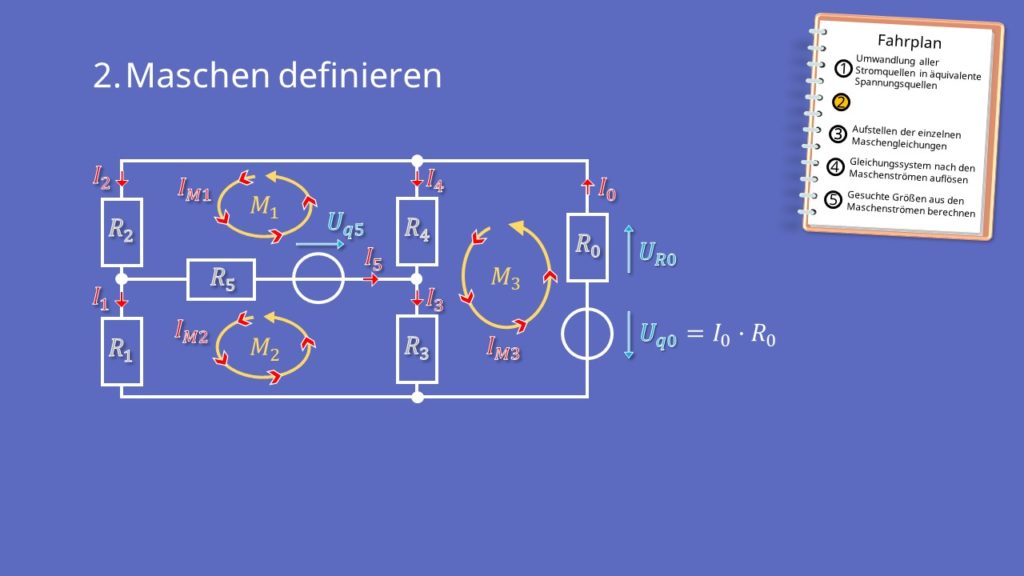
- Maschen definieren. In jeder Masche fließt kreisförmig ein zugehöriger Maschenstrom.
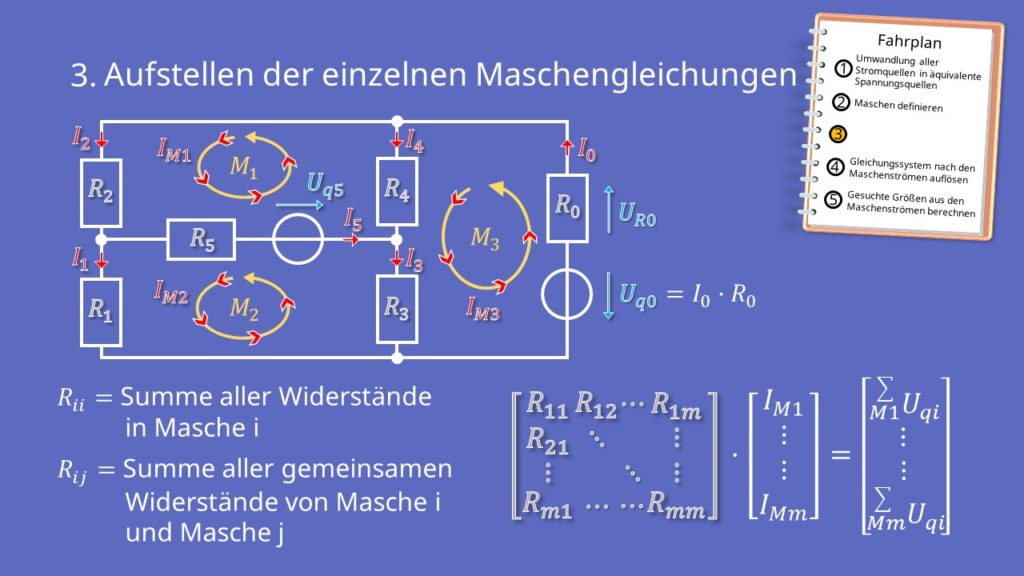
- Aufstellen der einzelnen Maschengleichungen
- Gleichungssystem nach den Maschenströmen auflösen und
- Gesuchte Größen aus den Maschenströmen berechnen.
Umwandlung der Stromquellen in Spannungsquellen
Kommen wir zu Schritt eins:
In der Schaltung gibt es nur eine Stromquelle, die in eine Spannungsquelle umgewandelt werden muss. 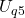 ist bereits eine Spannungsquelle.
ist bereits eine Spannungsquelle.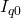 ist eine Stromquelle und muss jetzt in eine Spannungsquelle umgewandelt werden. Der Widerstand
ist eine Stromquelle und muss jetzt in eine Spannungsquelle umgewandelt werden. Der Widerstand 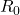 stellt den Innenwiderstand der Stromquelle dar.
stellt den Innenwiderstand der Stromquelle dar.
Für die Umwandlung der Stromquelle in eine Spannungsquelle gehst du nach folgendem Schema vor:
Die Spannung der nun erzeugten Spannungsquelle berechnest du mit:
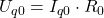
Ihr Innenwiderstand 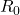 liegt nun in Reihe zur Spannungsquelle.
liegt nun in Reihe zur Spannungsquelle.
Definition der Maschen
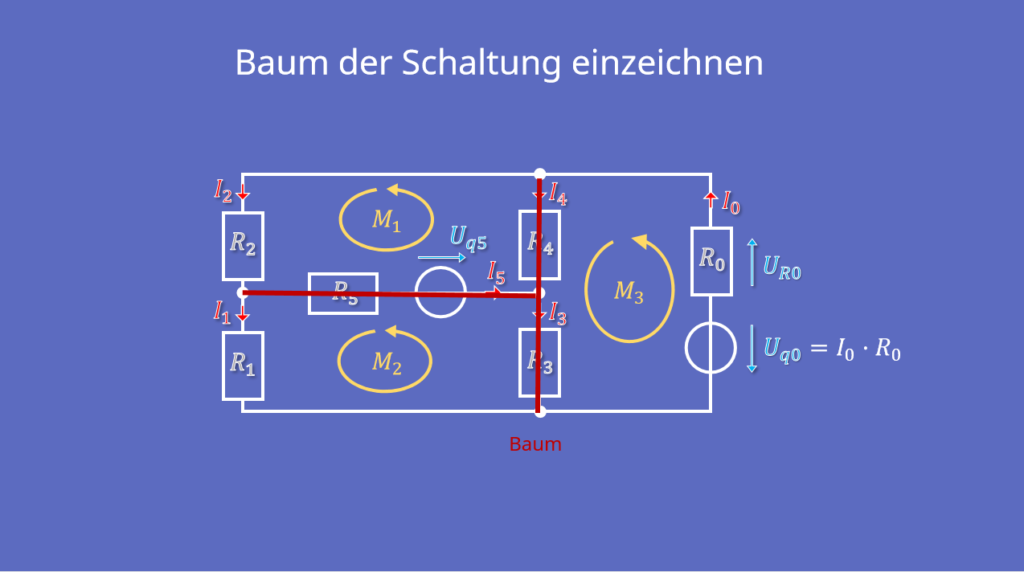
Um die erforderlichen Maschen für das Maschenstromverfahren zu ermitteln, ist es erforderlich einen sogenannten Baum der Schaltung zu bestimmen. Genauer kannst du dich auch in unserem Video zu linear unabhängigen Maschen informieren.
Der Begriff Baum stammt aus der Graphentheorie, er verbindet alle Knoten einer Schaltung ohne einen Umlauf zu beinhalten. In der Regel können in einer Schaltung mehrere verschiedene Bäume gefunden werden. Jeder von Ihnen kann für das Maschenstromverfahren heranzogen werden. Wird ein Baum über die sogenannten Verbindungszweige geschlossen, so entstehen immer linear unabhängige Maschen. Die so ermittelten Maschen werden für die anschließenden Schritte verwendet.
Die Richtung der Maschen kann frei gewählt werden. In Masche 1 fließt kreisförmig der zugehörige Maschenstrom IM1, in Masche 2 IM2 und Masche 3 IM3. Üblicherweise fließt der Maschenstrom in Maschenrichtung.
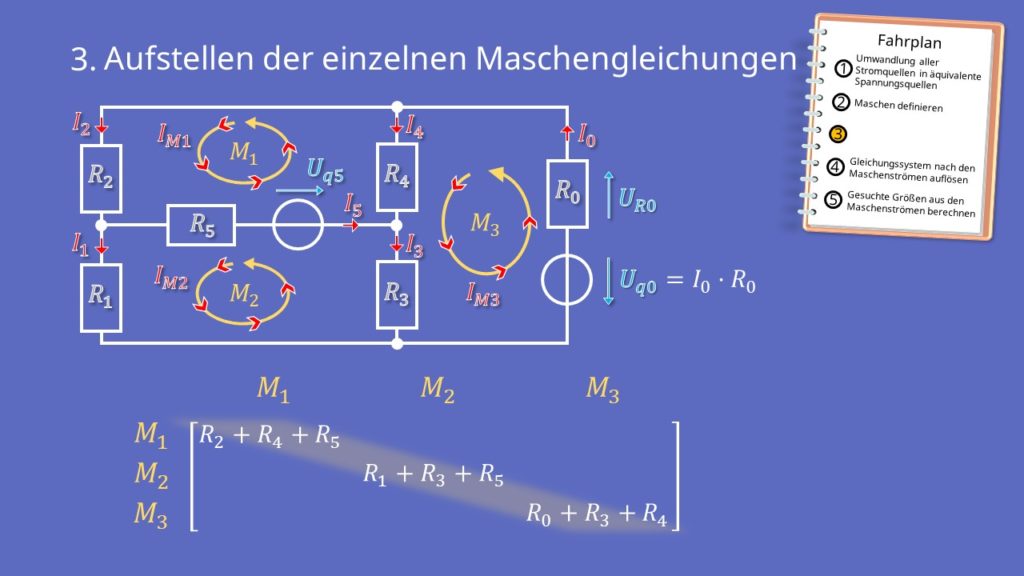
Aufstellen der Maschengleichungen
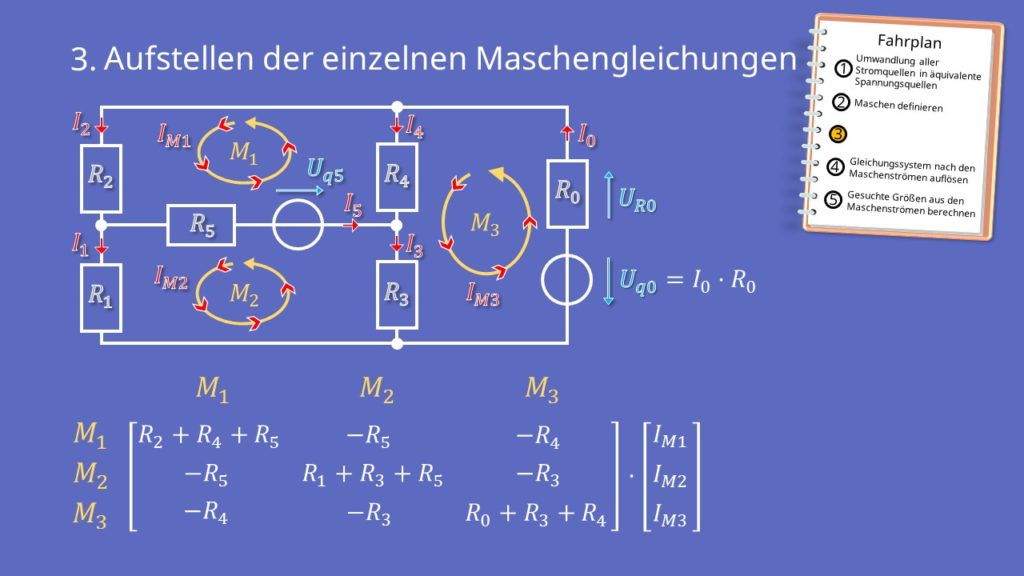
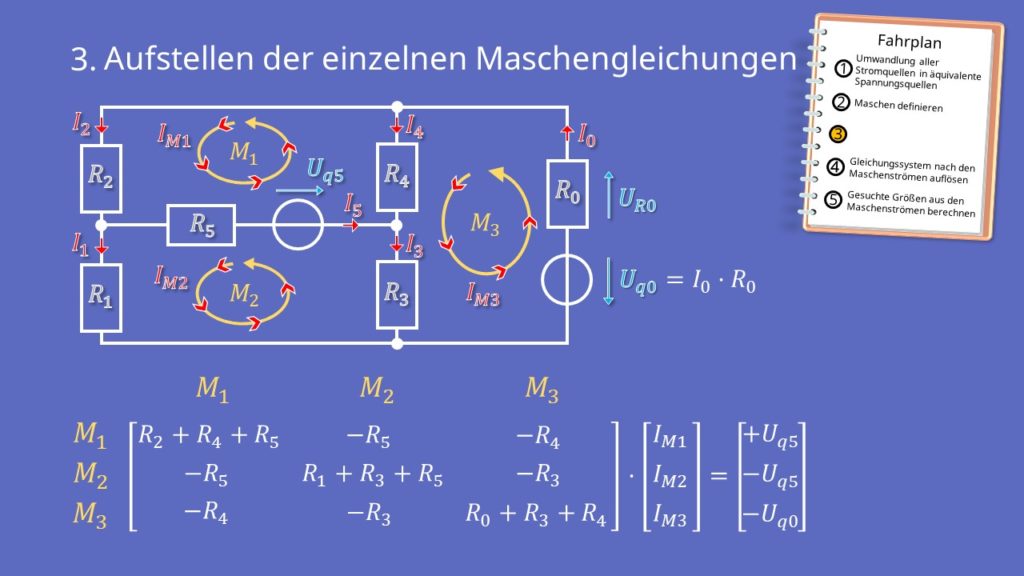
Das Aufstellen der Maschengleichungen ist ein wichtiger Bestandteil des Maschenstromverfahrens. Wenn du hier schematisch vorgehst, dann ist das auch recht einfach. Das machst du am besten, indem du dir jede Masche einzeln betrachtet, und dann in eine Matrix schreibst. Das spart nicht nur Schreibarbeit, sondern ist auch besser zum Ausrechnen. In der Matrix bekommt jede Masche eine eigene Zeile.
Die Matrixschreibweise hat allgemein diese Form:
Rii ist dabei die Summe aller Widerstände in der Masche i. Rij ist die Summe aller gemeinsamen Widerstände von Masche i und Masche j.
Danach folgt ein Vektor mit den einzelnen Maschenströmen IM1 bis IMm für die m-te Masche. Der Ergebnisvektor hinter dem Gleichheitszeichen ist die Summe aller Spannungsquellen in der jeweiligen Masche. Falls es in einer Masche keine Spannungsquelle gibt, dann steht hier eine Null.
Maschenstromverfahren Matrix
Starten wir mit dem Ausfüllen der Hauptdiagonalen der Matrix. Hier stehen die Summen aller Widerstände der jeweiligen Masche. Für das erste Element 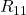 der Hauptdiagonalen ergibt sich dementsprechend die Summe der Widerstände in Masche 1.
der Hauptdiagonalen ergibt sich dementsprechend die Summe der Widerstände in Masche 1.
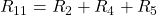
Für das zweite Element 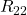 der Hauptdiagonalen ergibt sich:
der Hauptdiagonalen ergibt sich:
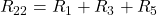
Und schließlich für das dritte Element 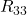 :
:
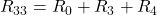
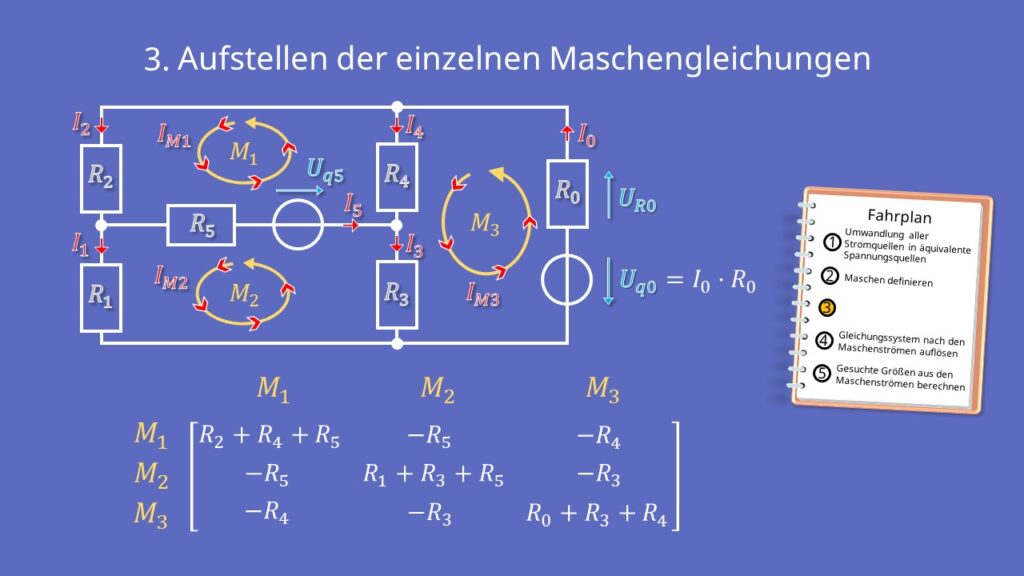
Nun schaust du welche Maschen Widerstände gemeinsam haben. Diese entsprechen den anderen Elementen der Matrix. Widerstand R4 kommt sowohl in Masche 1, als auch in Masche 3 vor. Entsprechend wird er als Matrixelement 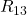 und
und 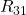 berücksichtigt.
berücksichtigt.
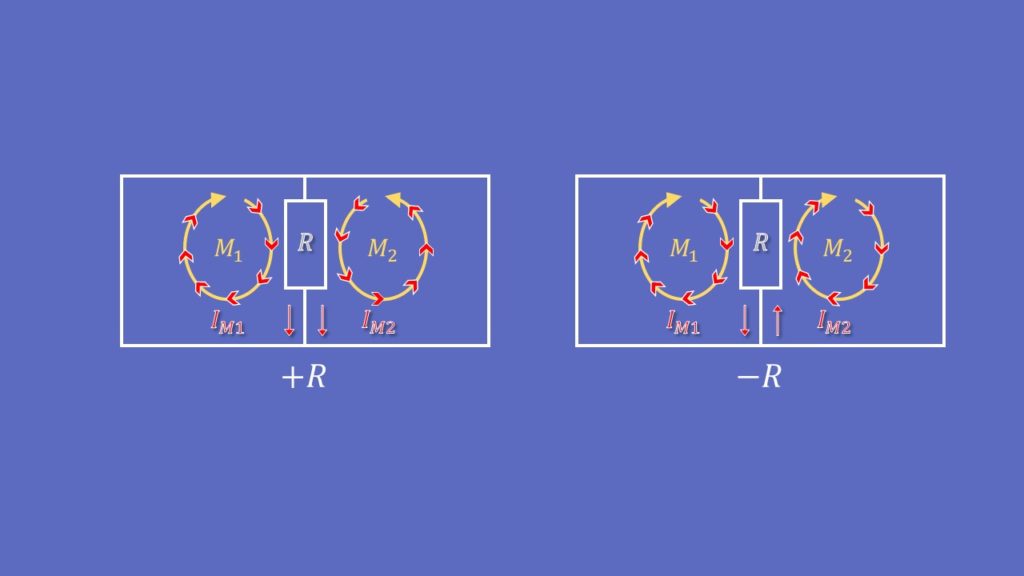
Hier musst du das Vorzeichen beachten. Zeigen die Maschenströme an dem Widerstand in die gleiche Richtung, so ist das Vorzeichen positiv, zeigen sie in eine entgegengesetzte Richtung, dann ist das Vorzeichen negativ.
Folglich ergibt sich:
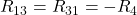
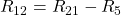
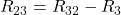
Anschließend wird noch der Vektor mit den Maschenströmen 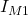 ,
,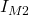 und
und 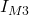 ergänzt.
ergänzt.
Berücksichtigung von Spannungsquellen
In unserem Beispiel kommen in allen drei Maschen Spannungsquellen vor. Sie werden im Ergebnisvektor berücksichtigt. An Erster Stelle steht die Summe der Spannungsquellen aus Masche 1, an zweiter Stelle die Summe der Spannungsquellen aus Masche 2 usw.. Auch hier musst du wieder auf das Vorzeichen achten.
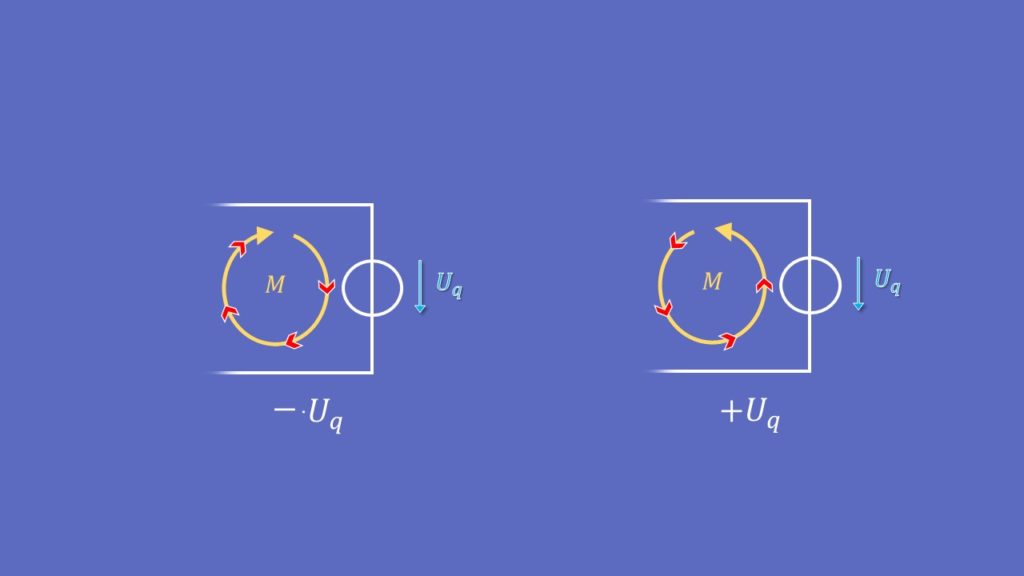
Ausschlaggebend ist dabei die Richtung der Spannungsquelle im Vergleich zum jeweiligen Maschenstrom. Das Prinzip scheint zwar ähnlich zu den Widerständen, aber die Vorzeichenregel ist gerade umgekehrt. Falls die Spannungsquelle entgegengesetzt zum Maschenstrom zeigt, dann ist die Spannung positiv, andernfalls, also falls beides in die gleiche Richtung zeigt, ist die Spannung negativ.
Somit steht an erster Stelle 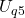 , an zweiter wiederum
, an zweiter wiederum 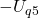 und an dritter Stelle dann minus
und an dritter Stelle dann minus 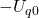 .
.
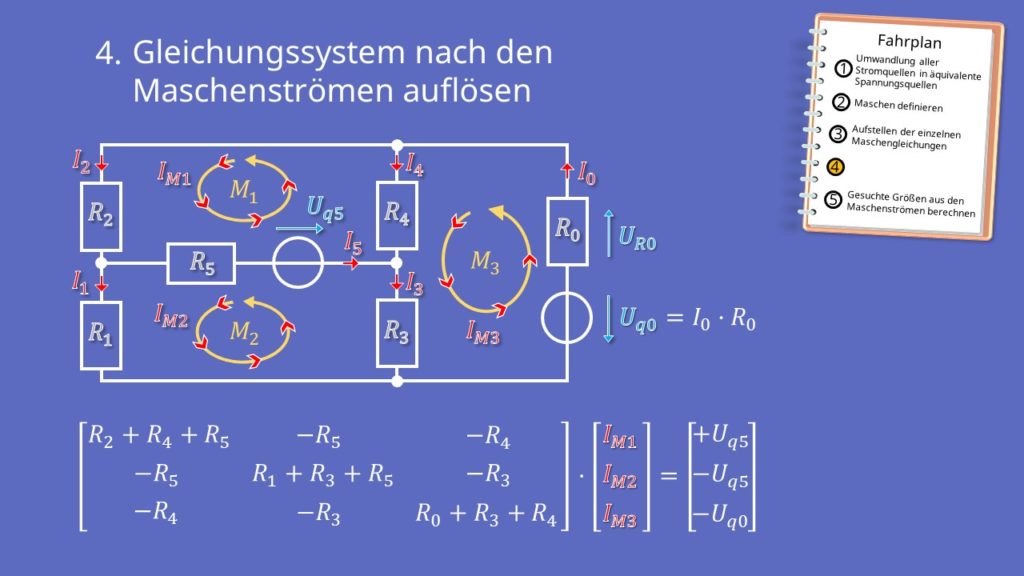
Auflösen nach den Maschenströmen
Nun kannst du IM1, IM2 und IM3 berechnen.
Dazu gibt es verschiedene Verfahren: Zum Beispiel die Cramersche Regel und das Gaußsche Eliminationsverfahren . An dieser Stelle werden wir diesen Schritt überspringen. Du kannst dir das genaue Vorgehen aber im Beitrag zur Cramerschen Regel beziehungsweise zum Gaußschen Eliminationsverfahren anschauen.
Berechnung der gesuchten Größen
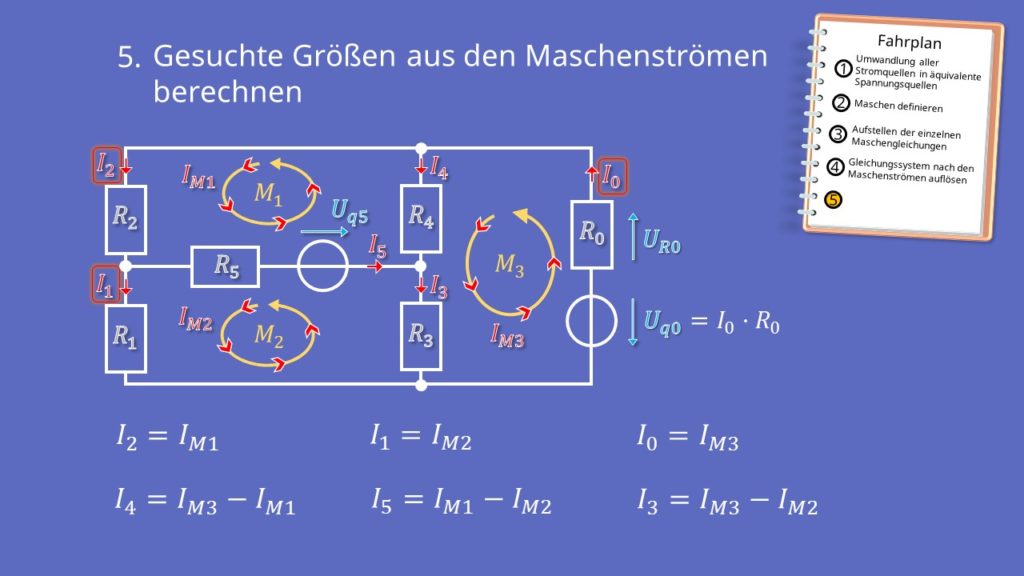
Im letzten Schritt des Maschenstromverfahrens kannst du die gesuchten Ströme aus den Maschenströmen berechnen.
Die Ströme I0, I1 und I2 kannst du direkt mit dem Maschenstrom ausdrücken, da sie an Stellen fließen, an denen der Zweig nur zu einer einzigen Masche gehört. In unserem Beispiel zeigen die Maschen in die gleiche Richtung wie diese Ströme. Daher sind sie alle positiv.
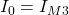
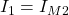
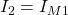
Die anderen Ströme setzen sich aus mehreren Maschenströmen zusammen. Ein im Vergleich zum Zweigstrom entgegengesetzt fließender Maschenstrom wird negativ und ein in die gleiche Richtung fließender Zweigstrom positiv berücksichtigt.
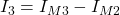
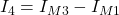
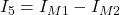
Damit haben wir mit Hilfe des Maschenstromverfahrens alle Unbekannten Ströme der Schaltung gefunden.