Massenbilanz
In diesem Artikel erklären wir dir anhand eines Alltagsbeispiels ganz unkompliziert, was es mit der Massenbilanz auf sich hat.
Inhaltsübersicht
Massenbilanz und Massenstrom
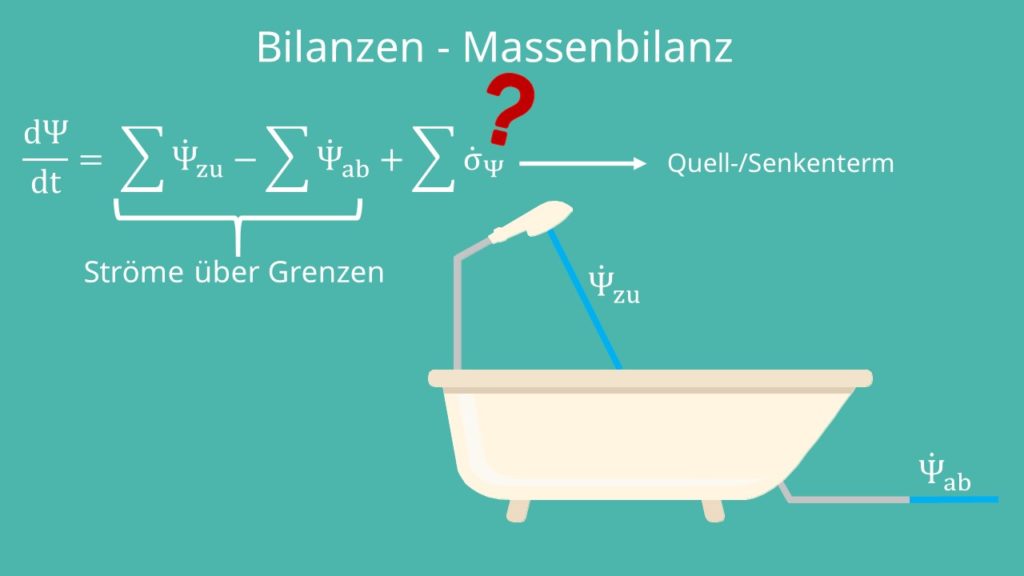
Bei Bilanzen betrachten wir eine gewisse Bilanzgröße in einem thermodynamischen System. Das kann die gesamte Masse oder Energie sein, aber auch zum Beispiel nur ein bestimmter Stoff. In der Regel betrachten wir dabei die zeitliche Änderung der jeweiligen Bilanzgröße. Allgemein hat die Bilanz für die Bilanzgröße 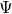 die Form:
die Form:
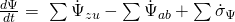
Das sieht jetzt noch sehr kompliziert aus. Es ist aber eigentlich ganz einfach. 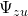 bzw.
bzw. 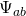 sind die Ströme über die Grenzen. Betrachten wir als Beispiel die Masse innerhalb einer Badewanne.
sind die Ströme über die Grenzen. Betrachten wir als Beispiel die Masse innerhalb einer Badewanne.
Der „Massenstrom zu“, ist das Wasser, das aus dem Wasserhahn kommt, während die abfließende Masse durch den Abfluss läuft. Und was ist jetzt das Sigma? Das ist ein sogenannter Quell- beziehungsweise ein Senken-Term. Dieser beschreibt, ob die Bilanzgröße im System verschwindet oder entsteht. Wenn du zum Beispiel ein Bier trinkst, scheidest du den ganzen Alkohol ja nicht wieder aus. Du setzt ihn um. Das heißt er „verschwindet“. Genau das stellt dieser Term da.
Allgemein gilt: Bilanzieren wir eine Erhaltungsgröße ist Sigma gleich Null. Die Gesamtmasse ist zum Beispiel eine Erhaltungsgröße. Das Wasser in der Badewanne verschwindet ja auch nicht einfach so.
Betrachten wir jetzt die Massenbilanz. Mit Sigma gleich Null erhalten wir:
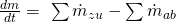
Um uns Arbeit beim Schreiben zu sparen, gibt es die Konvention, dass eintretende Bilanzgrößen, also das Wasser, das in die Badewanne, läuft positiv ist, und das abfließende negativ angenommen wird. Damit vereinfacht sich die Bilanz zu:
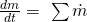
Massenbilanz der Badewanne berechnen
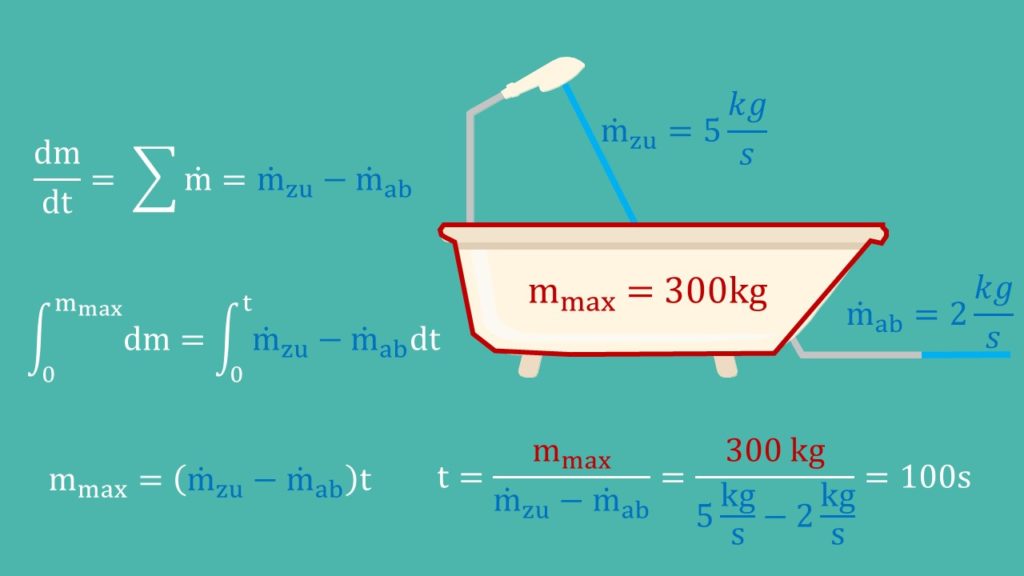
Nehmen wir jetzt an, in die Badewanne fließen fünf Kilogramm Wasser pro Sekunde hinein und zwei Kilogramm pro Sekunde hinaus. In die Badewanne passt eine Masse m max von 300 Kilogramm Wasser. Wir wollen jetzt wissen, wie lange es dauert, bis die Wanne überläuft. Wir setzen unsere Bilanzgrenzen genau um die Wanne. Stellen wir nun unsere Massenbilanz auf, erhalten wir:
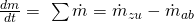
Um nun auf die Zeit zu kommen, müssen wir beide Seiten integrieren:
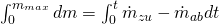
Damit erhalten wir eine einfache Formel:
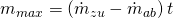
Das müssen wir jetzt nur noch nach t umformen und erhalten die Zeit:
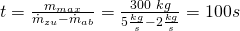
Bei den gegebenen Flüssen läuft die Badewanne also nach 100 Sekunden über.
Super, mithilfe der Massenbilanz kannst du so einfache Probleme schnell lösen.