Physikalisches Pendel
Dieser Artikel behandelt das Physikalische Pendel. Dabei liegt der Fokus vor allem auf dessen Bewegungsgleichung und einigen Sonderfällen. Ein praktischer Anwendungsfall des physikalischen Pendels liegt in der experimentellen Bestimmung der Massenträgheitsmomente beliebig geformter Körper.
Schon wieder so ein kompliziertes Thema? Unser Video erklärt dir das physikalische Pendel anschaulich innerhalb kürzester Zeit!
Inhaltsübersicht
Physikalisches Pendel einfach erklärt
Das physikalische Pendel wird auch als physisches Pendel, Trägheitspendel, Ausgleichspendel oder Minimalpendel bezeichnet. Es beschreibt anhand eines theoretischen Modells die Schwingung eines realen Pendels und besteht aus einem starren Körper, welcher nicht an seinem Schwerpunkt aufgehängt ist. Beim physikalischen Pendel werden Größe und die Form des Körpers berücksichtigt.
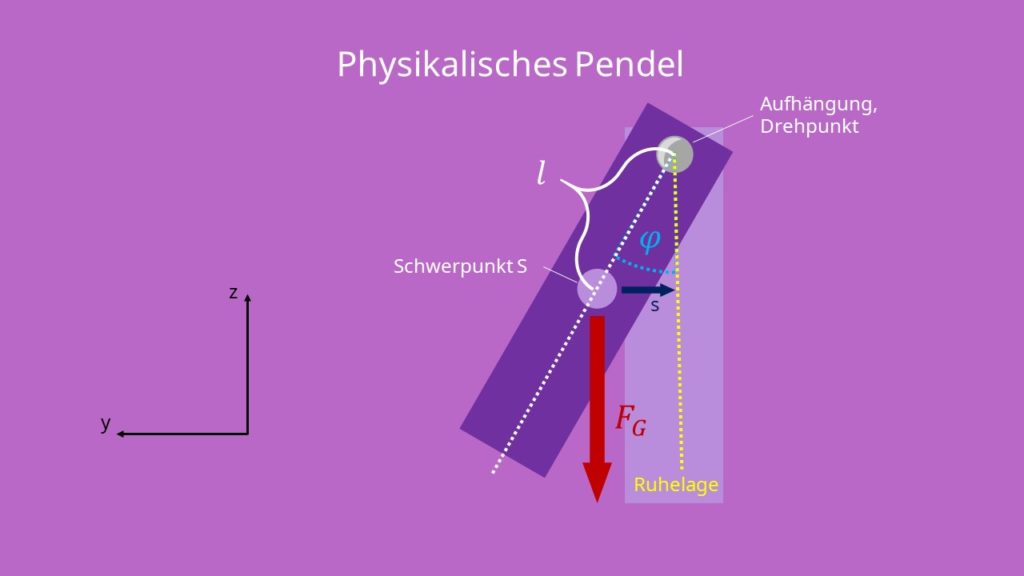
In der obigen Grafik haben wir ein Pendel in Ruhelage und in ausgelenkter Lage. Es befindet sich in der y, z-Ebene. Das Pendel ist an einer Aufhängung befestigt und hängt in der Ruhelage vertikal nach unten. L ist der senkrechte Abstand der Aufhängung zum Schwerpunkt. S ist der waagrechte Abstand des Schwerpunktes zum Bezugspunkt in der Ruhelage. Dabei beschreibt s ursprünglich eine Kreisbahn. Da der Winkel 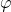 allerdings klein ist, kann es mit der Geraden angenähert werden.
allerdings klein ist, kann es mit der Geraden angenähert werden.
Der Schwerpunkt befindet sich dabei in der Ruhelage senkrecht unterhalb des Drehpunktes. In dem Beispiel oben, stellt die Aufhängung des Stabes auch den Drehpunkt dar. Die Summe aller Drehmomente und angreifenden Kräfte sind in der Gleichgewichtslage gleich Null.
Wird das physikalische Pendel ausgelenkt, beginnt es unter dem Einfluss der Schwerkraft harmonisch zu schwingen. Es wird ein rücktreibendes Drehmoment erzeugt, welches das Pendel zurück in die Gleichgewichtslage und darüber hinaustreibt. Der Pendelkörper ist grundsätzlich beliebig gelagert. Die Gewichtskraft G wirkt vom Schwerpunkt aus vertikal nach unten. Somit beschreibt der Winkel 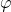 die Auslenkung des Stabes gegenüber seinem Ruhezustand.
die Auslenkung des Stabes gegenüber seinem Ruhezustand.
Es gilt das dynamische Grundgesetz für die Drehbewegung:
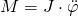
Das Rückstellmoment kann man mit Hilfe der Rückstellkraft und dem Abstand s aufstellen:
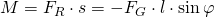
Somit erhält man:
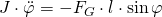
Für die rücktreibende Kraft gilt also analog:
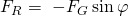
Diese greift im Schwerpunkt an und ist eine Teilkomponente der Gewichtskraft 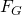 .
.
Damit wir ein physikalisches Pendel mit einer harmonischen Schwingung haben, muss die Auslenkung  minimal sein und der Luftwiderstand wird vernachlässigt.
minimal sein und der Luftwiderstand wird vernachlässigt.
Unterschied mathematisches und physikalisches Pendel
Das physikalische Pendel berücksichtigt im Gegensatz zum mathematischen Modell, sowohl die Größe als auch die Form des Pendelkörpers. Daher nähert es sich dem realen Pendel stärker an als das mathematische Modell.
Während das mathematische Pendel von einer punktförmigen Masse als Pendel ausgeht, muss bei dem physikalischen Pendel das Trägheitsmoment der Masse um den Schwerpunkt des Pendels berücksichtigt werden.
Physikalisches Pendel Bewegungsgleichung
Um die Bewegungsgleichungen des physikalischen Pendels aufzustellen benötigen wir die Eigenfrequenz  des Pendels. Sie lautet:
des Pendels. Sie lautet:
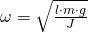
Die Bewegungsgleichungen lauten nun:
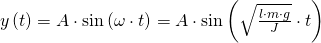
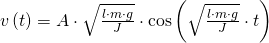
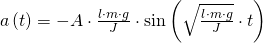
Durch Ableiten der Wegfunktion kann, auf die Geschwindigkeits- und die Beschleunigungsfunktion geschlossen werden.
Für den Winkel 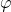 zum Zeitpunkt t gilt:
zum Zeitpunkt t gilt:
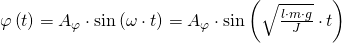
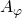 ist der Winkel von der Ruhelage zur maximalen Auslenkung des Pendels. Die Gleichung beschreibt die physikalische Lage des Pendels in Abhängigkeit von der Zeit t.
ist der Winkel von der Ruhelage zur maximalen Auslenkung des Pendels. Die Gleichung beschreibt die physikalische Lage des Pendels in Abhängigkeit von der Zeit t.
Stellt man den Drallsatz bezüglich des Aufhängepunktes auf, lässt sich die DGL ableiten:
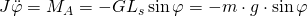

Schwingungsdauer und Frequenz Pendel
Weitere wichtige Größen sind die Schwingungsdauer T und die Schwingungsfrequenz f. Die Schwingungsdauer ist dabei wie folgt definiert:
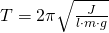
Die Schwingungsdauer gibt die benötigte Zeit für eine komplette Schwingung an. Der Kehrwert der Schwingungsdauer T entspricht der Schwingungsfrequenz f:
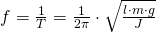
Trägheitsmoment Pendel
Ist das Trägheitsmoment des physikalischen Pendels in Bezug auf seinen Schwerpunkt bereits gegeben, kann das Trägheitsmoment im Bezug auf den Drehpunkt berechnet werden. Voraussetzung dafür ist, dass der Drehpunkt nicht auf dem Schwerpunkt liegt. Dazu wird der Satz von Steiner angewandt. Es gilt:
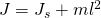
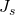 ist für viele geometrische Figuren in einem Tabellenwerk aufzufinden. Es kann allerdings auch experimentell bestimmt werden. Dazu wird folgende Formel angewandt.
ist für viele geometrische Figuren in einem Tabellenwerk aufzufinden. Es kann allerdings auch experimentell bestimmt werden. Dazu wird folgende Formel angewandt.
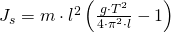
L entspricht dabei dem Abstand des Drehpunktes zum Schwerpunkt des Körpers. g ist die Fallbeschleunigung mit 9,81 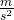 .
.
Reduzierte Pendellänge
Die Länge 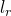 wird als reduzierte Pendellänge bezeichnet. Sie beschreibt die Länge, die der Länge l in der Schwingungsgleichung des mathematischen Pendels mit der gleichen Schwingungsdauer entspricht.
wird als reduzierte Pendellänge bezeichnet. Sie beschreibt die Länge, die der Länge l in der Schwingungsgleichung des mathematischen Pendels mit der gleichen Schwingungsdauer entspricht.
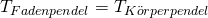
Es gilt:
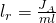
Da 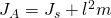 , kann die Formel auch so geschrieben werden:
, kann die Formel auch so geschrieben werden:
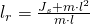
Mit Hilfe der Formel für den Trägheitsradius 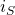 kann man diese Formel noch umformen.
kann man diese Formel noch umformen.
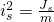
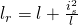
Außerdem wird so auch der Stoßmittelpunkt festgelegt. An diesem hat ein Stoß keine Lagerreaktion im Aufhängepunkt des Pendels zur Folge.
Kleine Ausschläge des Physikalischen Pendels
Haben wir sehr kleine Ausschläge des Pendels kann in der obigen Gleichung
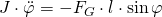
das  gleich
gleich 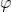 gesetzt werden. Dies gilt nur für sehr kleine Winkel
gesetzt werden. Dies gilt nur für sehr kleine Winkel  . Da wir hier kleine Ausschläge haben, rechnen wir mit der reduzierten Pendellänge
. Da wir hier kleine Ausschläge haben, rechnen wir mit der reduzierten Pendellänge 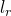
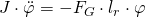
Über die Formel der Gewichtskraft kann die Gleichung weiter umgeformt werden.
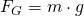
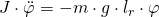
Nach Umstellung dieser Formel ist erkennbar, dass es sich um eine harmonische Schwingung handelt. Die Bewegungsgleichung lautet:
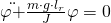
Das kann auch so geschrieben werden:
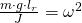
Die allgemeine Lösung dazu lautet:
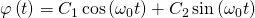
Damit erhält man folgende Formel für die Kreisfrequenz:
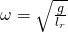
Die Frequenz der Schwingung entspricht:
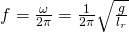
Die Schwingungsdauer kann wiederum über den Kehrwert der Frequenz ermittelt werden.
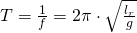
Außerdem kann das Massenträgheitsmoment durch einen Pendelversuch bestimmt werden. Dabei wird die Schwingungsdauer gemessen. Die reduzierte Pendellänge entspricht dabei:
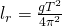
Damit folgt für das Massenträgheitsmoment 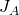 bezüglich des Aufhängepunktes:
bezüglich des Aufhängepunktes:
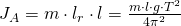
Außerdem gibt es noch das Massenträgheitsmoment bezüglich des Schwerpunktes 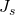 . Für dieses gilt:
. Für dieses gilt:
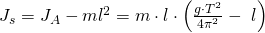
Große Ausschläge des Physikalischen Pendels
Bei großen Ausschlägen kann die Gleichung nicht linearisiert werden.
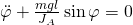
Die Lösung der DGL ist ein elliptisches Integral, dieses kann nicht in geschlossener Form integriert werden.
Allerdings muss die Summe aus kinetischer und potenzieller Energie bei der Pendelschwingung konstant sein.
Die Formel für die kinetische Energie des Pendels lautet:
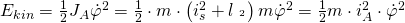
Für die potenzielle Energie gilt:
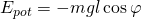
Die Summe beider werden nun zu 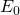 aufaddiert.
aufaddiert.
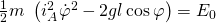
Je nachdem welche Anfangsenergie 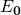 hat ergeben sich unterschiedliche Kurven. Nun können die Nullstellen gebildet werden.
hat ergeben sich unterschiedliche Kurven. Nun können die Nullstellen gebildet werden.
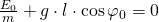
Dazu muss die obige Gleichung nach Null aufgelöst werden. Dabei muss beachtet werden, dass das Trägheitsmoment am Anfang gleich Null ist. Man erhält folgende Formel:
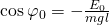
Da der Cosinus nur Werte zwischen -1 und 1 annehmen kann, können also nur Nullstellen für folgende Werte existieren:
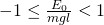
Aus der Gleichung kann geschlossen werden, dass für 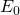 gleich –mgl, der Cosinus gleich eins sein muss. Für den zugehörigen Winkel
gleich –mgl, der Cosinus gleich eins sein muss. Für den zugehörigen Winkel 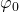 gilt:
gilt:
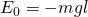
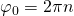
Dies entspricht dem Ruhezustand des Pendels. Bei der oberen instabilen Gleichgewichtslage ändert sich die Energie 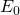 .
.
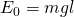
Hier wird der Cosinus minus eins. Für den Winkel 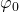 erhält man dann folgende Formel:
erhält man dann folgende Formel:
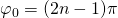
Für den Bereich 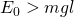 ist das physikalische Pendel am Rotieren.
ist das physikalische Pendel am Rotieren.