Video anzeigen

Reaktionen – Grundlagen

Du hast sicher schon mal Sprudelwasser selbst gemacht. Was das mit Reaktionen zu tun hat, erklären wir dir in diesem Beitrag.

Inhaltsübersicht

Einleitung

Bevor wir zu den Reaktionen kommen, wenden wir uns zunächst der Stoffbilanz zu. Grundsätzlich gilt, dass die gesamte Masse konstant bleiben muss, also keine Masse aus dem Nichts entstehen oder verschwinden kann. Für die Stoffmenge hingegen gilt das nicht, da sie nur die Anzahl der Moleküle beschreibt. Bei einer Reaktion kommen zwei oder mehr Stoffe zusammen und bilden daraus in der Regel neue Stoffe.

Bruttoreaktionsgleichung

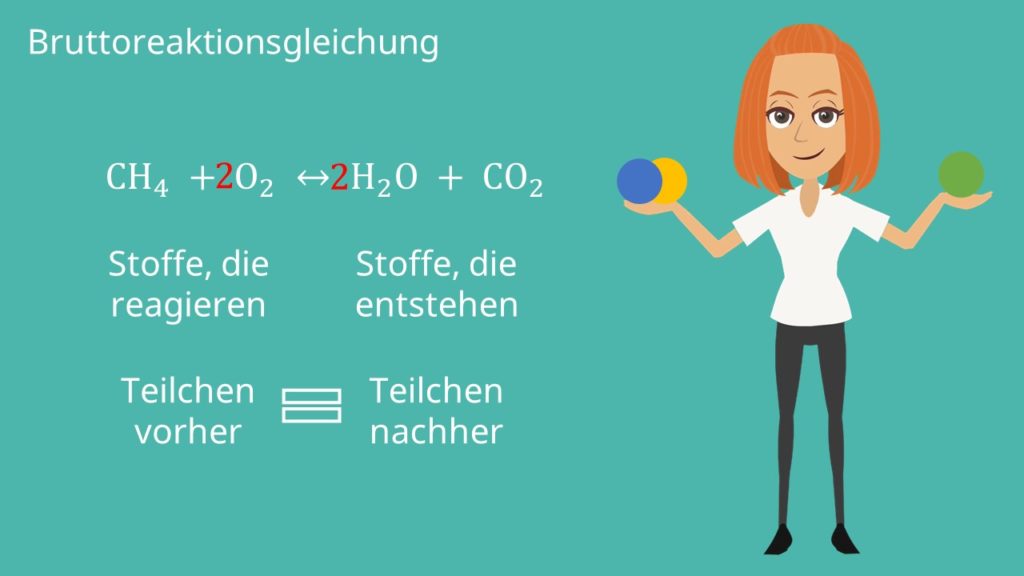
Das können wir in einer sogenannten Bruttoreaktionsgleichung betrachten. Hier stellen wir auf der linken Seite die Stoffe auf, die miteinander reagieren und rechts die Stoffe, die entstehen. Betrachten wir jetzt als Beispiel die Reaktion von Methan mit Sauerstoff. Dabei entstehen Wasser und 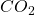CO_2 . Damit ergibt sich:

$CH_4+O_2\leftrightarrow H_2O+CO_2$

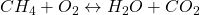
Das Problem ist, dass wir vor der Reaktion nicht die gleiche Teilchenanzahl haben wie nach der Reaktion. Beispielsweise werden aus 2 O, 3 O. Eines im Wasser und zwei im 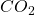CO_2 . Wir wollen nun ein Gleichgewicht der Teilchen erreichen. In unserem Fall brauchen wir dafür zweimal Sauerstoff und erhalten zweimal Wasser:

$CH_4+2O_2\leftrightarrow2H_2O+CO_2$

Bruttoreaktionsgleichung, Reaktionsgleichung, Chemisches Gleichgewicht, Chemisches Potential — Bruttoreaktionsgleichung

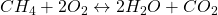
Umsatzvariable

Die Vorfaktoren kürzen wir jetzt mit \nu_i ab und die Anzahl, die im Index steht, mit „A i“.
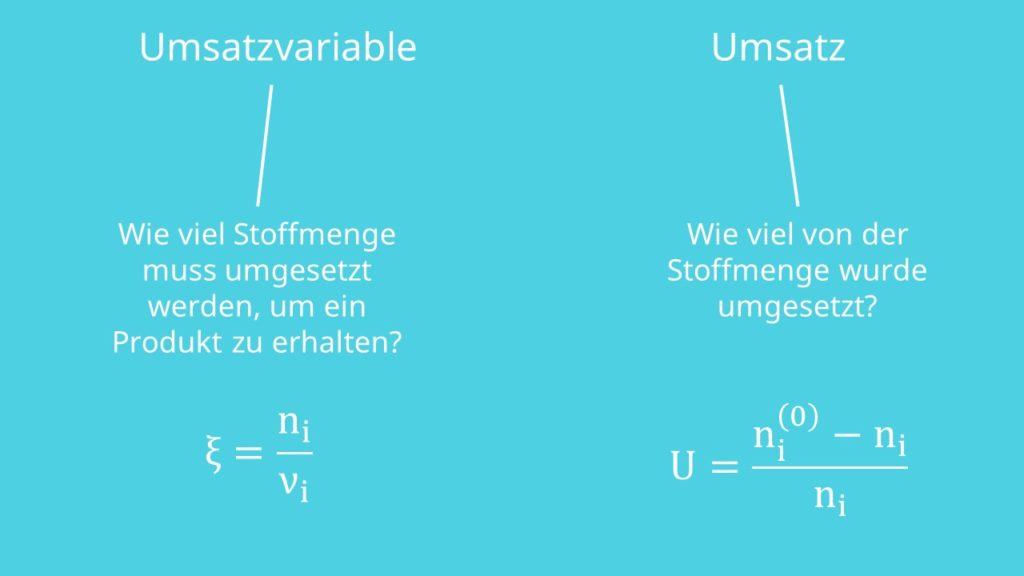
Wir definieren uns jetzt noch die Umsatzvariable und den Umsatz. Erstere beschreibt wie viel Stoffmenge umgesetzt werden muss, um ein Produkt zu erhalten. Dabei gibt es je Reaktion genau eine Umsatzvariable. Sie ist definiert als:

$\xi=\frac{n_i}{\nu_i}$

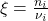
Das bedeutet, dass es für die Reaktion von Methan zu Wasser und 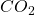CO_2 , nur eine einzige Umsatzvariable gibt.
Der Umsatz beschreibt, wie viel von der Stoffmenge umgesetzt wurde:

$U=\frac{n_i^{(0)}-n_i}{n_i}$

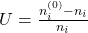
Edukte besitzen einen positiven und Produkte einen negativen Umsatz. Das liegt daran, dass der Umsatz eine Art des Verbrauchs ist und Produkte entstehen, also „negativ verbraucht“ werden.

Bruttoreaktionsgleichung, Reaktionsgleichung, Chemisches Gleichgewicht, Chemisches Potential — Umsatzvariable / Umsatz

Chemisches Gleichgewicht

Nachdem wir uns mit der Materie beschäftigt haben, kommen wir zum sogenannten chemischen Gleichgewicht. Ein Gleichgewicht kann sich nur einstellen, wenn zwei entgegengesetzte Reaktionen stattfinden. Das heißt, dass nicht nur Edukte zu Produkten reagieren, sondern auch Produkte teilweise zurück reagieren. Grundsätzlich gilt beim chemischen Gleichgewicht, dass die Änderung der freien Enthalpie gleich Null sein muss. Falls du dazu noch Fragen hast, dann schau dir am besten nochmal das Video zu thermodynamischen Potentialen an. Bei konstantem Druck und konstanter Temperatur erhalten wir:

$dG=\sum{\mu_i{dn}_i}=0$

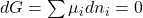
Mit Hilfe der Umsatzvariable ergibt sich:

$dG=\sum{\mu_i\nu_id\xi_}=0$

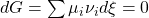
Ksi ist für die Gleichung nicht weiter relevant, da wir Stoffeigenschaften und keine Reaktionseigenschaften betrachten wollen. Stellen wir den Term nun um, erhalten wir.

$\frac{dG}{d\xi}=\sum{\mu_i\nu_i}=0$

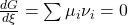
Chemisches Potential

Das chemische Potential Müh i definiert sich dabei als:

$\mu_i=\mu_{0i}+RT\ln\funcapply(a_i)$

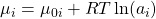
Wir erhalten neben dem Term für den Reinstoff noch einen Mischungsterm. „A i“ beschreibt die Zusammensetzung des Gemisches und ist davon abhängig, ob wir eine ideale Flüssigkeit oder ein ideales Gas betrachten:

Setzen wir das chemische Potential in die Summe ein und formen ein wenig um, erhalten wir:

$e^{-\sum{\nu_i\frac{\mu_{0i}}{RT}}}=\prod{a_i}^{\nu_i}$

Bruttoreaktionsgleichung, Reaktionsgleichung, Chemisches Gleichgewicht, Chemisches Potential — Chemisches Potential

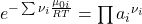
Gleichgewichtskonstante

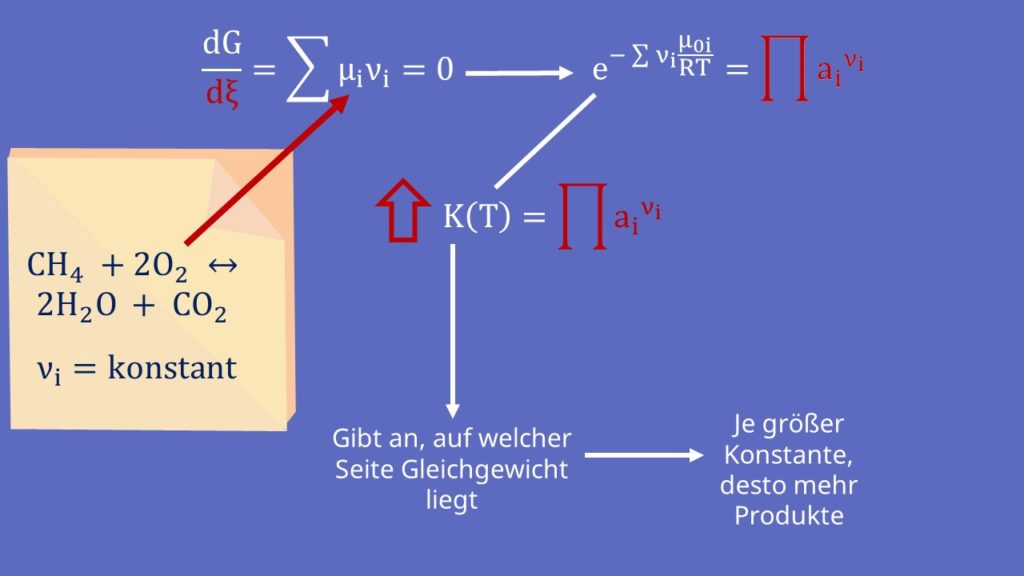
Der Term mit der e-Funktion ist die sogenannte Gleichgewichtskonstante K. Sie gibt an, auf welcher Seite das Gleichgewicht liegt. Betrachten wir wieder die Reaktion von vorhin. Die Nüh i kennen wir. Sie sind konstant. Damit ergibt sich:

$K\left(T\right)=\prod{a_i}^{\nu_i}=\frac{{a_{H_2O}}^2{a_{CO_2}}^1}{{a_{CH_4}}^1{a_{O_2}}^2}$

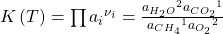
Erhöhen wir jetzt die Gleichgewichtskonstante, muss sich auch die rechte Seite erhöhen. Das geht aber nur, wenn die Terme über dem Bruchstrich, also der Anteil der Produkte, größer werden. Das heißt bei größerer Gleichgewichtskonstante erhalten wir mehr Produkte.
Jetzt kennen wir die rechte Seite der Gleichung. Wie erhöhen wir jetzt aber die Gleichgewichtskonstante? Dafür betrachten wir diese genauer: Der Wert bestimmt sich über den Exponenten:

$-\sum{\nu_i\frac{\mu_{0i}}{RT}}$

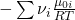
Die Nüh i sind wieder konstant. Also schauen wir uns jetzt „Müh Null i“ an. Wir wissen, dass das chemische Potential immer größer gleich Null ist und wir es durch Änderung der Temperatur beeinflussen können. Das heißt, dass die entscheidende Größe, um die Reaktionskonstante zu beeinflussen, die Temperatur ist.

Beispiel

Bei der Reaktion von 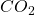CO_2 mit Wasser zu Kohlensäure beispielsweise, steht die Kohlensäure auf der Produktseite. Erhöhen wir die Temperatur, sinkt die Gleichgewichtskonstante und das Gleichgewicht verschiebt sich entsprechend auf die Eduktseite. Die Kohlensäure reagiert also zurück. Du kennst das Phänomen bestimmt, wenn du im Sommer dein Getränk zu lange in der Sonne lässt. Die Kohlensäure verschwindet und das Getränk schmeckt nicht mehr.
So jetzt weißt du, wie du verhindern kannst, dass die Kohlensäure zu schnell aus dem Wasser verschwindet.

Beliebte Inhalte aus dem Bereich Thermodynamik

Reaktionen - Grundlagen

Verbrennung - Übung

Hallo, leider nutzt du einen AdBlocker.

Auf Studyflix bieten wir dir kostenlos hochwertige Bildung an. Dies können wir nur durch die Unterstützung unserer Werbepartner tun.

Schalte bitte deinen Adblocker für Studyflix aus oder füge uns zu deinen Ausnahmen hinzu. Das tut dir nicht weh und hilft uns weiter.

Danke!
Dein Studyflix-Team

Wenn du nicht weißt, wie du deinen Adblocker deaktivierst oder Studyflix zu den Ausnahmen hinzufügst, findest du hier eine kurze Anleitung. Bitte .