Reaktionsenthalpie und Reaktionsentropie
Du hast sicher schon mal an einem Lagerfeuer gesessen. Dabei findet eine Reaktion statt. Wie du diese energetisch beschreiben kannst, zeigen wir dir jetzt.
Inhaltsübersicht
Einleitung
Wir haben bereits die Größen für das chemische Gleichgewicht kennengelernt. Uns fehlt jetzt aber noch die energetische Betrachtung. Das Problem ist, dass wir bei Reaktionen nicht mit der gleichen Stoffmengenzusammensetzung austreten, mit der wir eingetreten sind. Denn die Stoffe reagieren. Wir wollen jetzt herausfinden, ob die Reaktion Energie benötigt, also endotherm ist, oder ob sie Energie freisetzt, also exotherm ist.
Dafür definieren wir uns zu Beginn Standardwerte für die Temperatur und den Druck. Die Temperatur T0 ist 25 Grad Celsius und der Druck p0 beträgt genau ein bar.
Im Reaktor stellen wir uns jetzt drei Schritte vor:
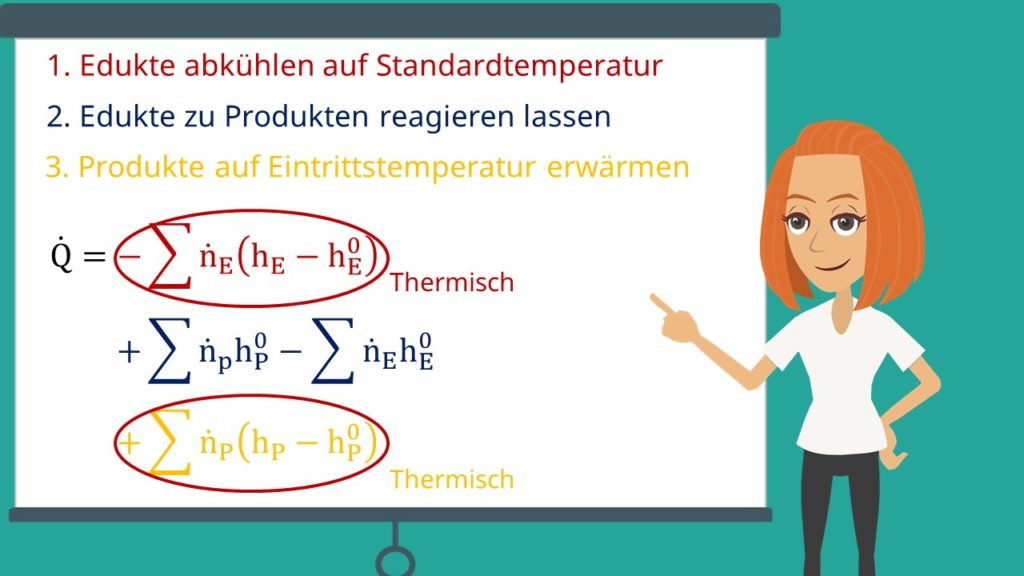
1. Edukte abkühlen auf Standardtemperatur
2. Edukte zu Produkten reagieren lassen und
3. Produkte wieder auf Eintrittstemperatur erwärmen
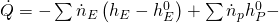
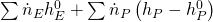
Aus den Schritten eins und drei erhalten wir die thermischen Anteile. Die Reaktion ist unser chemischer Anteil. Dieser kann geschrieben werden als:
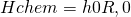
Delta h Null R Null ist die Reaktionsenthalpie. Diese kann entweder bei der Reaktion entstehen, oder sie wird benötigt, um die Reaktion zu starten.
Wenn wir jetzt unter Standardbedingungen in den Reaktor eintreten, müssen wir die thermischen Anteile nicht betrachten. Das liegt daran, dass „h e“ durch das Abkühlen „h e null“ entspricht und „h p“ durch das Erwärmen „h p null“. Die beiden Terme lassen sich also streichen und wir erhalten:
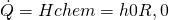
Ist die Reaktionsenthalpie also negativ, liegt ein negativer Wärmestrom vor. Er verlässt unser System und unsere Reaktion wird somit exotherm. Andersherum haben wir bei einer positiven Reaktionsenthalpie einen eintretenden Wärmestrom und daher eine endotherme Reaktion.
Standardbildungsenthalpie
Jetzt können wir uns unter Standardbedingungen noch weitere Größen definieren. Es gibt die Standardbildungsenthalpie, die die Enthalpie eines Stoffes unter Standardbedingungen beschreibt.
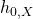
Das X im Index ist hier einfach ein Platzhalter für den jeweiligen Stoff. Die Standardbildungsenthalpie ist für jeden Stoff in der Literatur zu finden.
Reaktionsentropie
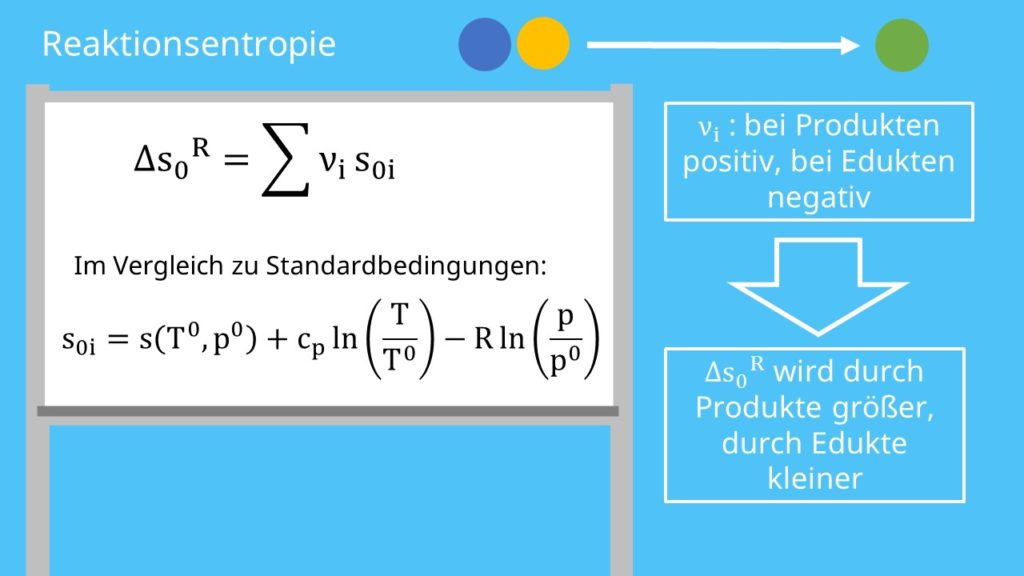
Als nächstes betrachten wir die Reaktionsentropie. Diese bestimmen wir ähnlich zur Enthalpie und definieren sie als:
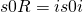
„S null i“ ist die jeweilige Entropie der Reinstoffe. Zur Erinnerung: Nüh ist bei Produkten immer positiv und bei Edukten negativ. Praktisch gesehen heißt das, dass wir durch die Produkte Entropie hinzugewinnen, durch die Edukte hingegen verlieren. Wenn wir uns das überlegen ist das auch logisch, da die Edukte „verschwinden“ und die Produkte „erscheinen“.
Nun ist „s Null i“ nicht unter Standardbedingungen definiert. Deshalb bestimmen wir diese Entropie, indem wir die Änderungen im Vergleich zu den Standardbedingungen verwenden:
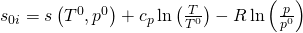
Damit können wir die Entropie bei Reaktionen bestimmen.
Kommen wir jetzt zur freien Enthalpie. Du erinnerst dich bestimmt an die Formel dazu. Wir wollen diese wieder bei Standardwerten und für Reinstoffe betrachten:
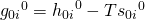
Die Null im Exponenten heißt, dass wir bei Standardbedingungen sind. Damit können wir uns wieder die freie Reaktionsenthalpie bestimmen. Setzen wir die Formel für die freie Enthalpie bei Reinstoffen ein, ergibt sich:
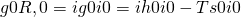
Betrachten wir die Summe nun etwas genauer. Zuerst trennen wir den hinteren Term auf. Du erkennst sicher, dass wir jetzt genau die Standardbildungsenthalpie beziehungsweise -entropie betrachten. Damit ergibt sich:
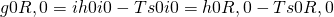
Jetzt kannst du ganz einfach feststellen, ob das Lagerfeuer exotherm oder endotherm ist: Du spürst die Wärme, die das Lagerfeuer ausstrahlt. Damit ist die Reaktion exotherm. So kannst du direkt erkennen, dass die Reaktionsenthalpie kleiner Null sein muss. Mit der Wärmeabgabe kannst du so also die Reaktionsenthalpie des Feuers bestimmen. Viel Spaß und bis bald!