Scherung
Du möchtest wissen was eine Scherung in der Mechanik ist und wie du sie berechnen kannst? Perfekt, denn genau das erklären wir dir in diesem Artikel.
Inhaltsübersicht
Scherung, Grundlagen und Einheit
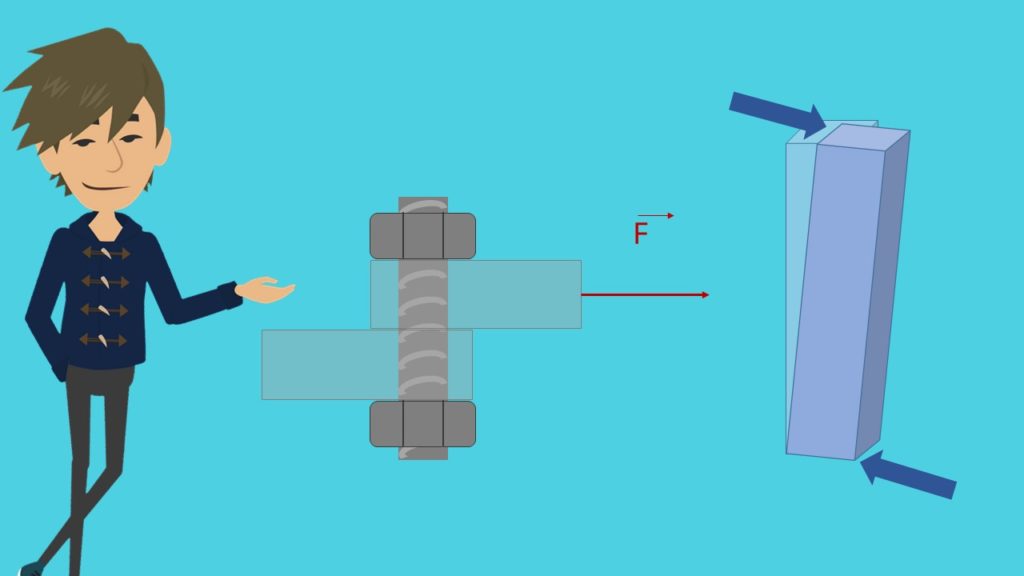
Unter Scherung oder auch Gleitung versteht man die Belastung eines Körpers durch entgegengesetzte parallele Kräfte.
Dabei wirken die scherenden Kräfte tangential zur Materialoberfläche. Durch die sogenannte Scherbelastung kann das Material verbogen, verschoben oder verdreht werden. Ein typisches Bauteil, auf das oftmals Scherkräfte einwirken sind Bolzen oder Nieten.
Das Symbol für die Scherkraft ist der griechische Buchstabe tau und die Messeinheit beträgt Pascal. Für eine elastische Scherung gilt folgende Formel:
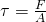
Scherung für verschiedene Materialien berechnen
Eine Erweiterung der Formel beinhaltet das Schubmodul G.
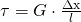
Es wird auch als Schermodul, Gleitmodul, oder Torsionsmodul bezeichnet. Das Schubmodul G ist eine Materialkonstante, das heißt für bestimmte Materialien ist G immer gleich. Es beschreibt den Proportionalitätsfaktor der relativen Längenänderung des Materials. Je größer das G, desto größer ist die Steifigkeit des Materials.
Scherspannungen führen generell schneller zu Brüchen als Zug- oder Druckspannungen.
Berechnung des Scherwinkels
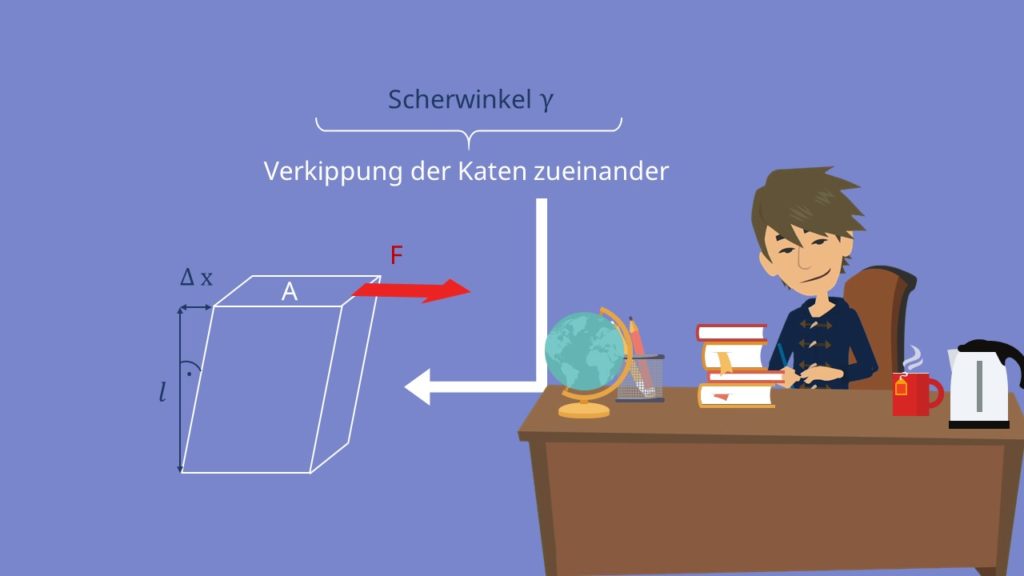
Ein weiteres wichtiges Maß ist der Scherwinkel 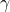 . Der Scherwinkel beschreibt die Verkippung der Kanten zueinander. Dies entsteht durch die Verformung des Körpers.
. Der Scherwinkel beschreibt die Verkippung der Kanten zueinander. Dies entsteht durch die Verformung des Körpers.
Es gilt:
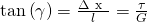
Die Scherung entspricht dem Tangens des Scherwinkels, beziehungsweise der Verschiebung der Fläche um Delta x im Verhältnis zur Höhe des Körpers l. Eine weitere Möglichkeit dies zu berechnen ist die Schubspannung durch das Gleitmodul G zu teilen. Ist 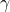 sehr klein, also die Verformung nicht allzu groß, entspricht
sehr klein, also die Verformung nicht allzu groß, entspricht 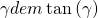 und die Gleichung kann folgendermaßen umgestellt werden.
und die Gleichung kann folgendermaßen umgestellt werden.
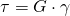
Dies gilt gemäß dem Hooke´schen Gesetz. Wenn du darüber mehr erfahren möchtest, kannst du dir unser Video dazu ansehen.
Sehr schön! Nun kennst du die Scherung und bist mit den wichtigsten Formeln für die Berechnung ausgestattet!