Schubmittelpunkt berechnen
Du möchtest wissen, was der Schubmittelpunkt ist und wie du ihn berechnen kannst? Hier zeigen wir dir das Ganze an einem einfachen Beispiel.
Inhaltsübersicht
Was ist der Schubmittelpunkt? – Verschiedene Profile
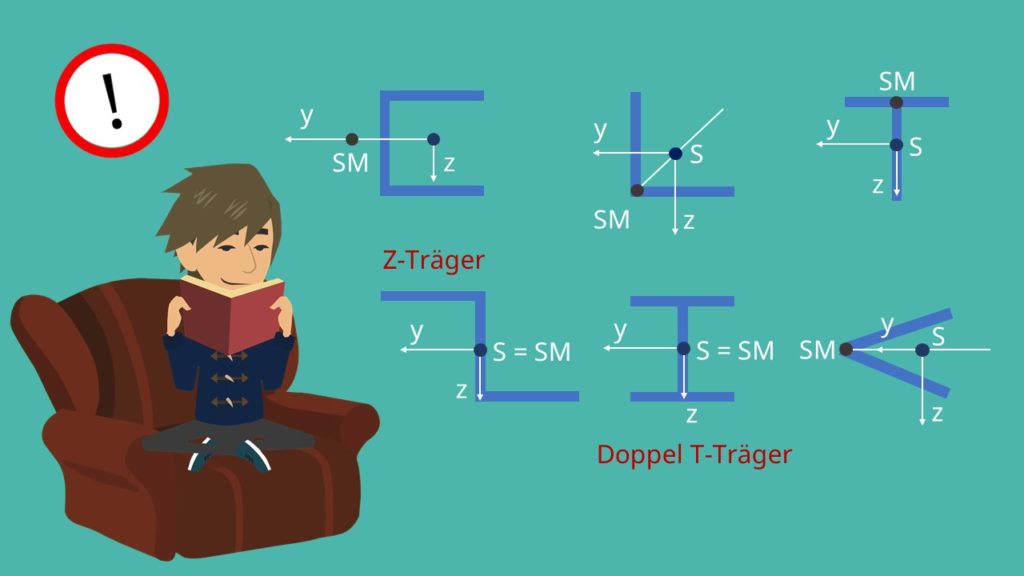
Der Schubmittelpunkt wird auch als Querkraftmittelpunkt oder Drillruhepunkt bezeichnet. Er beschreibt denjenigen Punkt eines Profilquerschnittes, an dem die Resultierende der Querkräfte, also der seitlich wirkenden Kräfte angreift, ohne eine Verdrillung bzw. eine Torsion zu verursachen. Einsatzbereiche des Schubmittelpunktes sind zum Beispiel in der Statik oder Tragwerksplanung. Hier sehen wir beispielhaft einige Schubmittelpunkte bei verschiedenen Profilen.
Es gibt bei den Schubmittelpunkten einige Sonderfälle. Bei doppelsymmetrischen oder punktsymmetrischen Profilen entspricht der Schubmittelpunkt dem geometrischen Schwerpunkt S. Dies ist zum Beispiel bei dem Doppel T-Träger oder dem Z-Träger der Fall.
Bei einfachsymmetrischen oder unsymmetrischen Profilen sind der Schwerpunkt und der Schubmittelpunkt allerdings unterschiedlich. Bei den einfach-symmetrisch Profilen befindet sich der Schubmittelpunkt immer auf der Symmetrieachse. Querschnittprofilen, die aus mehreren geradlinigen Teilen zusammengesetzt werden, haben den Schubmittelpunkt auf dem Schnittpunkt der einzelnen Profilmittellinien.
Die Formel für die Berechnung des Schubmittelpunktes bei einfachen symmetrischen dünnwandigen Profilen lautet:
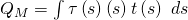
Schubmittelpunkt C Profil
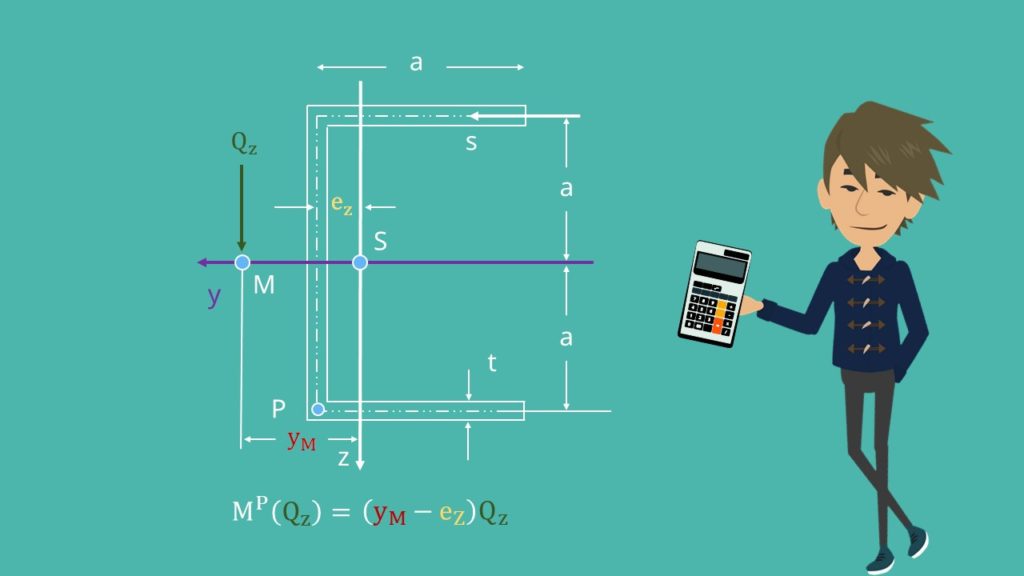
Sehen wir uns das ganze doch einmal am Beispiel des C-Profils an.
Dies ist einfach-symmetrisch an der Y-Achse. Somit muss sich der Schubmittelpunkt auf der Spiegelachse befinden. Das bedeutet, dass das Moment der Querkraft 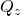 bezüglich des Punktes P mit dem des Schubflusses übereinstimmen muss. Berechnen wir zunächst das Moment der Querkraft.
bezüglich des Punktes P mit dem des Schubflusses übereinstimmen muss. Berechnen wir zunächst das Moment der Querkraft.
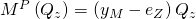
Dazu multiplizieren wir die Querkraft mit dem Abstand zum Mittelpunkt M. Dieser berechnet sich aus dem Abstand zum Schwerpunkt abzüglich des Schwerpunktabstands. Dieser berechnet sich wie folgt:
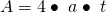
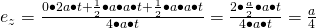
Schubmittelpunkt berechnen
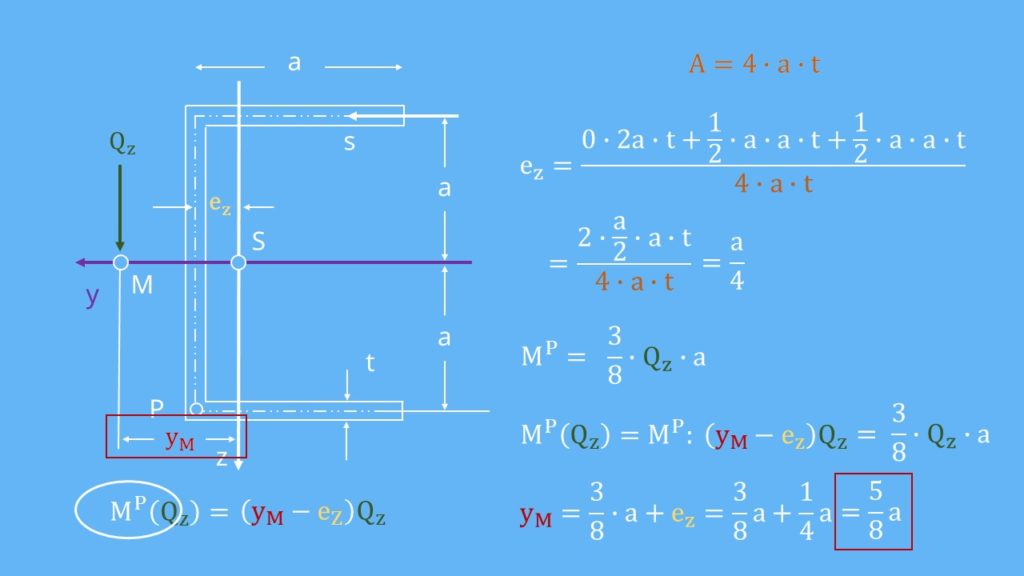
Die Fläche A des Profils beträgt 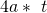 . Dies setzen wir in die Formel für den Schwerpunkt ein. Da der mittlere Balken schon auf dem Schwerpunkt liegt zählen wir nur die Schwerpunkte des oberen und des unteren Balkens zusammen. Wir erhalten für den Abstand
. Dies setzen wir in die Formel für den Schwerpunkt ein. Da der mittlere Balken schon auf dem Schwerpunkt liegt zählen wir nur die Schwerpunkte des oberen und des unteren Balkens zusammen. Wir erhalten für den Abstand 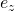 in x-Richtung den Wert
in x-Richtung den Wert 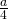 .
.
Nun fehlt uns noch das Moment von P. Dieser ist uns mit folgendem Wert gegeben:
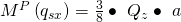
Wir erhalten für das M also 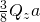 . Nun setzen wir die Momente gleich und lösen nach
. Nun setzen wir die Momente gleich und lösen nach 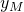 auf.
auf.
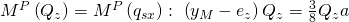
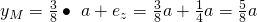
Wir erhalten 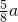 für den Abstand
für den Abstand 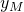 .
.
Nun weißt du, was der Schubmittelpunkt ist und wie du ihn für dünnwandige Profile berechnen kannst.