Schubspannung
In diesem Beitrag gehen wir auf die Definition der Schubspannung und deren Formel ein. Ebenfalls schauen wir uns eine Beispielrechnung an.
Du möchtest das alles lieber in einem Video erklärt bekommen, anstatt langen Text zu lesen? Dann schau doch hier mal rein.
Inhaltsübersicht
Schubspannung einfach erklärt
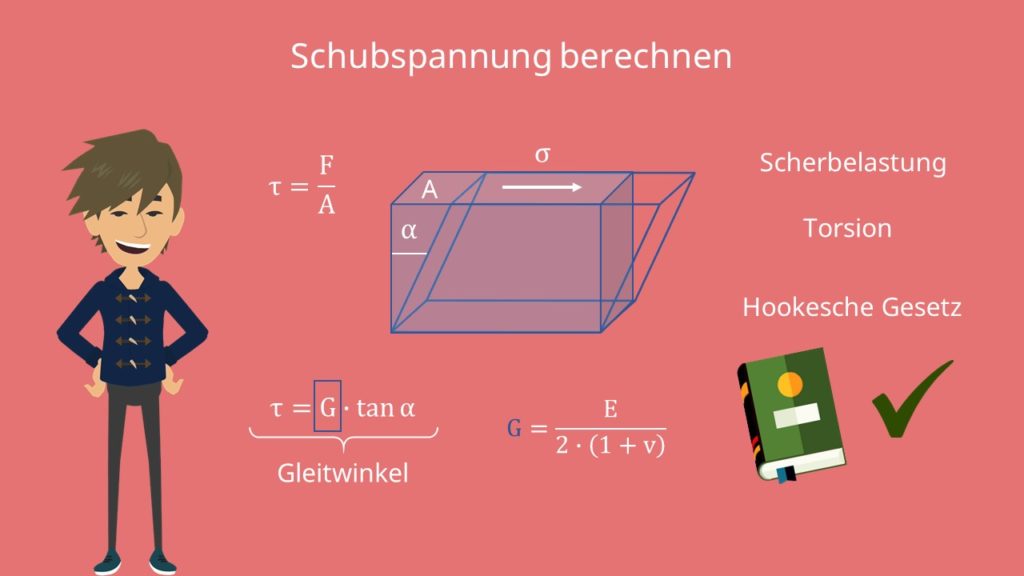
Belastest du einen Körper, beispielsweise durch eine Kraft von Außen, so erzeugst du eine mechanische Spannung in diesem. Die Spannung kann je nach Angriffsrichtung in eine Normalspannung und eine Schubspannung aufgeteilt werden. Bei der Normalspannung greift eine Kraft senkrecht zu einer Oberfläche an. Hingegen wirkt bei der Schubspannung eine Kraft tangential an der Oberfläche des Körpers. Die auf diese Art angreifende Kraft führt zu einer Scherung des Körpers. Aufgrunddessen wird die Schubspannung auch als Scherspannung oder Tangentialspannung bezeichnet.
Schubspannung Formel
Die Schubspannung ist definiert durch eine Kraft F, die tangential an einer Oberfläche A eines Körpers angreift. Somit gilt vereinfacht die Formel:
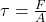
Die genaue Herleitung diser Spannung findest du in diesem Beitrag .
Wenn die Verdrehung oder Längenänderung des Körpers proportional zu der angreifenden Kraft verläuft, so gilt das Hookesche Gesetz für die Schubspannung und du kannst es in der Formel mit berücksichtigen.
Durch eine tangential anliegende Kraft F verdreht sich unser Körper um einen Winkel 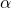 . Der Tangens des Winkels ist proportional zu der anliegenden Spannung, weshalb gilt:
. Der Tangens des Winkels ist proportional zu der anliegenden Spannung, weshalb gilt:
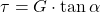
G ist dabei das Schubmodul. Der Winkel 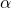 kann auch als Gleitwinkel bezeichnet werden. Außerdem gilt für kleine Winkel ungefähr:
kann auch als Gleitwinkel bezeichnet werden. Außerdem gilt für kleine Winkel ungefähr:
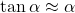
Hier lässt sich dann die Formel vereinfachen zu:
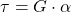
Außerdem kannst du das Schub- oder auch Schermodul G ganz einfach aus der Poissonzahl  und dem Elastizitätsmodul E des Werkstoffes berechnen. Die Formel dafür lautet:
und dem Elastizitätsmodul E des Werkstoffes berechnen. Die Formel dafür lautet:
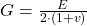
Schubspannung Einheit
Die Schubspannung setzt sich aus der Kraft F pro Flächeneinheit A zusammen und ähnelt damit stark der Definition des Druckes. Eine Kraft wird generell immer in Newton [N] angegeben, wobei die Fläche in Meter zum Quadrat [m2] berechnet werden kann.
Teilst du Newton durch m2 so erhältst du die Einheit Pascal [Pa]. Pascal ist damit nicht nur die Einheit des Druckes, sondern auch die der Schub- oder Scherspannung.
Schubspannungen berechnen
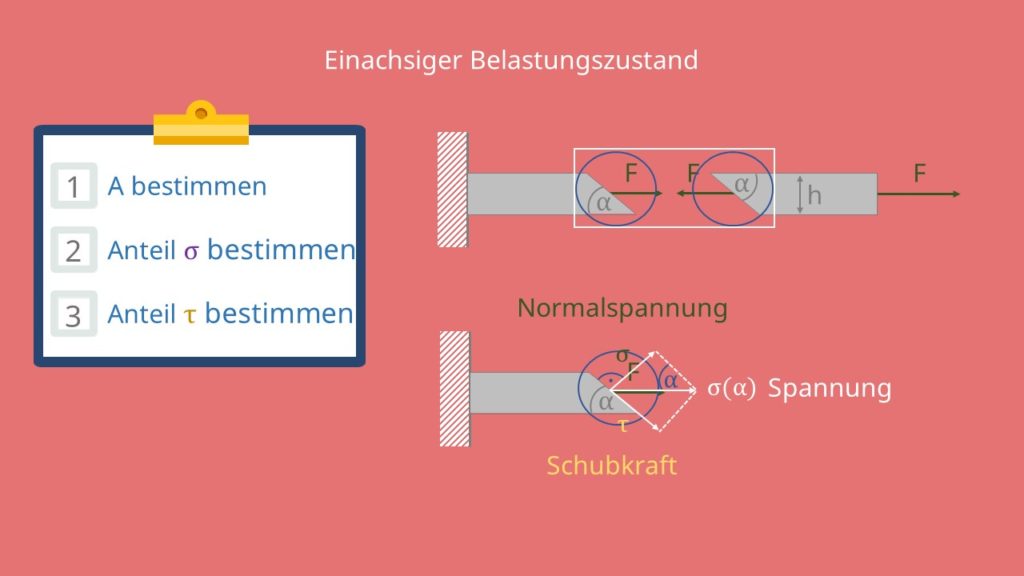
Sehen wir uns einen einachsigen Belastungszustand an, wie er in der Mechanik häufig vorkommt. Wir haben hier einen Stab, der geschnitten wurde. Ähnlich wie in der Statik zeichnen wir die Zugkraft F an mehreren Stellen ein, da sie auch an der Schnittstelle im Gleichgewicht sein muss. Es bleibt allerdings immer dieselbe Kraft. Wie du hier sehen kannst wirkt diese auf eine schräge Fläche.
Betrachten wir einmal nur die Schnittfläche. Da die Spannung 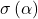 schief zur Fläche steht, müssen wir sie in die Normalspannung
schief zur Fläche steht, müssen wir sie in die Normalspannung 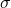 , die senkrecht zur Fläche steht und die tangentiale Schubkraft
, die senkrecht zur Fläche steht und die tangentiale Schubkraft 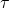 aufteilen.
aufteilen.
Nun müssen wir zunächst die Fläche A, auf die die Kraft F wirkt, bestimmen und dann den Anteil der Normal- und der Schubspannung an der gesamten wirkenden Spannung 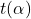 herausfinden. Für die A betrachten wir nun zuerst den abgeschnittenen Teil des Balkens genau.
herausfinden. Für die A betrachten wir nun zuerst den abgeschnittenen Teil des Balkens genau.
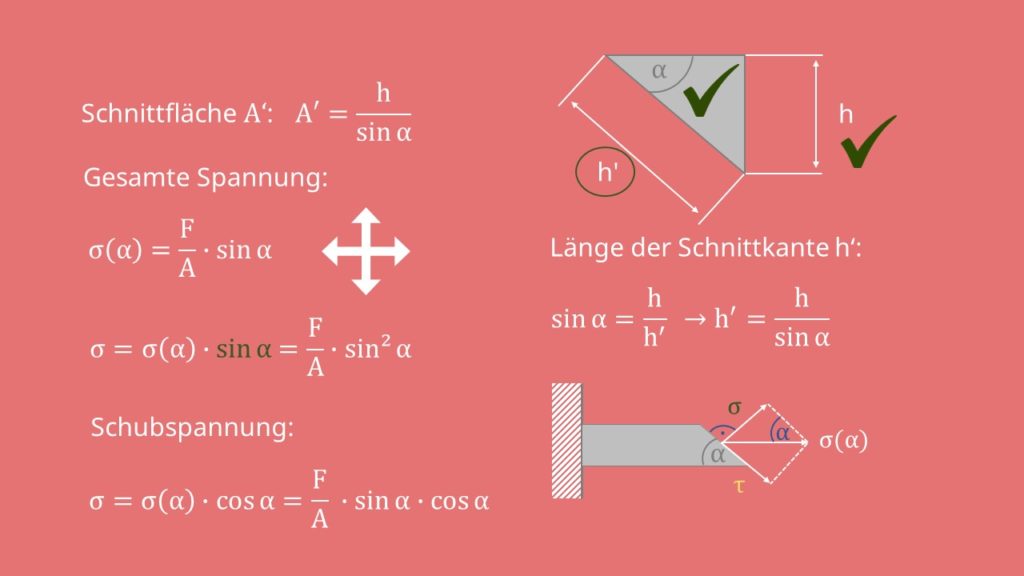
Haben wir den Winkel 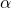 und die Höhe h gegeben können wir die Länge h´ der Schnittkante bestimmen. Die Länge bleibt gleich. Daher können wir, um A´ zu berechnen, auch die frontale Fläche des Balkens durch den Sinus von
und die Höhe h gegeben können wir die Länge h´ der Schnittkante bestimmen. Die Länge bleibt gleich. Daher können wir, um A´ zu berechnen, auch die frontale Fläche des Balkens durch den Sinus von 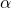 teilen. Es ergibt sich für die gesamte Spannung die Gleichung:
teilen. Es ergibt sich für die gesamte Spannung die Gleichung:
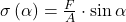
Nun müssen wir diese aufteilen. Auch hier können wir wieder den Winkel 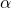 zu Rate ziehen. Wir betrachten noch einmal die vorherige Grafik. Für die Normalspannung können wir den Sinus einsetzen. Es ergibt sich folgende Gleichung:
zu Rate ziehen. Wir betrachten noch einmal die vorherige Grafik. Für die Normalspannung können wir den Sinus einsetzen. Es ergibt sich folgende Gleichung:
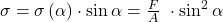
Wir setzen unser Ergebnis von vorhin ein und erhalten diese Gleichung. Dasselbe mache wir nun für die Schubspannung. Hier setzen wir den Cosinus ein und erhalten:
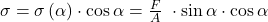
Das ist die Schubspannung, die unter Einwirkung einer Zugkraft auf eine scheife Fläche wirkt. Falls du die Spannung für eine Querkraft berechnen willst, kannst du hier reinschauen.
Maximale Schubspannung
Die maximale Normalspannung ergibt sich dabei bei einem Winkel von 90°, da hier A am kleinsten ist. Hier ist die Schubspannung gleich 0. Du kannst auch noch berechnen, unter welchen Schnittwinkel die Spannung am größten ist.
Dazu leitest du 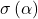 nach
nach 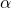 ab und setzt diese gleich null. Es ergibt sich das Maximum der Schubspannung:
ab und setzt diese gleich null. Es ergibt sich das Maximum der Schubspannung:
![Rendered by QuickLaTeX.com \frac{\sigma\left(\alpha\right)}{\alpha}=\frac{F}{A}\ \left[\cos{\alpha}\cdot\cos{\alpha}+\sin{\left\{\alpha\cdot\left(-\sin{\alpha}\right\}\right)}\right]=\frac{F}{A}\cdot\left(\cos^2{\alpha}-\sin^2{\alpha}\right)=0](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-67ef4a5a664292d3825ea988d8a82260_l3.png)
Damit dies zutrifft muss also 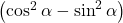 null ergeben, da F und A praktisch nie null werden. Das heißt beide Größen müssen gleich groß sein.
null ergeben, da F und A praktisch nie null werden. Das heißt beide Größen müssen gleich groß sein.
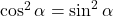
Dies trifft nur für den Winkel 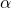 ist gleich 45° zu. Also ist die Schubspannung bei 45° maximal.
ist gleich 45° zu. Also ist die Schubspannung bei 45° maximal.