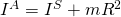Schwingungslehre III – Partikuläre Lösung
Du willst wissen wie du Schwingungen mit der partikulären Lösung beschreiben kannst? Dann bist du hier genau richtig!
Inhaltsübersicht
Mathematische Beschreibung von Schwingungen
Am Anfang gehen wir noch einmal die Grundlagen durch: Wir erhalten Schwingungsgleichungen in der Regel in Form von Differentialgleichungen. Diese können in homogene und inhomogene Gleichungen unterschieden werden. Im letzten Video hat sich alles um die homogenen Gleichungen gedreht. Jetzt schauen wir uns die inhomogenen – oder auch partikulären – Gleichungen genauer an:
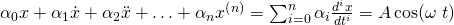
Beispiel
Diese Differentialgleichung lösen wir, indem wir die homogene Lösung und die partikuläre Lösung addieren.
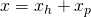
Die partikuläre Lösung kann man mit Hilfe des Ansatzes:
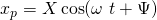
bestimmen.
Nachdem wir die Grundlagen zur Lösung von inhomogenen Differentialgleichungen nochmal durchgegangen sind, wollen wir diese auf ein Beispiel anwenden. Dazu nehmen wir das gleiche Beispiel wie im Video zu den homogenen Gleichungen, damit du die beiden gut miteinander vergleichen kannst. Betrachten wir also eine Rolle mit der Masse m gleich 10kg, dem Radius R gleich 30 cm und einem Massenträgheitsmoment im Schwerpunkts 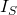 von 0,45 kg
von 0,45 kg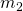 : Diese Kugel ist im Schwerpunkt mit einem Feder-Dämpfer-System verbunden. Das heißt, wir haben Feder und Dämpfer parallelgeschaltet und dann mit der Rolle verbunden. Die Federkonstante k ist gleich 15 Newton pro Meter und die Dämpfungskonstante d 30 Ns pro m.
: Diese Kugel ist im Schwerpunkt mit einem Feder-Dämpfer-System verbunden. Das heißt, wir haben Feder und Dämpfer parallelgeschaltet und dann mit der Rolle verbunden. Die Federkonstante k ist gleich 15 Newton pro Meter und die Dämpfungskonstante d 30 Ns pro m.
Nun unterliegt das System zusätzlich noch einer Wegerregung. Diese greift in der Regel immer an der Feder an und sorgt für eine weitere Auslenkung. Das heißt, die Erreger bewegt sich hin und her und spannt bzw. entspannt die Feder zusätzlich. Diese Bewegung wird beschrieben durch:
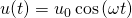
Die Werte u0 und Omega sind bereits bekannt. Dabei ist u0 die Amplitude des Erregers mit 20 cm und Omega die Kreisfrequenz des Erregers mit 3 Rad pro Sekunde. Die Bewegung des Erregers startet in positive x-Richtung. Da wir wissen, dass wir eine Rollbewegung betrachten, nutzen wir zur Beschreibung eben dieser Bewegung erstmal den Winkel phi.
DGL aufstellen und Drallsatz bilden
Jetzt weißt du wie das System aussieht. Nun wollen wir als erstes die Differentialgleichung bezüglich x aufstellen und anschließend die Lösung dazu bestimmen.
Dafür bilden wir den Drallsatz bezüglich des Berührpunktes A von Rolle und Boden. Den Drallsatz bezüglich des Schwerpunkts anzuwenden, ist hier nicht sinnvoll, da dort die Dämpfer- bzw. Federkraft angreifen.
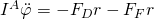
Die Dämpferkraft ergibt sich aus der Rollgeschwindigkeit und der Dämpfungskonstante und die Federkraft aus dem zurückgelegten Weg und der Federkonstante. Bei der Federkraft müssen wir jetzt zusätzlich noch die Wegerregung betrachten. Diese bewirkt, dadurch, dass sie zu Beginn in positive x-Richtung geht, eine Verringerung des Weges und somit auch der Spannung bzw. der Kraft. Wir erhalten damit:
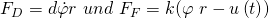
Nun müssen wir nur noch das Massenträgheitsmoment bezüglich A bestimmen: