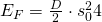Schwingungsgleichung Federpendel
Dieser Artikel behandelt die Schwingungsgleichung von einem Federpendel. Dabei stellen wir die Schwingungsgleichung auf und beschreiben wichtige Variablen und Eigenschaften der Gleichung. Des Weiteren rechnen wir ein Beispiel, lösen die allgemeine Differentialgleichung für Schwingungen und gehen auf die wirkenden Energien bei dem Federpendel ein.
In unserem Video dazu, erklären wir dir das alles in wenigen Minuten. Auf was wartest du noch? Schau doch einfach mal rein!
Inhaltsübersicht
Federpendel Definition
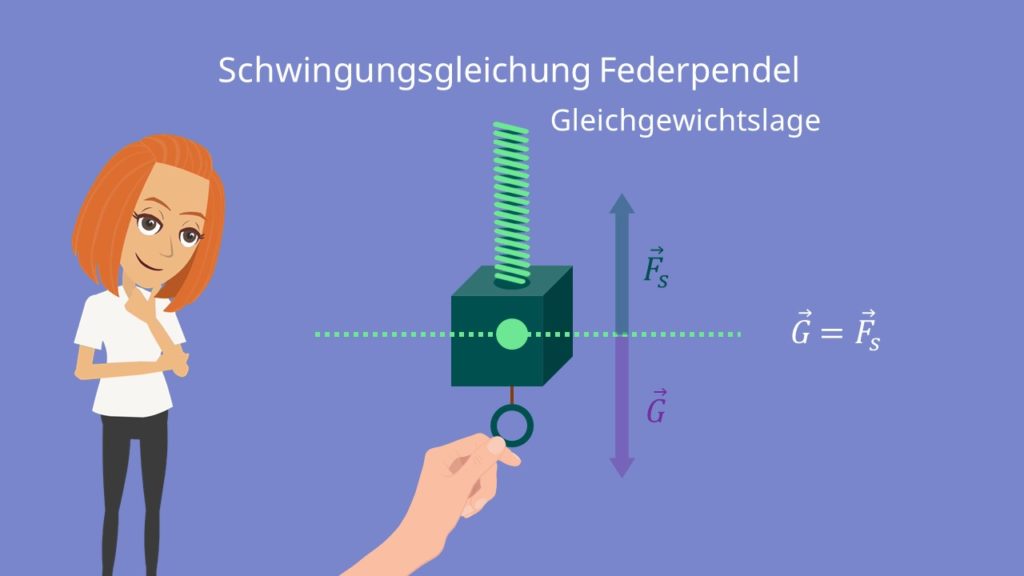
Das Federpendel wird auch als Federschwinger bezeichnet und kann als eine harmonische Schwingung aufgefasst werden. Dabei besteht das Pendel aus einer Schraubenfeder und einer daran befestigten Masse. Die dazugehörige Ruhelage wird durch das Zusammenspiel von der Schwer- und Federkraft bestimmt. Mathematisch kann die Bewegung des Pendels mit einer Schwingungsgleichung beschrieben werden.
Beschleunigung
Wird der Körper nach unten gezogen, erhöht sich die Federkraft 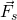 . Da die Gewichtskraft jedoch gleichbleibt, beschleunigt die Feder den Körper nach oben. Die Kraft nimmt ab, bis die Gleichgewichtslage wieder erreicht wird. Da die Geschwindigkeit des Pendelkörpers aufgrund des Trägheitsprinzips zur Ruhelage konstant zunimmt und dort am höchsten ist, schwingt das Pendel darüber hinaus.
. Da die Gewichtskraft jedoch gleichbleibt, beschleunigt die Feder den Körper nach oben. Die Kraft nimmt ab, bis die Gleichgewichtslage wieder erreicht wird. Da die Geschwindigkeit des Pendelkörpers aufgrund des Trägheitsprinzips zur Ruhelage konstant zunimmt und dort am höchsten ist, schwingt das Pendel darüber hinaus.
Nun ist die Gewichtskraft  größer als die Federkraft und der Körper wird zuerst gebremst und dann ab dem Umkehrpunkt wieder zurückgetrieben. Der Bewegungsvorgang wiederholt sich nun.
größer als die Federkraft und der Körper wird zuerst gebremst und dann ab dem Umkehrpunkt wieder zurückgetrieben. Der Bewegungsvorgang wiederholt sich nun.
Die rücktreibende Kraft entspricht der Federkraft der Schraubenfeder:
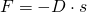
D ist die materialabhängige Federkonstante der Feder und s die Auslenkung der Feder vom Ruhezustand. Die Berechnung der Konstante haben wir in einem eigenen Artikel behandelt. Nun können wir mit dem Newtonschen Grundgesetz den Zusammenhang zwischen Spannkraft und Beschleunigung herstellen.

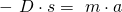
Die Größen a und s sind also proportional zueinander. Falls bei einer Dämpfung keine Energie entzogen wird, wiederholt sich die erste Schwingung periodisch immer wieder.
Das Federpendel kann auch von außen angeregt werden. Dann wird die Amplitude der Schwingung immer größer und es kann zu einer Resonanzkatastrophe kommen.
Schwingungsgleichung des Federpendels aufstellen
Um die Differentialgleichung der Schwingung aufzustellen setzen wir die Weg-Zeit Gleichung für die Beschleunigung in die vorherige Formel ein und lösen auf. In dem Artikel zur harmonischen Schwingung findest du die genaue Weg-Zeit Gleichung.
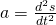
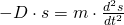
Nun haben wir eine Differentialgleichung zweiter Ordnung.
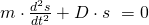
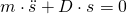
Umgestellt nach 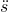 ergibt sich:
ergibt sich:
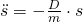
Diese Gleichung beschreibt die Bewegung des Federpendels. Jetzt wird eine Funktion gesucht, die zweimal abgeleitet wieder die Ursprungsfunktion plus die Konstante 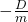 ergibt. Dafür müssen wir auf die Anfangsbedingungen des Pendels zurückgreifen. Zum Zeitpunkt
ergibt. Dafür müssen wir auf die Anfangsbedingungen des Pendels zurückgreifen. Zum Zeitpunkt 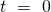 ist die Pendelmasse auf die Position
ist die Pendelmasse auf die Position 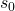 ausgelenkt. Das bedeutet für die erste Bedingung:
ausgelenkt. Das bedeutet für die erste Bedingung:
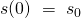
Für die zweite Anfangsbeziehung gilt, dass die Geschwindigkeit zu dem Zeitpunkt t=0 auch null sein muss, da wir uns am Punkt der Auslenkung in Ruhe befinden.
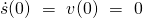
Nun wird eine Funktion gesucht, die diese Anfangsbedingungen und die Differentialgleichung erfüllt. Ein Ansatz wäre die folgende Gleichung:
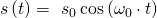
Die Größe 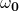 muss zunächst definiert werden. Dafür wird die zweite Ableitung der Cosinunsfunktion verwendet:
muss zunächst definiert werden. Dafür wird die zweite Ableitung der Cosinunsfunktion verwendet:
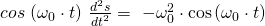
Daraus kann ableitet werden, dass 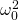 gleich unserem Vorfaktor
gleich unserem Vorfaktor 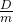 sein muss.
sein muss.
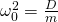
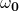 wird daher auch als die ungedämpfte Eigenkreisfrequenz bezeichnet und kann in die Differentialgleichung eingesetzt werden. Somit gilt es folgenden Zusammenhang zu lösen:
wird daher auch als die ungedämpfte Eigenkreisfrequenz bezeichnet und kann in die Differentialgleichung eingesetzt werden. Somit gilt es folgenden Zusammenhang zu lösen:
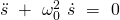
Eigenkreis- und Schwingungsfrequenz des Federpendels
Die Eigenkreisfrequenz gibt an, welche Winkelgeschwindigkeit ein Punkt haben muss, damit seine Frequenz mit dem des Pendelkörpers übereinstimmt.
Die allgemeine Formel für diese lautet:

Für die ungedämpfte Eigenkreisfrequenz eines Federpendels gilt, wie aus der DGL abgeleitet:
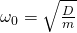
Sie ist umso größer, je größer die Federkonstante D ist und je kleiner seine Masse m ist.
Ungedämpft bedeutet, dass keine Reibungen auftreten und die Amplitude
konstant ist.
Schwingungsdauer Federpendel
Die Schwingungsdauer des Federpendels kann aus der allgemeinen Formel der Kreisfrequenz abgeleitet werden.
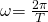
Wir setzten diese in die ungedämpfte Eigenfrequenz (1) ein und lösen die Gleichung nach T (2) auf
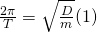
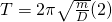
Die Formel drückt die benötigte Zeit für eine Schwingung aus.
Auch hier kannst du dein Wissen wieder mit dem Artikel Schwingungsdauer und Amplitude vertiefen.
Schwingungsgleichung des Federpendels lösen
Für das Lösen der Schwingungsgleichung benutzen wir eine Exponentialfunktion:

Die zweite Ableitung der Funktion lautet:

Wir setzen das Ganze in unsere Schwingungsgleichung ein (1) und erhalten (2):

Durch Umformung ergibt sich:
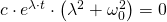
Da c als Konstante nicht null werden kann und die e-Funktion nie null sein kann, muss der in Klammern gesetzte Teil der Formel gleich Null sein.
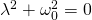
Das bedeutet:
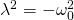
Für die Lösung erhalten wir somit:
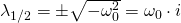
Das bedeutet, in diesem Fall haben wir zwei komplexe Lösungen.
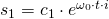
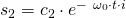
Die Lösungsgleichung lautet:
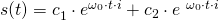
Nun müssen wir noch die Konstanten 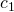 und
und 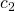 bestimmen. Der Oszillator erreicht nach einem Viertel seiner Schwingungsdauer die maximale Auslenkung
bestimmen. Der Oszillator erreicht nach einem Viertel seiner Schwingungsdauer die maximale Auslenkung 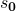 . Es gilt
. Es gilt
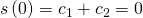
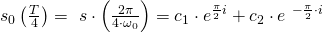
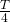 entspricht bei einer Periodenlänge von
entspricht bei einer Periodenlänge von 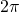 genau
genau 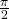 . Nun schreiben wir die Formel von einer Exponentialform mit der Hilfe des Eulerschen Formel in eine Sinus- /Cosinus Funktion um.
. Nun schreiben wir die Formel von einer Exponentialform mit der Hilfe des Eulerschen Formel in eine Sinus- /Cosinus Funktion um.
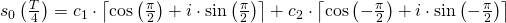
Nach entsprechendem Einsetzen der Sinus und Cosinus Werte haben wir:
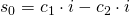
Aus der Bedingung im Ruhezustand, wissen wir, dass 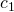 minus
minus 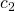 ist.
ist.
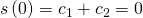
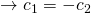
Oben eingesetzt, kann folgende Gleichung aufgestellt werden:
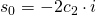
Für unsere Konstanten können wir also nun folgende Formel berechnen:
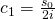
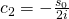
Dies setzen wir nun in unsere Lösungsformel ein.
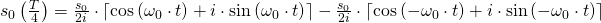
Umgeformt erhalten wir damit durch die Beachtung der Quadrantenregeln (1) (2), folgende Lösungen:
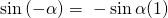
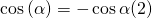
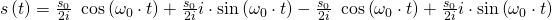
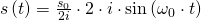
Jetzt kann auch die imaginäre Zahl i aus der Gleichung gekürzt werden und die Lösung der Differentialgleichung ist:

Das ist die Beschreibung des Weges für das ideale Federpendel.
Federpendel Beispiel
Wir können über die Schwingungsgleichung auch die Geschwindigkeit und die Beschleunigung des Federpendels berechnen.
Dazu muss die Schwingungsgleichung zweimal abgeleitet werden.
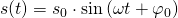
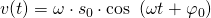
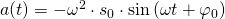
Somit ist die Geschwindigkeitsfunktion um 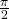 nach links verschoben und die Beschleunigungsfunktion um
nach links verschoben und die Beschleunigungsfunktion um 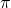 nach links.
nach links.
Energie des Federpendels
Die Energie eines Federpendels setzt sich aus der kinetischen und der potentiellen Energie zusammen.
Für die Berechnung der kinetischen Energie gilt:
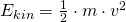
Für die Geschwindigkeit  setzen wir
setzen wir 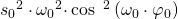 ein.
ein.
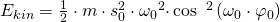
Mit der Formel für die Eigenkreisfrequenz kann dies noch vereinfacht werden:
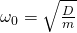
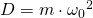
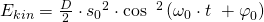
Nun benötigen wir noch die potenzielle Energie.
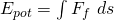
Diese kann als das Integral der Federkraft über die Zeit beschrieben werden. Setzen wir die Formel für die Federkraft ein, erhalten wir.
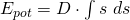
Wir lösen nun das Integral auf.
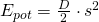
Nun haben wir sowohl die potenzielle als auch die kinetische Energie und müssen dies nur noch aufaddieren.
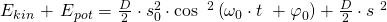
Die potenzielle Energie ist maximal bei maximaler Auslenkung. Nun können wir s durch die Bewegungsgleichung s(t) des Federpendels ersetzen.
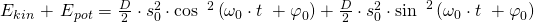
Laut den trigonometrischen Regeln gilt:
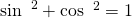
Also erhalten wir für die Energie der Feder 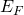 letztendlich:
letztendlich: