Spannungstensor und Spannungszustände
Du willst wissen wieso eine Feder immer wieder in ihren ursprünglichen Zustand zurück kehrt? Das erklären wir dir in diesem Beitrag
Inhaltsübersicht
Normal- und Schubspannungen
In der Festigkeitslehre allgemein betrachten wir – wie in der Statik – die Systeme, die im statischen Gleichgewicht stehen. Wir können also keine Bewegung beobachten. Falls du dazu noch Fragen hast, schau du dir doch nochmal das Video zur Gleichgewichtsbedingung der Statik an. Zusätzlich dazu wollen wir jetzt noch die Verformung von Körper betrachten. Diese ist oft ein wesentliches Kriterium zur Bauteilauslegung. Schließlich willst du ja nicht, dass das Fahrrad, dass du gerade benutzt, zerbricht. Die Größen, die dafür betrachtet werden, sind die Spannung und die Dehnung. Wir beschäftigen uns jetzt mit dem Begriff der Spannung.
Schnittkräfte und Spannungsvektoren
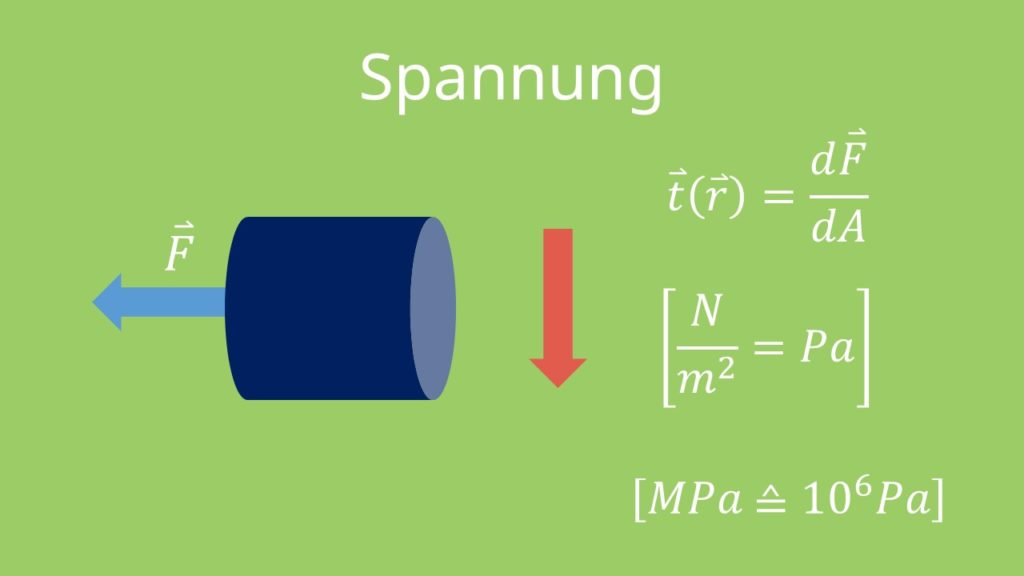
Dazu betrachten wir einfach einen beliebigen Körper, der von Kräften belastet ist, sich aber im Gleichgewicht befindet. Diesen Körper schneiden wir nun an einer beliebigen Stelle. An dieser Stelle erhalten wir dann eine Schnittkraft. Daraus ergibt sich dann der sogenannte Spannungsvektor. Der Spannungsvektor, zeigt in die gleiche Richtung, in die auch die Schnittkraft zeigt. Er ist definiert als:
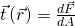
Die Einheit dieses Vektors ist Newton pro Quadratmeter bzw. Pascal. In der Regel liegt die Spannung in der Größenordnung von Megapascal. Das entspricht Zehn hoch 6 Pascal.
Der gefundene Vektor ist nun abhängig von der Kraft, der Fläche und ihrer Orientierung. Er betrachtet erst einmal nur eine bestimmte Richtung, die vom Schnitt abhängig ist. Um das Problem zu lösen, betrachten wir ein infinitesimal kleines Volumenelement mit orthogonalen Flächen. Das heißt wir betrachten einen ganz kleinen Würfel, bei dem je zwei Flächen in x, y und z-Richtung orientiert sind. Die Orientierung ist gegeben durch den sogenannten Normalenvektor 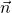 , der aus der Fläche heraus zeigt. Die Normalenvektoren, die in Koordinatenrichtung zeigen, nehmen wir hier als positiv an.
, der aus der Fläche heraus zeigt. Die Normalenvektoren, die in Koordinatenrichtung zeigen, nehmen wir hier als positiv an.
Zu jeder Fläche können wir nun einen Spannungsvektor bestimmen, der allerdings nicht senkrecht zur Fläche stehen muss. Dabei betrachten wir nur die Flächen mit positiven Normalenvektoren. Wir erhalten also die drei Vektoren 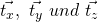 . Jeder dieser Vektor hat wieder Komponenten in x, y und z-Richtung. Diese wollen wir jetzt in einer Matrix zusammenstellen, um die Spannungen für das gesamte Volumenelement zu beschreiben. Diese Matrix wird Spannungstensor Sigma genannt.
. Jeder dieser Vektor hat wieder Komponenten in x, y und z-Richtung. Diese wollen wir jetzt in einer Matrix zusammenstellen, um die Spannungen für das gesamte Volumenelement zu beschreiben. Diese Matrix wird Spannungstensor Sigma genannt.
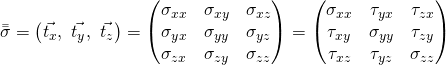
Spannungstensor lesen
Die Indizierung der einzelnen Komponenten folgt dabei einem einfachen Schema: Der erste Index steht für die Richtung der einzelnen Komponente. Der zweite Index steht für die Richtung des Normalenvektors. Das heißt wir übernehmen hier den Index des Vektors. Betrachten wir also 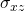 , dann beschreibt dieser Wert die Spannung der x-Komponente zur Fläche, die in z-Richtung zeigt. Weiterhin unterscheiden wir dabei in Normalspannungen Sigma und Schubspannungen Tau. Normalspannungen sind die Spannungen, die auch in Richtung der Fläche gehen, alle anderen sind Schubspannungen. Du erkennst also, dass die Normalspannung auf der Hauptdiagonalen liegen.
, dann beschreibt dieser Wert die Spannung der x-Komponente zur Fläche, die in z-Richtung zeigt. Weiterhin unterscheiden wir dabei in Normalspannungen Sigma und Schubspannungen Tau. Normalspannungen sind die Spannungen, die auch in Richtung der Fläche gehen, alle anderen sind Schubspannungen. Du erkennst also, dass die Normalspannung auf der Hauptdiagonalen liegen.
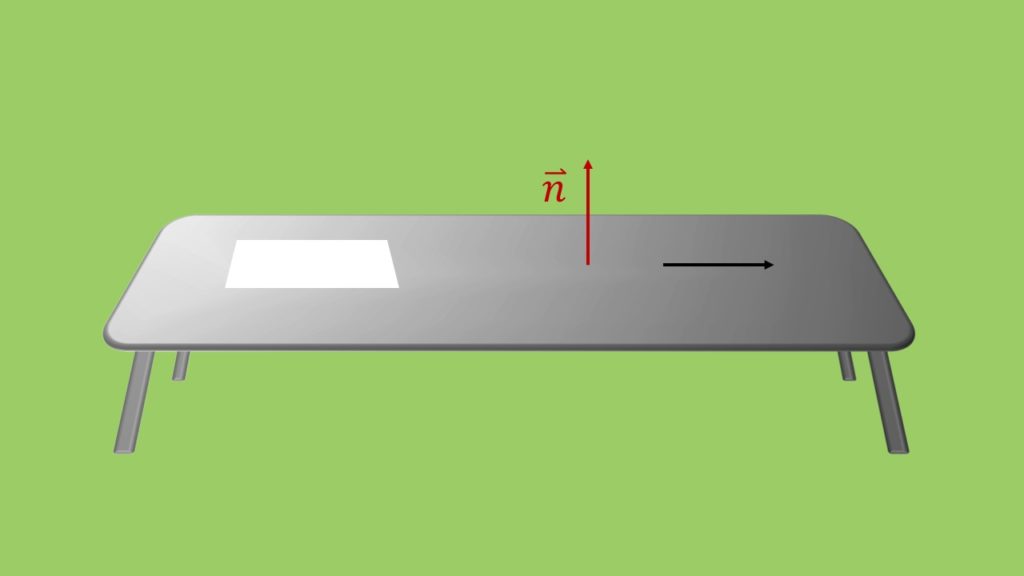
Damit du dir das besser vorstellen kannst, stellen wir uns jetzt ein Blatt auf deinem Tisch vor, das wir verschieben: der Normalenvektor der Fläche zeigt jetzt nach oben, die Bewegung ist aber nicht in diese Richtung.
Ähnlich kannst du dir Schubspannungen vorstellen. Die Matrix selbst ist symmetrisch. Doch was heißt das? Wir können die Matrix an der Hauptdiagonalen spiegeln und erhalten die gleichen Werte. Daraus folgt für uns, dass zum Beispiel 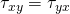 ist. Das gilt auch für die übrigen Komponenten.
ist. Das gilt auch für die übrigen Komponenten.
Aus der Matrix können wir auch wieder einen Spannungsvektor für eine bestimme Fläche eines beliebigen Elements bestimmen. Dafür multiplizieren wir den Spannungstensor einfach mit dem Normalenvektor der Fläche, also:
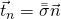
Jetzt können wir die Spannung eines Elements beschreiben und wenden uns im nächsten Schritt den möglichen Spannungszuständen zu. Wir unterscheiden hier in drei verschiedene Zustände:
- Einachsig
- Eben
- Räumlich
Der einachsige Spannungszustand ist der einfachste Fall. Wir betrachten den ebenen Fall und belasten einen Körper nur in x- oder y-Richtung. Zur Veranschaulichung betrachten wir einen Balken, der „lang gezogen“ wird. Diesen können wir nun unter verschiedenen Winkeln schneiden und erhalten je nach Winkel verschiedene Spannungsvektoren.
Diesen Vektor können wir dann wieder in Normal- und Schubspannungen aufteilen.