Stabilitätskriterium nach Nyquist I
Du sitzt vor dem Kapitel „Systemeigenschaften“ und könntest bei dem Begriff Nyquist-Kriterium direkt an die Decke gehen? Tief durchatmen, wir verschaffen dir Abhilfe!
Inhaltsübersicht
Das Stabilitätskriterium nach Nyquist über die Dauerschwingung
Im Gegensatz zum Hurwitz-Kriterium , kannst du mit dem Nyquist-Kriterium auch Regelkreise hinsichtlich ihrer Stabilität beurteilen, die Totzeitglieder beinhalten.
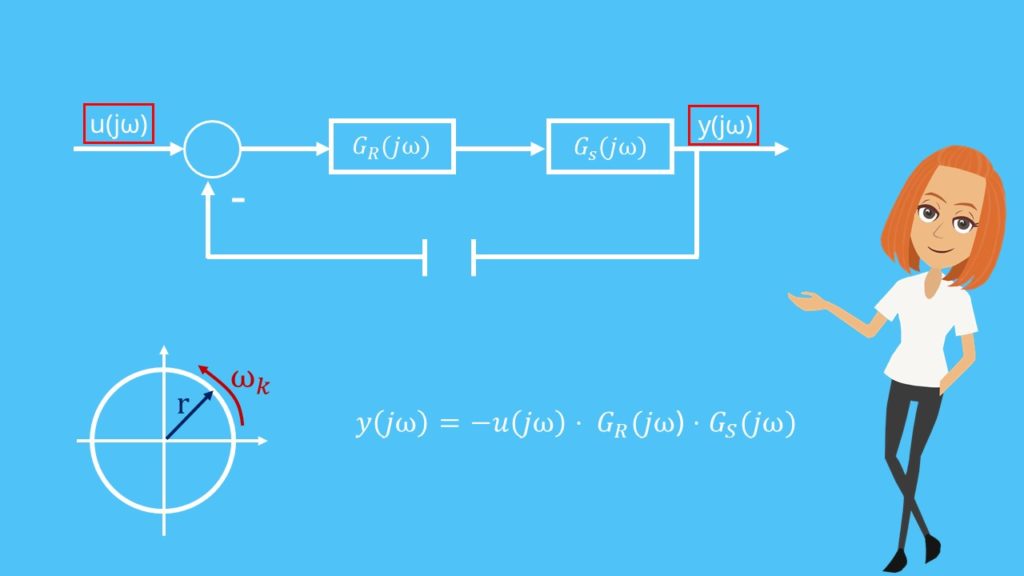
Ein rückgekoppeltes System nennt man auch geschlossenen Regelkreis oder geschlossene Kette. Wäre der Rückführungspfeil nicht vorhanden, spricht man vom offenen Regelkreis oder der offenen Kette. In ihr darf eine Totzeit vorkommen. Wir werden jetzt anhand der offenen Kette eine Aussage über die geschlossene Kette treffen. Dazu betrachten wir ein Blockschaltbild, in dem die Rückkopplung unterbrochen ist: Es muss für diesen Regelkreis eine Bedingung geben, unter der er Dauerschwingungen mit einer bestimmten Kreisfrequenz 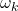 ausführt.
ausführt.
Zwischen den harmonischen, also sinusförmigen, Ein- und Ausgangsgrößen, lässt sich eine Beziehung formulieren:
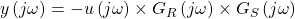
Frequenzgang und Dauerschwingung
Daraus kannst du jetzt den Frequenzgang des offenen Kreises 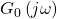 ableiten.
ableiten.
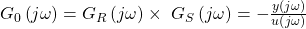
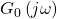 entspricht dabei dem Produkt aus
entspricht dabei dem Produkt aus 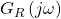 und
und 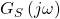 .
.
Ist erfüllt, dass diese Beziehung – 1 entspricht,
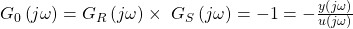
so wird die geschlossene Kette eine ungedämpfte Schwingung mit der Kreisfrequenz 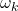 durchführen. An diesem Punkt sagt man, dass sich das System an seiner Stabilitätsgrenze befindet. Da durch die Rückkopplung eine Vorzeichenumkehr stattfindet und wir ein Minus erhalten, gibt es zwischen den beiden Schwingungen des Ein- und Ausgangs erst einmal eine Phasenverschiebung um -180 Grad.
durchführen. An diesem Punkt sagt man, dass sich das System an seiner Stabilitätsgrenze befindet. Da durch die Rückkopplung eine Vorzeichenumkehr stattfindet und wir ein Minus erhalten, gibt es zwischen den beiden Schwingungen des Ein- und Ausgangs erst einmal eine Phasenverschiebung um -180 Grad.
Eine Dauerschwingung gibt es allerdings erst bei einer Phasenverschiebung um -360 Grad. Diese fehlenden -180 Grad müssen also noch durch den Frequenzgang der Kette 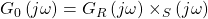 aufgebracht werden. Als weitere besondere Bedingung für eine Dauerschwingung muss die Verstärkung, die die Kette bewirkt, bei der Frequenz
aufgebracht werden. Als weitere besondere Bedingung für eine Dauerschwingung muss die Verstärkung, die die Kette bewirkt, bei der Frequenz 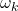 genau 1 betragen. Diese Verstärkung nennt man Kreisverstärkung
genau 1 betragen. Diese Verstärkung nennt man Kreisverstärkung 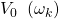 . Sie entspricht also dem Betrag des Frequenzgangs für
. Sie entspricht also dem Betrag des Frequenzgangs für 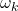 .
.
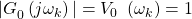
Bedingungen für die offene Kette
Das heißt, dass die Schwingung konstant bleibt und die Ein- und Ausgangsamplituden 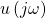 und
und 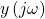 genau gleich groß sind. Somit kannst du dir aus diesen Überlegungen zwei wichtige Bedingungen für die offene Kette merken:
genau gleich groß sind. Somit kannst du dir aus diesen Überlegungen zwei wichtige Bedingungen für die offene Kette merken:
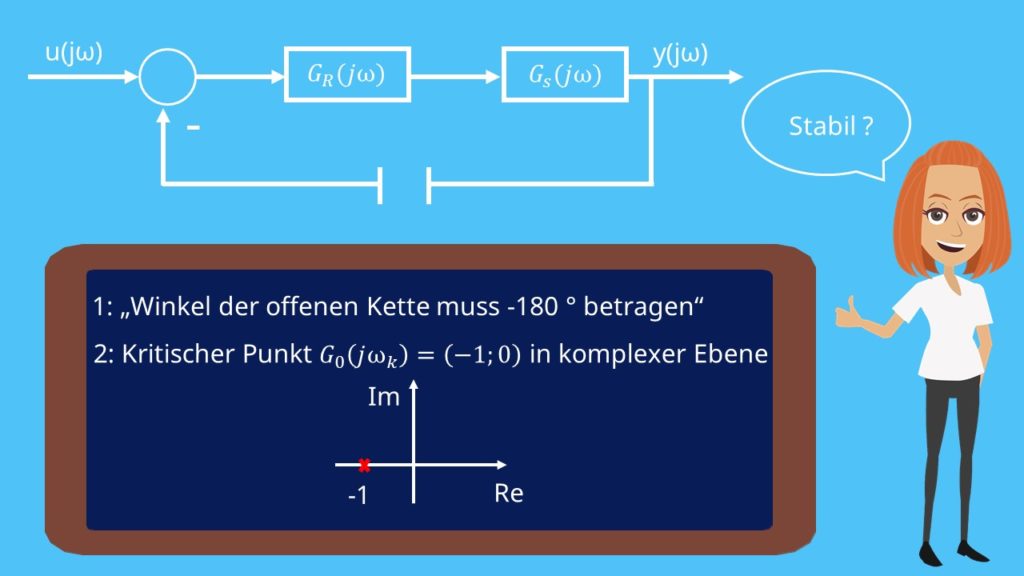
Erstens: Der Winkel der offenen Kette muss -180 Grad betragen
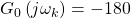
Und zweitens: Es gibt einen sogenannten kritischen Punkt 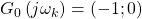 in der komplexen Ebene, der ganz entscheidend dafür ist, ob ein System als stabil beurteilt wird.
in der komplexen Ebene, der ganz entscheidend dafür ist, ob ein System als stabil beurteilt wird.
Was du mit diesem kritischen Punkt machst und was das Nyquist-Kriterium mit der sogenannten Ortskurve am Hut hat, erklären wir dir in unserem nächsten Video.