Statischer Festigkeitsnachweis
Du bist gerade dabei, deinen neuen Kleiderschrank einzurichten, hast aber Bedenken, dass die Kleiderstange das Gewicht deiner vielen Klamotten nicht aushält? In den nächsten sechs Minuten zeigen wir dir, wie du deine Zweifel aus dem Weg räumst.
Inhaltsübersicht
Stabilitätsüberprüfung durch den Festigkeitsnachweis
Als allererstes solltest du folgendes wissen: Bei der Berechnung und Auslegung von Maschinenelementen spielt vor allem Forschung und Erfahrung eine wichtige Rolle. Durch Untersuchungen und Experimente wurden einige Kennwerte ermittelt, die mittlerweile allgemein gültig sind und deshalb in vielen Formeln Verwendung finden. All diese Kennwerte sind mit Hilfe von Tabellen festgehalten worden, um sie jederzeit nachschlagen zu können. Auch wir werden solche Tabellen verwenden. In diesem und allen weiteren Videos der Playlist beziehen wir uns dabei auf das Fach- und Tabellen-Buch „Roloff Matek“. Unsere Angaben sind auf die 22. Auflage des Springer Vieweg Verlages bezogen. Falls du mit Tabellen aus einer anderen Quelle arbeiten solltest, ist das kein Problem. Wir werden dir die jeweilige Tabelle immer einblenden, damit du weißt, welche Tabelle es in deiner Ausgabe ist.
Stabilität einer Kleiderstange
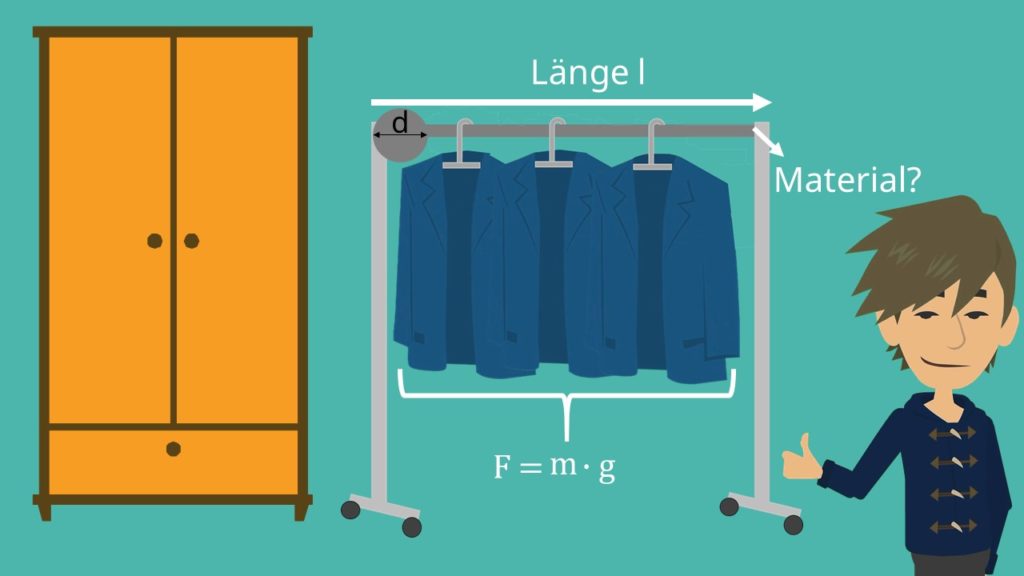
So, kommen wir jetzt zurück zu deinem Kleiderschrank. Um zu überprüfen, ob deine Kleiderstange die ganze Klamottenlast aushält, musst du zuerst einmal deine Stange vermessen. Zum weiteren Vorgehen brauchst du nämlich den Durchmesser und die Länge der Stange. Zudem benötigst du das Material, aus dem die Stange gefertigt worden ist. So, jetzt musst du nur noch wissen wie schwer deine Klamotten sind, um die Last zu berechnen, die die Welle aushalten muss. Die Last, also die Kraft, die auf die Stange wirkt, ist dann F=m*g, wobei m das Gewicht deiner Kleidung ist. So, da du nun all diese Werte ermittelt hast, kannst du beginnen die Stange anhand des statischen Festigkeitsnachweises auf ihre Stabilität zu überprüfen.
Dein Festigkeitsnachweis ist deswegen statisch, weil sich deine Stange nicht dreht, sondern fest an den Seiten verbaut ist. Somit treten keine zusätzlichen Belastungen durch die Dynamik auf. Du kennst zwar schon deine Kraft F, die an der Kleiderstange angreift, aber du musst auch wissen, welcher Belastungsfall vorliegt. Beim statischen Festigkeitsnachweis werden rein die Biege- und die Torsionsbelastung betrachtet. Da in unserem Fall beide Belastungen vorliegen, müssen wir auch beide in die Berechnung mit einbeziehen. Zum einen biegt sich nämlich die Stange durch die Gewichtskraft durch. Zum anderen verdreht sich die Stange ineinander, wenn du deine Klamotten nicht gleichmäßig auf den Kleiderbügel hängst. Damit haben wir auch eine Torsion.
Berechnung der Spannungen
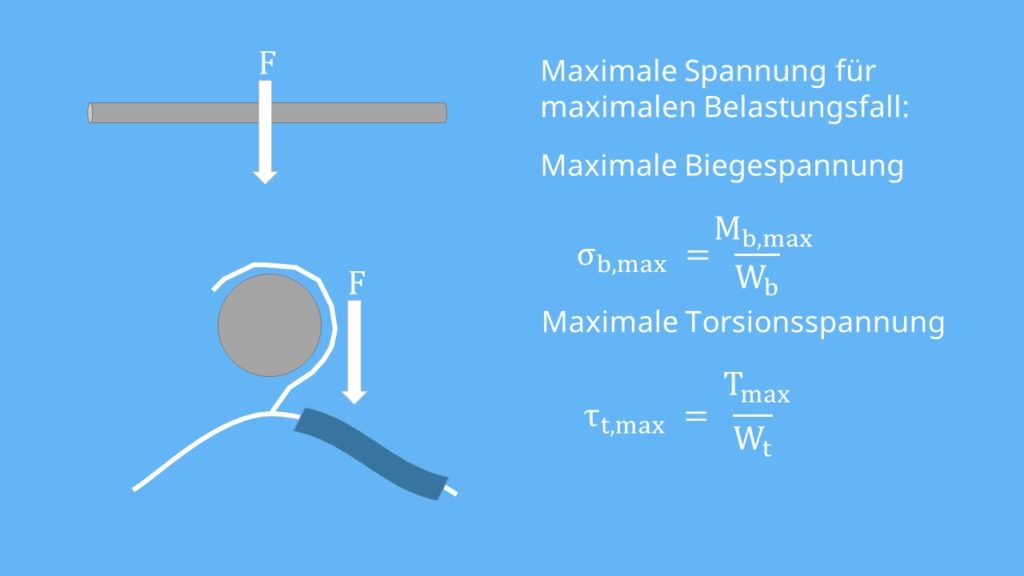
Wenn du dir über die Belastungsfälle Gedanken gemacht hast, kannst du auch schon die jeweiligen Spannungen berechnen. Dabei ist es wichtig, immer die maximale Spannung zu betrachten, da wir ja wissen wollen, ob die Stange auch noch im schlimmsten Fall, also total überfüllt, hält. Die maximale Biegespannung 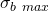 berechnest du mit
berechnest du mit 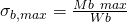 und die maximale Torsionsspannung
und die maximale Torsionsspannung  mit
mit 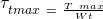 . Die Biege- und Torsionsmomente werden immer mit „Kraft mal Hebel“ berechnet, wobei der Hebel L1 den Abstand zur Einspannung und der Hebel L2 den seitlichen Abstand der Kleidung zur Stange beschreibt. Damit bekommst du für
. Die Biege- und Torsionsmomente werden immer mit „Kraft mal Hebel“ berechnet, wobei der Hebel L1 den Abstand zur Einspannung und der Hebel L2 den seitlichen Abstand der Kleidung zur Stange beschreibt. Damit bekommst du für 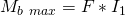 und für
und für 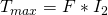 .
. 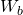 , beziehungsweise
, beziehungsweise 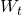 sind die sogenannten Widerstandsmomente für Biegung und Torsion. Sie liefern eine Aussage darüber, wie stark der Widerstand ist, den das Werkstück gegen die Biegung oder Torsion liefert. Sie sind deshalb auch sehr stark von der Geometrie des Werkstücks abhängig.
sind die sogenannten Widerstandsmomente für Biegung und Torsion. Sie liefern eine Aussage darüber, wie stark der Widerstand ist, den das Werkstück gegen die Biegung oder Torsion liefert. Sie sind deshalb auch sehr stark von der Geometrie des Werkstücks abhängig.
Sicherheit gegen Fließen
Da unsere Kleiderstange im Querschnitt einen Kreis ergibt, lauten die Formeln 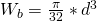 und
und 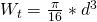 . Als nächstes müssen wir die Biege- und Torsionsfließgrenze berechnen. Die Formeln dafür lauten
. Als nächstes müssen wir die Biege- und Torsionsfließgrenze berechnen. Die Formeln dafür lauten 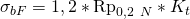 und
und 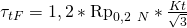 . Dafür benötigst du die Dehngrenze
. Dafür benötigst du die Dehngrenze 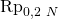 sowie den Korrekturfaktor
sowie den Korrekturfaktor 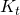 . Dein
. Dein 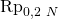 hängt vom Werkstoff ab. Du kannst es aus der Tabelle 1-1 ablesen. Mit deinem Stangendurchmesser und deiner werkstoffabhängigen Dehn- beziehungsweise Streckgrenze kannst du dann aus Tabelle 3-11 dein
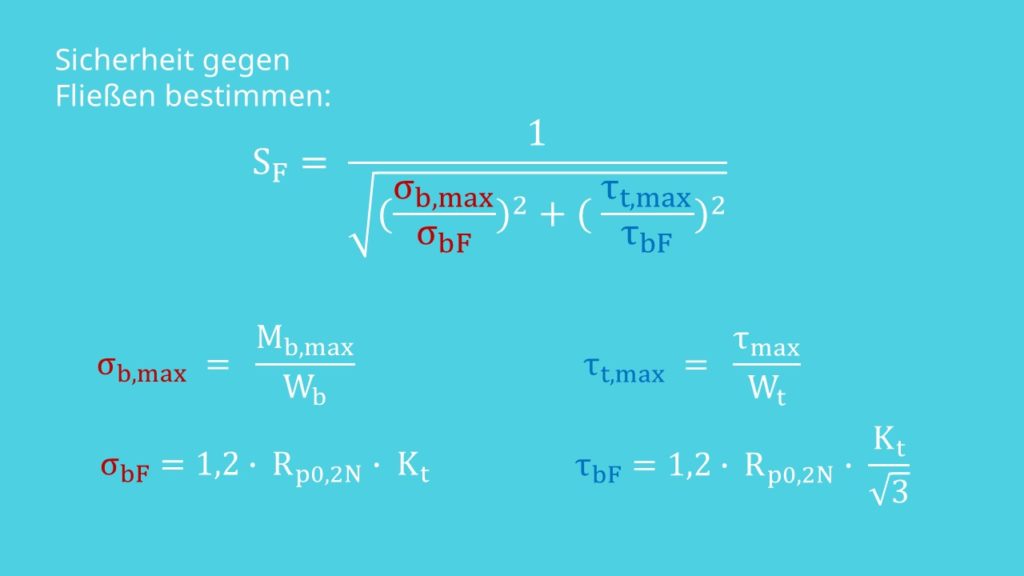
hängt vom Werkstoff ab. Du kannst es aus der Tabelle 1-1 ablesen. Mit deinem Stangendurchmesser und deiner werkstoffabhängigen Dehn- beziehungsweise Streckgrenze kannst du dann aus Tabelle 3-11 dein 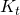 bestimmen. So, jetzt kannst du endlich deine Sicherheit gegen Fließen berechnen, mit
bestimmen. So, jetzt kannst du endlich deine Sicherheit gegen Fließen berechnen, mit 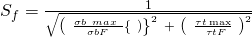 .
.
Und jetzt wird’s spannend! Wenn deine berechnete Sicherheit gegen Fließen größer oder genau so groß wie die erforderliche Mindestsicherheit gegen Fließen ist, dann hält deine Stange. Es muss also dein 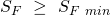 sein, damit du deine Kleidung ohne Bedenken aufhängen kannst. Die Werte für
sein, damit du deine Kleidung ohne Bedenken aufhängen kannst. Die Werte für 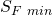 bekommst du aus Tabelle 3-14. Und… wie sieht’s aus? Wenn deine berechnete Sicherheit zu klein sein sollte, dann versuch es mal mit einem größeren Stangendurchmesser oder einem anderen Material.
bekommst du aus Tabelle 3-14. Und… wie sieht’s aus? Wenn deine berechnete Sicherheit zu klein sein sollte, dann versuch es mal mit einem größeren Stangendurchmesser oder einem anderen Material.
So, jetzt weißt du nicht nur wie du sämtliche Wellen oder Kleiderstangen berechnen kannst, sondern auch, was du ändern könntest, damit du eine höhere Sicherheit bekommst. Bis bald!