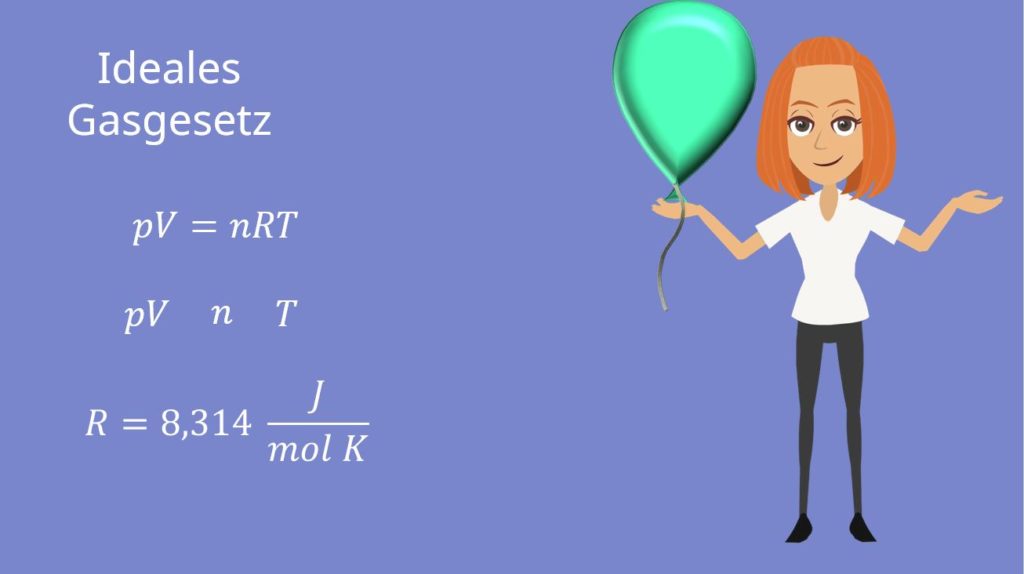Thermodynamische Zustandsgrößen und Grundgleichungen
Dass ein Thermometer auf Basis des Nullten Hauptsatzes funktioniert, weißt du sicherlich. Doch was genau haben die Begriffe Zustandsgrößen, thermisches Gleichgewicht, ideale Gasgleichung und ideales Gasgesetz mit dessen Funktionsweise zu tun? Das erfährst du alles hier.
Inhaltsübersicht
Wie ist die ideale Gasgleichung und das ideales Gasgesetz definiert?
Du kennst bereits die Masse m und das Volumen V, doch damit dir alle Zustandsgrößen bekannt sind, gehen wir noch auf die Temperatur T und den Druck p ein.
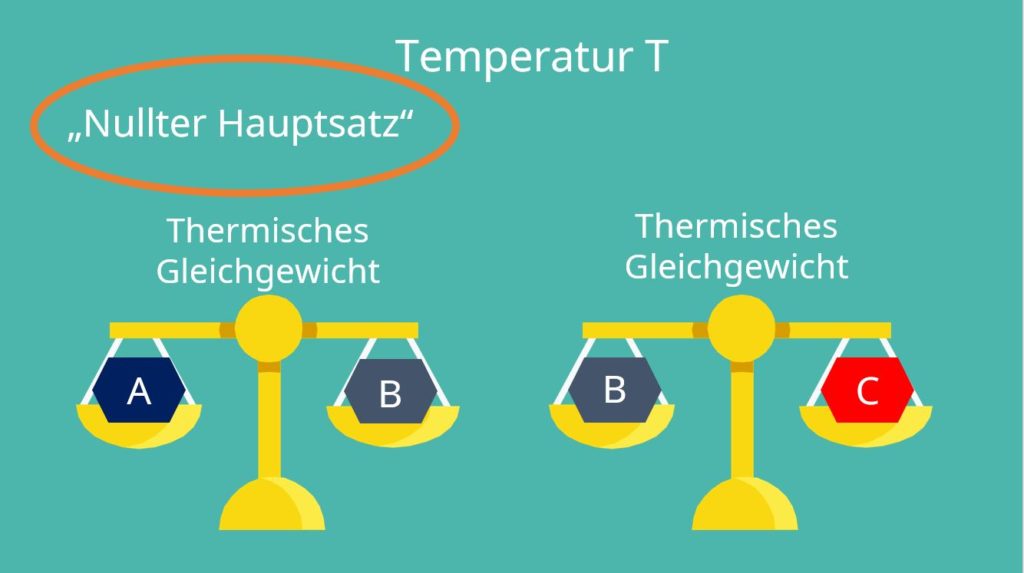
Die Temperatur können wir allerdings nicht so einfach angeben wie die Zustandsgrößen Masse und Volumen. Deshalb benötigen wir den Nullten Hauptsatz. Dieser besagt: Wenn zwei Systeme A und B im thermischen Gleichgewicht stehen und auch B und ein weiteres System C das thermische Gleichgewicht aufweisen, dann stehen auch A und C im thermischen Gleichgewicht. Dies ist auch eine wichtige Beobachtung im Zusammenhang mit den Begrifflichkeiten Ideale Gasgleichung bzw. Ideales Gasgesetz.
Funktionsweise Thermometer und thermisches Gleichgewicht
Das klingt jetzt natürlich etwas komplex, bildet aber die Grundlage, warum Thermometer überhaupt funktionieren, denn das hängt mit dem Phänomen Thermisches Gleichgewicht zusammen. Das Glas um die Flüssigkeit hat die gleiche Temperatur wie die Umgebung und auch die gleiche Temperatur wie die Flüssigkeit. Das heißt, das Glas ist mit der Umgebung und der Flüssigkeit im Gleichgewicht und damit haben auch die Flüssigkeit und die Umgebung ein thermisches Gleichgewicht.
Daraus können wir ableiten, dass wir die Temperatur anhand von Fixpunkten bilden. Bei der Skala nach Celsius wurde das durch den Gefrierpunkt und den Verdampfungspunkt von Wasser gemacht. In der Thermodynamik verwenden wir die Skala nach Kelvin. Diese hat als Fixpunkte den absoluten Nullpunkt, also die geringste Temperatur, die erreicht werden kann, und den sogenannten Tripelpunkt von Wasser. Der absolute Nullpunkt liegt bei - 273,15 Grad Celsius. Von Vorteil ist für uns, dass die Schrittweite bei beiden Skalen gleich ist. Das heißt: Erhöhen wir die Temperatur um einen Grad Celsius, erhöhen wir auch um ein Grad Kelvin.
Funktionsweise Ballon und mechanisches Gleichgewicht
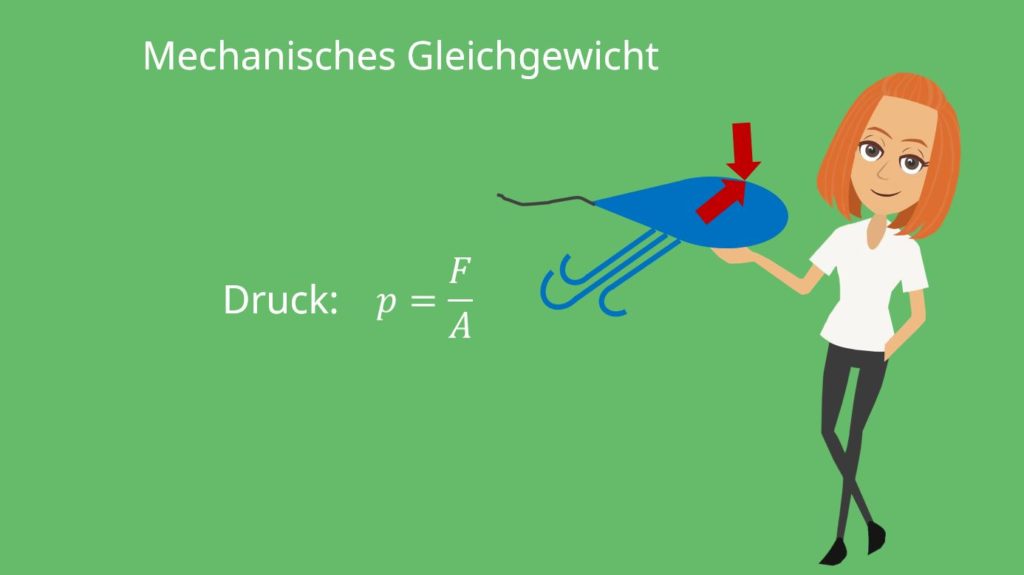
Wir kennen jetzt den Begriff Thermisches Gleichgewicht und wissen grob, was die Zustandsgrößen sind, was wir für die ideale Gasgleichung noch brauchen werden. Jetzt ist dir sicher noch das mechanische Gleichgewicht durch Kräfte bekannt. Wir verwenden hier jetzt einfach nur die Zustandsgröße Druck, also teilen durch eine Fläche. Klingt jetzt erstmal merkwürdig, aber in der Thermodynamik haben wir es selten mit Kräften alleine zu tun.
Betrachten wir dazu einen Luftballon: Dieser hat im Inneren einen höheren Druck als die Umgebung. Öffnen wir den Ballon, strömt solange Luft hinaus, bis der Druck im Inneren gleich dem Äußeren entspricht. Genau dann befinden wir uns im mechanischen Gleichgewicht, denn dann drückt von innen genau die gleiche Kraft auf den Ballon wie von außen.
Extensive und intensive Zustandsgrößen
Die Zustandsgrößen Masse, Volumen, Temperatur und Druck, die wir später noch für den Themenblock Ideale Gasgleichung bzw. Ideales Gasgesetz brauchen, können wir nun auch klassifizieren. Um das zu machen, betrachten wir einfach zwei Becher Kaffee: Beide haben die Temperatur 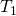 , die Masse
, die Masse 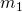 und das Volumen
und das Volumen 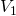 . Der Druck ist in beiden Bechern
. Der Druck ist in beiden Bechern 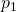 . Das heißt: Die beiden Becher sind erstmal gleich.
. Das heißt: Die beiden Becher sind erstmal gleich.
Als nächstes wollen wir die Becher zusammen in einen großen Becher kippen und uns die Zustandsgrößen nochmal anschauen. Du weißt ja sicher, dass sich die Masse 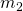 und das Volumen
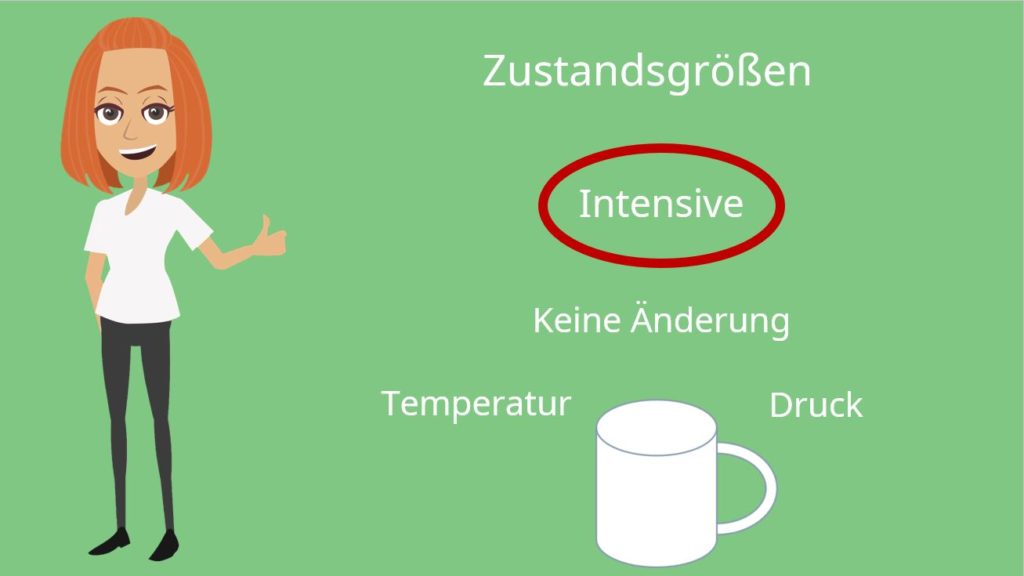
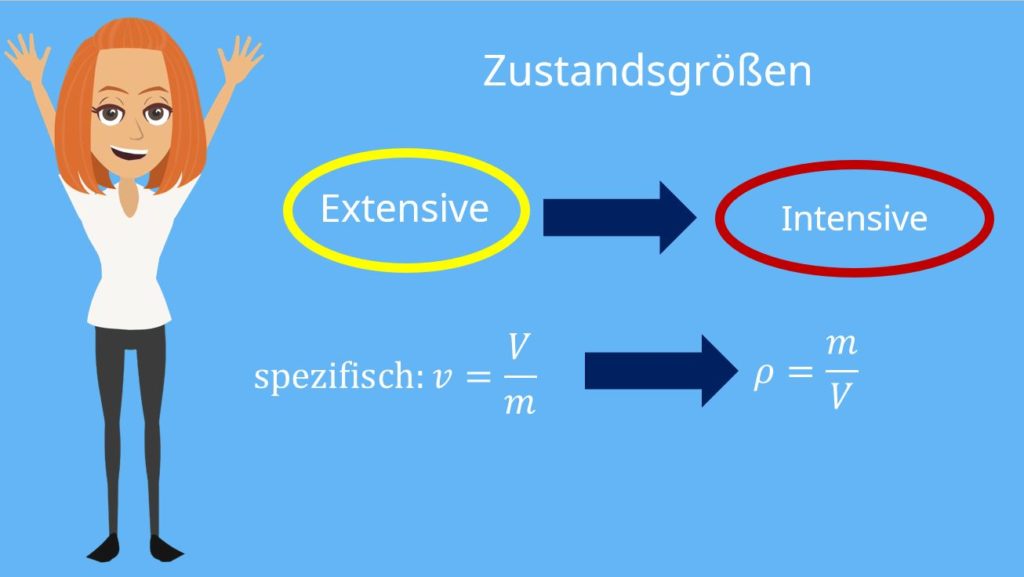
und das Volumen 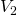 aus den beiden Massen beziehungsweise Volumina der beiden Becher ergeben. Doch die Temperatur und der Druck bleiben unverändert. Nun können wir die Zustandsgrößen klassifizieren. Wir unterscheiden in sogenannte intensive und extensive Zustandsgrößen. Intensive Zustandsgrößen ändern sich nicht mit der Systemgröße. In unserem Fall sind das die Zustandsgrößen Temperatur und der Druck. Diese sind schließlich bei dem Kaffeeexperiment gleichgeblieben.
aus den beiden Massen beziehungsweise Volumina der beiden Becher ergeben. Doch die Temperatur und der Druck bleiben unverändert. Nun können wir die Zustandsgrößen klassifizieren. Wir unterscheiden in sogenannte intensive und extensive Zustandsgrößen. Intensive Zustandsgrößen ändern sich nicht mit der Systemgröße. In unserem Fall sind das die Zustandsgrößen Temperatur und der Druck. Diese sind schließlich bei dem Kaffeeexperiment gleichgeblieben.
Du kannst dir dann sicher denken, dass Volumen und Masse extensive Zustandsgrößen sein müssen. Und wie kann man sich merken, ob extensive Zustandsgrößen systemabhängig sind oder nicht? Dafür haben wir eine Eselsbrücke: Das Volumen ist eine extensive Zustandsgröße. Denn wenn du das vergrößerst, „EX“-pandierst du. Das „EX“ gibt dir also den Hinweis dazu.
Aus extensiven Zustandsgrößen kannst du schnell intensive Zustandsgrößen machen, indem du den Quotienten bildest. Als Beispiel nehmen wir das spezifische Volumen: Es ist der Quotient aus Volumen und Masse und ist gleichzeitig auch der Kehrwert der Dichte. Und diese ändert sich natürlich nicht, nur weil wir das Doppelte an Kaffee haben.
Ideale Gasgleichung bzw. ideales Gasgesetz
Jetzt kennst du die Zustandsgrößen und kannst sie auch klassifizieren. Als nächstes wollen wir dir noch zwei wichtige Annahmen nahebringen: Ideale Gasgleichung bzw. ideales Gasgesetz und ideale Flüssigkeit.
Unter ideale Gasgleichung, oder auch ideales Gasgesetz, versteht man folgende Formel:
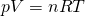
Die Ideales Gasgesetz Formel ist eine der wichtigsten der Thermodynamik! Diese wirst du noch ganz oft verwenden. pV, n und T sind dir als Zustandsgrößen bereits bekannt. R ist die sogenannte ideale Gaskonstante und hat den Wert 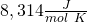 .
.
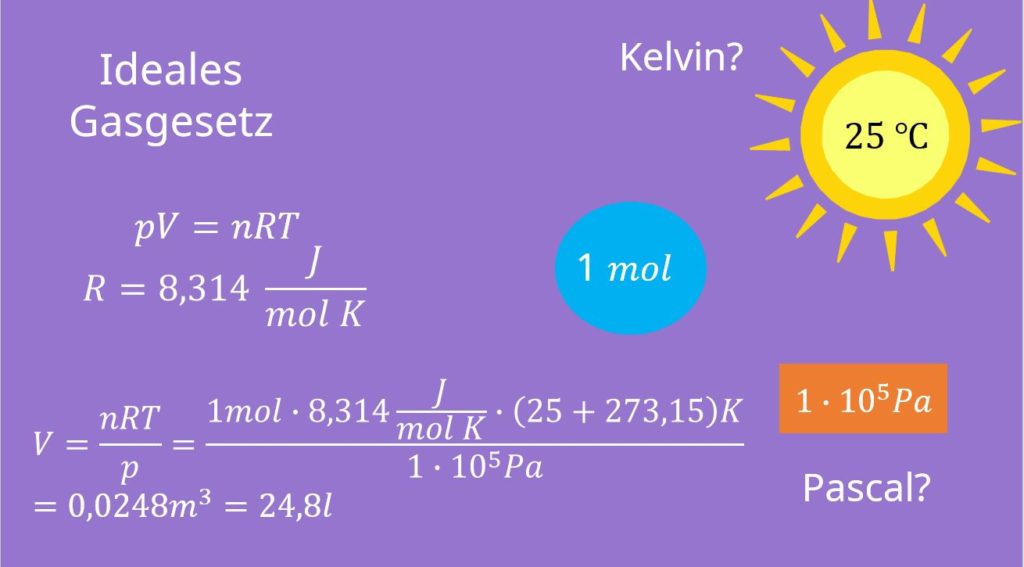
Was kannst du damit jetzt berechnen? Wir überlegen uns, dass wir ein Mol eines idealen Gases bei 25 Grad Celsius und einem bar haben. Damit kannst du dir sofort das Volumen berechnen. Aber Achtung: Die ideale Gaskonstante ist pro Kelvin und der Druck in bar gegeben! Wir müssen also noch die Temperatur in Kelvin und den Druck in Pascal umrechnen, bevor wir diese in die ideale Gasgleichung einsetzen können. Nach V umgeformt, erhalten wir aus dem idealen Gasgesetz:
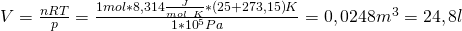
Diese Formel kann für fast jedes Gas angewendet werden.
Ideale Flüssigkeit
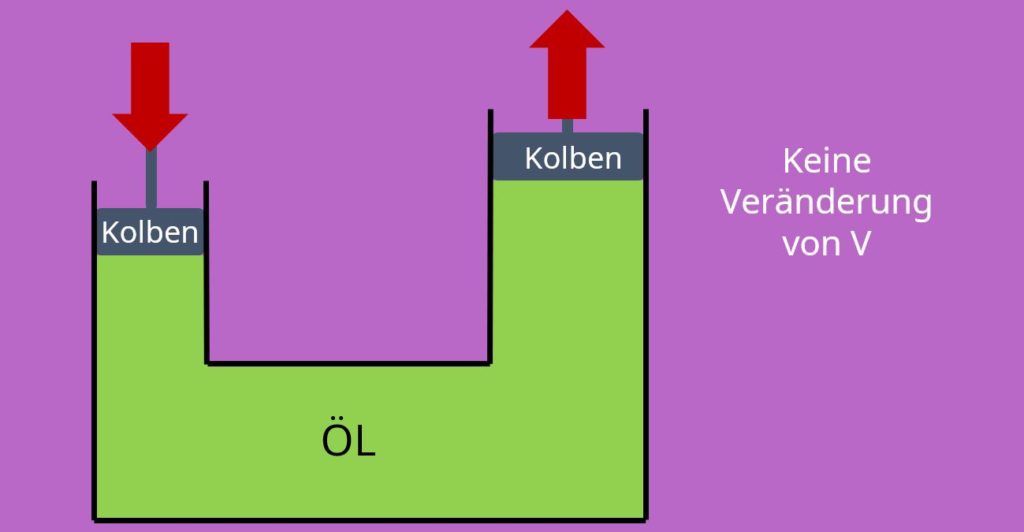
Nachdem uns die ideale Gasgleichung nun klar sein sollte, wenden wir uns als nächstes der idealen Flüssigkeit zu. Diese hat die Eigenschaft, dass das spezifische Volumen und damit auch die Dichte konstant sind. Wir betrachten also einen inkompressiblen Zustand und können bei jedem Druck davon ausgehen, dass wir immer das gleiche spezifische Volumen haben. Und das kann man in der Realität sogar sehen: Du hast doch bestimmt schon mal von Hydraulik gehört. Hier wird die Kraft mit Hilfe von Öl übertragen. Das geht nur, wenn das Öl sich nicht zusammendrücken kann, also sich sein spezifisches Volumen nicht ändert.
Stell dir mal vor, wir würden das mit einem Gas probieren: Das ganze würde nicht funktionieren, weil sich das Gas zusammendrücken lässt.
Damit kennst du dich nun bestens mit den Zustandsgrößen aus, kennst das Phänomen Thermisches Gleichgewicht und weißt genau, was ideale Gasgleichung bzw. ideales Gasgesetz eigentlich bedeuten.