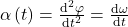Winkelbeschleunigung
In dem folgenden Artikel erklären wir dir wie sich Winkelbeschleunigung zusammensetzt, in welcher Einheit man sie angibt und wie man sie berechnet.
Falls du das Thema lieber in einem Video erklärt bekommen möchtest, dann schau doch hier mal rein.
Inhaltsübersicht
Winkelbeschleunigung Definition
Die Winkelbeschleunigung beschreibt die zeitliche Änderung der Winkelgeschwindigkeit. Dies bedeutet, dass die Winkelbeschleunigung die Ableitung der Winkelgeschwindigkeit nach der Zeit ist.
Mathematisch kann dieser Zusammenhang zwischen Winkelgeschwindigkeit 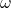 und Winkelbeschleunigung
und Winkelbeschleunigung 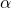 durch die zeitliche Ableitung ausgedrückt werden.
durch die zeitliche Ableitung ausgedrückt werden.
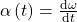
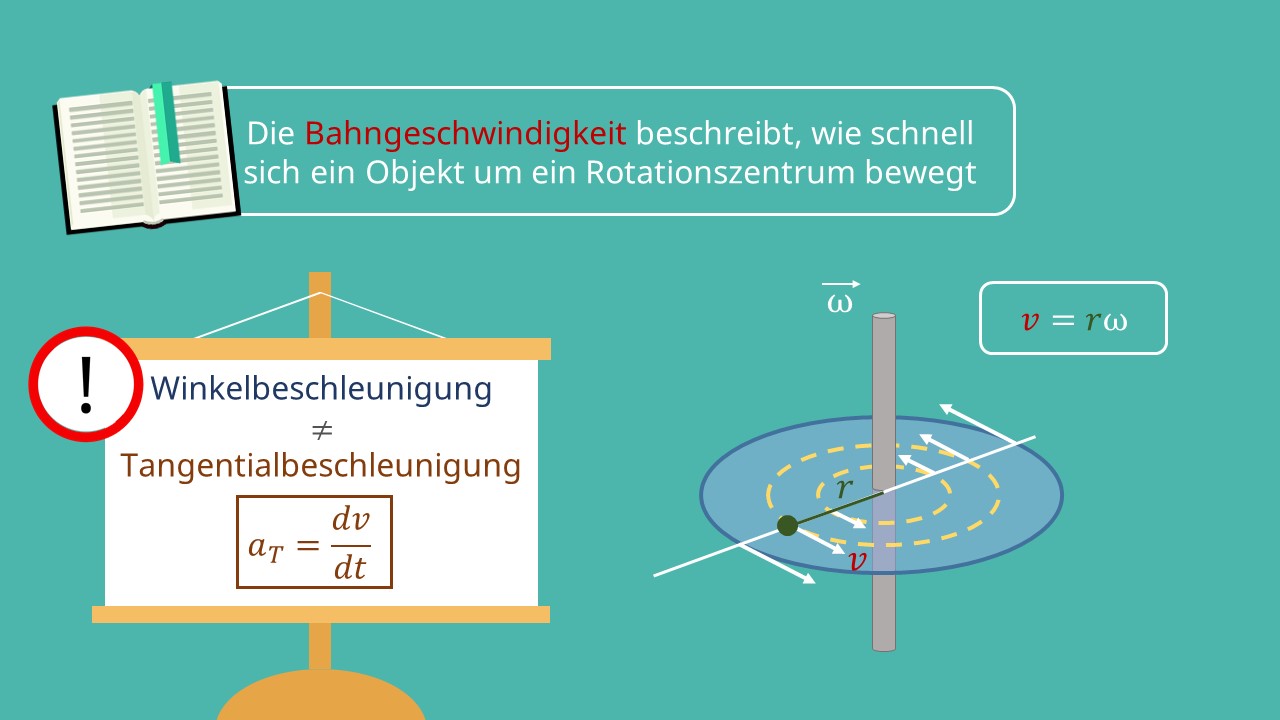
Die Winkelbeschleunigung darf nicht mit der Tangentialbeschleunigung 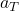 verwechselt werden, welche die Ableitung der Bahngeschwindigkeit darstellt,
verwechselt werden, welche die Ableitung der Bahngeschwindigkeit darstellt,
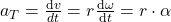
wobei r den Abstand zur Rotationsachse repräsentiert. Betrachtet man eine Kreisbewegung, so zeigt die Winkelbeschleunigung in die tangentiale Richtung. Zusätzlich zur Winkelbeschleunigung, wirkt auf den Körper auch noch die sogenannte Radialbeschleunigung , oder auch Zentripetalbeschleunigung genannt. Die Radialbeschleunigung und Winkelbeschleunigung sind senkrecht zueinander.
Da bei einer Kreisbewegung die Geschwindigkeit immer tangential zur Kreisbewegung ist, ändert die Geschwindigkeit ständig ihre Richtung. Die Geschwindigkeit wird andauernd zum Kreismittelpunkt hin beschleunigt. Diese Beschleunigung wird Radialbeschleunigung genannt. Die Gesamtbeschleunigung bei einer Kreisbewegung kann dann durch die Summe der Winkelbeschleunigung und der Radialbeschleunigung ausgedrückt werden.
Winkelbeschleunigung Formel
Die Winkelbeschleunigung 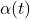 lässt sich mathematisch wie folgt ausdrücken.
lässt sich mathematisch wie folgt ausdrücken.
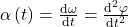
Wenn 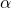 konstant ist, also wenn der Quotient aus der Änderung der Winkelgeschwindigkeit und der Änderung der Zeit konstant ist, dann spricht man von einer Kreisbewegung mit konstanter Beschleunigung.
konstant ist, also wenn der Quotient aus der Änderung der Winkelgeschwindigkeit und der Änderung der Zeit konstant ist, dann spricht man von einer Kreisbewegung mit konstanter Beschleunigung.
Winkelbeschleunigung Einheit
Die Einheit der Winkelbeschleunigung ergibt sich aus der letztgenannten Formel zu
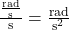
da die Winkelbeschleunigung das Verhältnis der Änderung der Winkelgeschwindigkeit und der Änderung der Zeit beschreibt.
Winkelbeschleunigung berechnen
Zwischen der Winkelbeschleunigung, dem Drehmoment M und dem Trägheitsmoment I besteht eine enge Beziehung, welche folgende Formel zum Ausdruck bringt

Möchtest du mehr über das Drehmoment wissen, dann schau unseren extra Beitrag
Drehmoment
dazu an. Nach der Eulersche’n Gleichung, entspricht die Änderung des Drehimpulses gerade dem Moment 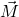 , so dass man folgenden Zusammenhang zwischen Drehimpuls und Winkelbeschleunigung erhält
, so dass man folgenden Zusammenhang zwischen Drehimpuls und Winkelbeschleunigung erhält
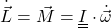
Interessiert dich, was der Drehimpuls physikalisch beschreibt und wie du ihn berechnen kannst, dann schau unseren extra Beitrag Drehimpuls dazu an.
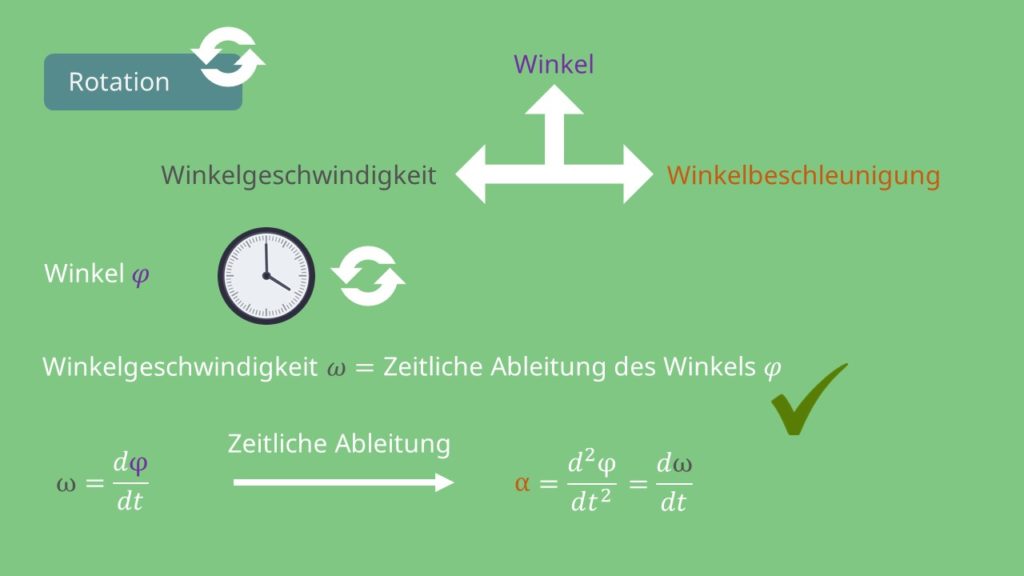
Winkel, Winkelgeschwindigkeit und Winkelbeschleunigung
Im Folgenden wird noch einmal übersichtlich der Zusammenhang zwischen dem Rotationswinkel 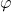 , der Winkelgeschwindigkeit
, der Winkelgeschwindigkeit 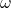 und der Winkelbeschleunigung \alpha dargestellt. Geht man von einem Rotationswinkel
und der Winkelbeschleunigung \alpha dargestellt. Geht man von einem Rotationswinkel 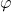 aus, dann kann daraus die Winkelgeschwindigkeit berechnet werden, indem man die Winkelgeschwindigkeit nach der Zeit ableitet
aus, dann kann daraus die Winkelgeschwindigkeit berechnet werden, indem man die Winkelgeschwindigkeit nach der Zeit ableitet
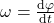
Durch weiteres einmaliges Ableiten der Winkelgeschwindigkeit nach der Zeit, erhält man dann die Winkelbeschleunigung 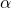
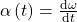
Dies ist gleichbedeutend mit der zweimaligen zeitlichen Ableitung des Rotationswinkels 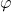 . Die Winkelbeschleunigung \alpha lässt sich also auch in Abhängigkeit des Rotationswinkels
. Die Winkelbeschleunigung \alpha lässt sich also auch in Abhängigkeit des Rotationswinkels 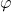 wie folgt ausdrücken
wie folgt ausdrücken