Zentripetalkraft und Zentrifugalkraft
Der Unterschied zwischen der Zentripetalkraft und Zentrifugalkraft ist essenziell, um eine Kreisbewegung zu verstehen. In diesem Artikel wollen wir diesen Unterschied erklären. Im Anschluss gehen wir auf die Zentripetalkraft und Zentrifugalkraft im Einzelnen ein.
Wenn du mehr dazu wissen willst, dann schau dir doch unser Video dazu an. Hier erklären wir dir alles in kürzester Zeit!
Inhaltsübersicht
Kreisbewegung
Neben der Schwingung und einer geradlinigen Bewegung ist die Kreisbewegung eine der wichtigsten Bewegungsarten. Hierbei bewegt sich eine Masse auf einer Bahnkurve um einen festgelegten Mittelpunkt. Dies ist eine Form der Rotation.
Als eine gleichförmige Kreisbewegung wird eine Masse bezeichnet, die sich mit einem konstanten Betrag der Bahngeschwindigkeit 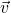 fortbewegt. Es wird der Betrag der Geschwindigkeit betrachtet, da sich bei einer Rotation die Richtung des Vektors ständig ändert. Aufgrund der Richtungsänderung wird auch oft von einer beschleunigten Kreisbewegung gesprochen. Beschleunigt ist sie, da sich die Richtung der Geschwindigkeit ständig ändert, obwohl die Länge des Geschwindigkeitsvektors gleichbleibt. Mehr zum Thema Beschleunigung
findest du in einem extra Video.
fortbewegt. Es wird der Betrag der Geschwindigkeit betrachtet, da sich bei einer Rotation die Richtung des Vektors ständig ändert. Aufgrund der Richtungsänderung wird auch oft von einer beschleunigten Kreisbewegung gesprochen. Beschleunigt ist sie, da sich die Richtung der Geschwindigkeit ständig ändert, obwohl die Länge des Geschwindigkeitsvektors gleichbleibt. Mehr zum Thema Beschleunigung
findest du in einem extra Video.
Unterschied Zentripetalkraft Zentrifugalkraft
Die Zentripetalkraft und Zentrifugalkraft wirken bei einer beschleunigten Kreisbewegung und haben die gleiche Formel. Es handelt sich um entgegengesetzte Kräfte, die abhängig von dem Bezugssystem sind. Wird eine Kreisbewegung von außen betrachtet, wirkt nur die Zentripetalkraft. Befindet sich der Beobachter im rotierenden System nimmt er beide Kräfte wahr.
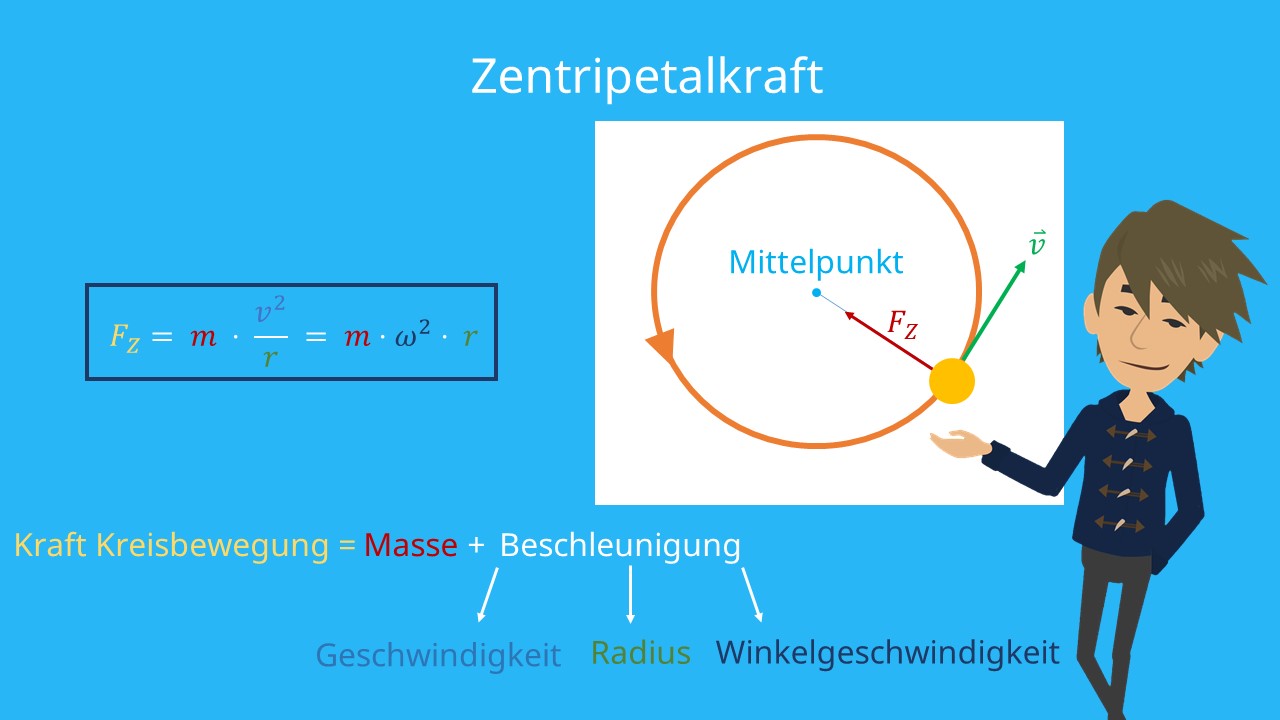
Zentripetalkraft Formel
Die Kraft, welche einen Körper auf eine Kreisbahn zwingt, wird Zentripetalkraft genannt. Sie ist stets senkrecht zum Geschwindigkeitsvektor und zum Kreismittelpunkt gerichtet.
Ohne diese Kraft würde sich der Körper statt auf einer Bahnkurve, in Richtung des Geschwindigkeitsvektors, also tangential zur Kreisbahn, wegbewegen.
Entsteht nun eine gleichförmige Kreisbewegung, so ist der Betrag der Bahngeschwindigkeit immer gleich groß und steht sowohl auf dem Radius r als auch auf der Zentripetalkraft 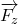 senkrecht. Die Herleitung der Kraft erfolgt durch eine grafische Verschiebung. Die Zentripetalkraft Formel ist:
senkrecht. Die Herleitung der Kraft erfolgt durch eine grafische Verschiebung. Die Zentripetalkraft Formel ist:
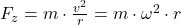
Dabei ist  der Radius des Kreises, welcher den Weg der Bewegung beschreibt und
der Radius des Kreises, welcher den Weg der Bewegung beschreibt und 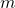 die Masse des Körpers.
die Masse des Körpers.  ist die Winkelgeschwindigkeit
. Die Geschwindigkeit, die in der Berechnung verwendet wird, sollte als Skalar gegeben sein oder entspricht der Länge des Geschwindigkeitsvektors.
ist die Winkelgeschwindigkeit
. Die Geschwindigkeit, die in der Berechnung verwendet wird, sollte als Skalar gegeben sein oder entspricht der Länge des Geschwindigkeitsvektors.
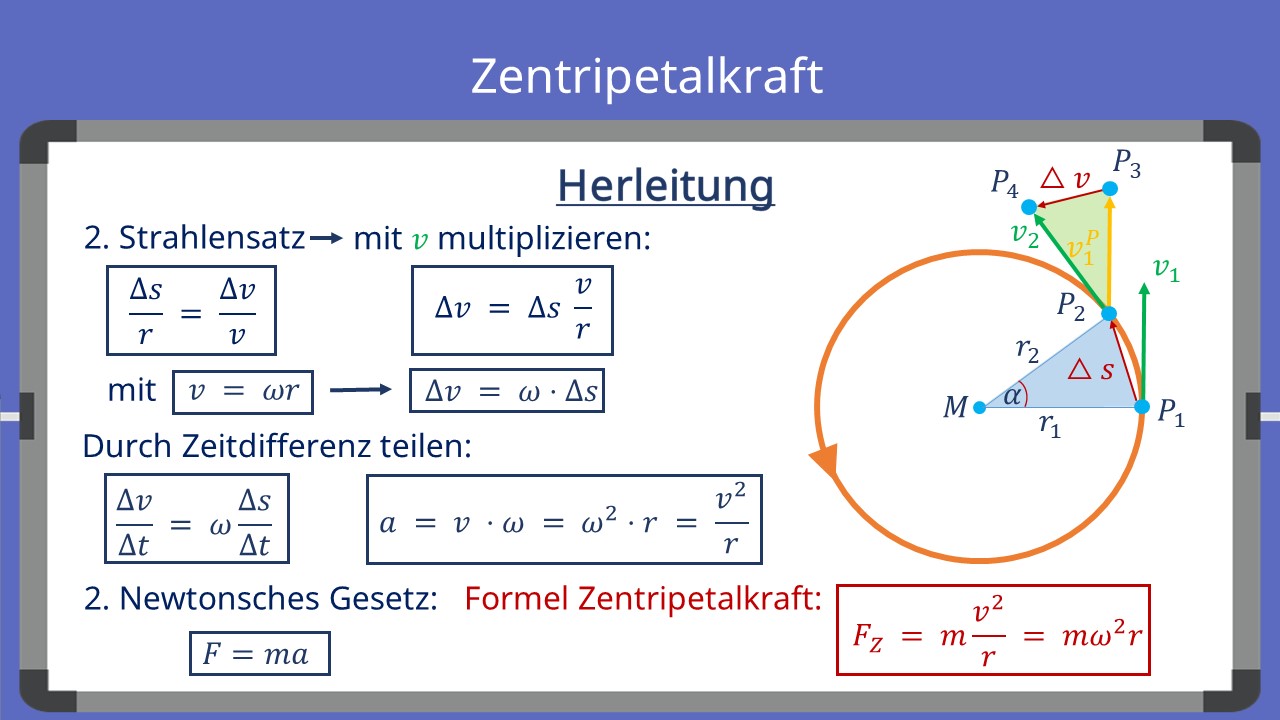
Herleitung Zentripetalkraft
In diesem Kapitel geht es nicht um die Vektoren, sondern lediglich um deren Länge. So können nur Skalare betrachtet und die vektorielle Schreibweise vernachlässigt werden.
Die Kreisbewegung beginnt auf der ersten Position 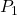 und endet auf der zweiten
und endet auf der zweiten 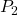 . Dabei hat der Körper die Wegstrecke
. Dabei hat der Körper die Wegstrecke  auf dem Kreis in einer bestimmten Zeit
auf dem Kreis in einer bestimmten Zeit 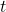 zurückgelegt. Die direkte Verbindung von
zurückgelegt. Die direkte Verbindung von 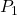 nach
nach 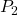 wird
wird 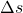 genannt. Das physikalische Objekt hatte an der ersten Position eine Geschwindigkeit von
genannt. Das physikalische Objekt hatte an der ersten Position eine Geschwindigkeit von 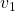 und an der zweiten
und an der zweiten 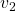 . Beide Geschwindigkeiten sind gleich groß, zeigen aber in unterschiedliche Richtungen.
. Beide Geschwindigkeiten sind gleich groß, zeigen aber in unterschiedliche Richtungen.
Nun findet eine Parallelverschiebung des ersten Geschwindigkeitsvektors statt, sodass 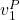 entsteht. Außerdem entstehen die Positionen drei
entsteht. Außerdem entstehen die Positionen drei 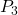 und vier
und vier 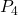 . Die direkte Verbindung der beiden letzten Positionen erzeugt die Differenz der Geschwindigkeiten
. Die direkte Verbindung der beiden letzten Positionen erzeugt die Differenz der Geschwindigkeiten 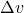 .
.
Über den zweiten Strahlensatz kann folgende Beziehung aufgestellt werden:
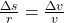
Jetzt wird mit  multipliziert
multipliziert
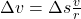
und die Umlaufgeschwindigkeit mit der Winkelgeschwindigkeit 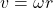 der Kreisebene eingesetzt:
der Kreisebene eingesetzt:
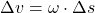
Nun wird durch die Zeit 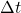 , die der Körper von
, die der Körper von 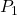 nach
nach 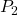 braucht, geteilt.
braucht, geteilt.
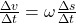
Geschwindigkeit durch Zeit gibt die Definition einer Beschleunigung 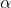 wieder. Genauso spiegelt der Weg durch die Zeit die Geschwindigkeit wider. Somit ergibt sich:
wieder. Genauso spiegelt der Weg durch die Zeit die Geschwindigkeit wider. Somit ergibt sich:
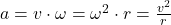
Nach dem zweiten Newtonschen Gesetz gilt für eine Kraft:
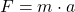
Falls du nicht mehr genau über die Gesetze Bescheid weißt, haben wir dir hier unseren Beitrag zu den Newtonschen Axiomen
verlinkt. Mit dieser Definition kann die Formel der Zentripetalkraft 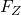 aufgestellt werden:
aufgestellt werden:
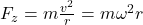
Zentripetalkräfte Beispiel
Die Zentripetalkraft wirkt in Richtung des Mittelpunktes einer Kreisbewegung. So zum Beispiel auch zwischen Mond und Erde. Die Erde zwingt den Mond durch die Gravitationskraft auf seine Bahnkurve.
Ein anderer Fall wäre ein Auto, welches eine Kurve durchfährt. Dabei wirkt eine Zentripetalkraft zum Kreismittelpunkt der Kurve. In diesem Fall die Haftreibungskraft. Ohne diese wäre eine Kurvenfahrt nicht möglich und das Auto würde sich aus der Kurve bewegen.
Zentrifugalkraft Formel
Für die Definition der Zentrifugalkraft spielt das gewählte Bezugssystem eine wichtige Rolle. Von diesem wird die Kreisbewegung aus beschrieben. Das System dient dazu, ortsabhängige Größen der Bewegung festzulegen. Des Weiteren wird die Zentrifugalkraft auch Fliehkraft genannt und sie ist eine Trägheitskraft.
Befindet sich der Beobachter im Bezugssystem außerhalb der Kreisbewegung, nimmt dieser nur die Zentripetalkraft wahr. Wenn der Beobachter sich jedoch im Bezugssystem des beschleunigten Systems befindet, so verspürt dieser zum einen die Zentripetalkraft und zum anderen auch eine Kraft, welche ihn nach außen treibt, die sogenannte Zentrifugalkraft. Sie ist der Zentripetalkraft entgegen gerichtet. Die Kraft wird also nur von jemanden wahrgenommen, der sich selbst im rotierenden System befindet.
Die Zentrifugalkraft hat dieselbe Formel, wie die Zentripetalkraft:
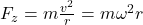
Aufgepasst werden muss bei der Lage des Bezugssystems. Je nach Notwendigkeit muss ein negatives Vorzeichen hinzugefügt werden.
Scheinkraft
Die Zentrifugalkraft wird auch als Scheinkraft bezeichnet, weil sie von der Wahl des Bezugssystems abhängt, aus dem der physikalische Vorgang beobachtet wird. In einem beschleunigten Bezugssystem, welches sich in der Rotation befindet, wirkt die Kraft. Hingegen wirkt sie in einem nicht beschleunigten System nicht. Nicht beschleunigte Systeme werden auch Inertialsysteme genannt. Eine genauere Beschreibung dieser Art von Systemen findest du in unserem Artikel zu Inertialsystemen .
In den zwei verschiedenen Arten von Bezugssystemen gibt es noch einen Unterschied bezüglich den Newtonschen Axiomen . Jene gelten uneingeschränkt nur in Inertialsystemen, während sie in nicht beschleunigten nicht streng gelten. In beschleunigten gibt es nicht zu jeder Kraft eine Gegenkraft.
Zusammenfassend geht es also bei einer Scheinkraft um den Widerstand eines Körpers gegenüber Änderungen seines Bewegungszustandes. Aus diesem Grund wird auch oft von Trägheitskräften gesprochen. Diese ist von einem äußeren Bezugssystem nicht zu erfahren.
Kreisbewegung
Wie du bereits weißt, sind Zentripetalkraft und Zentrifugalkraft wichtige Kräfte innerhalb einer Kreisbewegung.
Wenn du erfahren möchtest, was eine Kreisbewegung grundsätzlich ausmacht und durch welche Größen du sie beschreiben kannst, dann schau dir gerne unseren Beitrag dazu an!