Zug- und Torsionsversuch
Du willst wissen was beim Zugversuch eigentlich passiert? Das erklären wir dir in diesem Beitrag
Inhaltsübersicht
Zerstörende Materialversuche
Materialgesetze beruhen, im Gegensatz zu Spannungen und Dehnungen, auf Versuchen. Das liegt daran, dass es unzählige verschiedene Materialien gibt und somit keine theoretischen Überlegungen mehr möglich ist. In der Regel werden dabei zwei Versuche durchgeführt, um eine Gesetzmäßigkeit zu bestimmen: Der Zugversuch und der Torsionsversuch.
Der Zugversuch
Beim Zugversuch wird ein Stab mit definierter Länge L und dem bekannten Querschnitt A eingespannt und mit einer Kraft F belastet. Die Kraft wird dabei kontinuierlich gesteigert.
Parallel dazu wird zu jeder Kraft eine Längenänderung 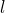 aufgezeichnet. Um nun ein geometrisch unabhängiges Materialgesetz zu erhalten, verwenden wir die Größen Spannung und Dehnung mit
aufgezeichnet. Um nun ein geometrisch unabhängiges Materialgesetz zu erhalten, verwenden wir die Größen Spannung und Dehnung mit
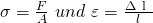
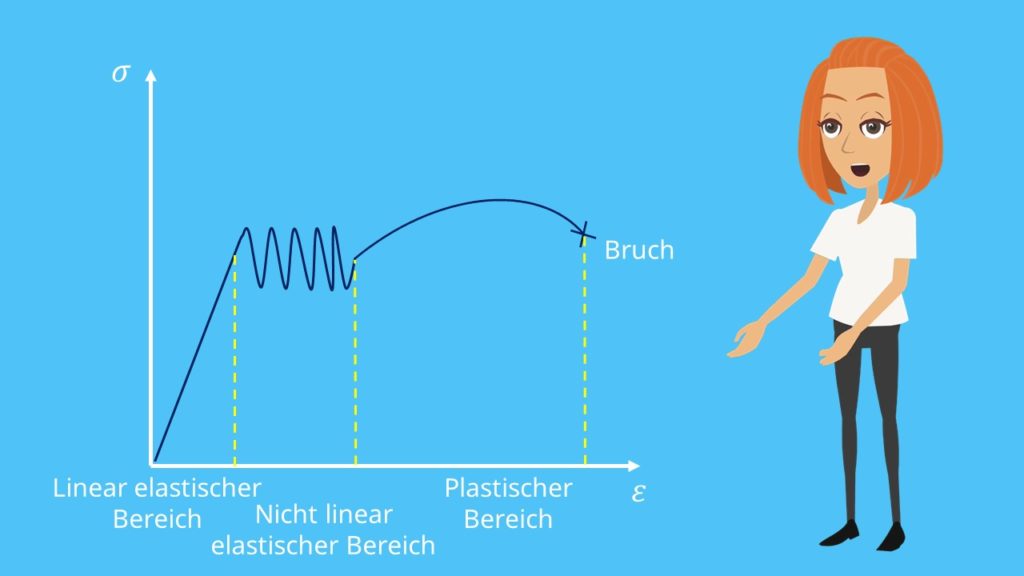
Mit den Daten, die du aus dem Zugversuch erhältst, können wir einen Graphen zeichnen. Diesen können wir grob in drei Bereiche einteilen:
Den linear elastischen Bereich: Dieser Zustand ist umkehrbar.
Den nicht linear elastischen Bereich und
Den plastischen Bereich: Dieser Zustand ist nicht umkehrbar, d.h. ab diesem Zeitpunkt kann das Material nicht mehr in seine ursprüngliche Form zurückkehren.
Wie du dir bestimmt denken kannst, wird das Material am Ende brechen.
Der Torsionsversuch
Beim Torsionsversuch spannen wir ein dünnwandiges Rohr der Länge L ein. Dieses Rohr wird mit einem Torsionsmoment belastet. Das heißt wir wollen das Rohr verdrehen. Hier wird dann der Verdrehwinkel 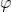 gemessen. Du erkennst sicher, dass wir bei der Torsion keine Normalspannungen erhalten können. Dementsprechend betrachten wir hier Schubspannungen. Da die Torsion ein Moment in x-Richtung ist, erhalten wir aus dem Momentengleichgewicht:
gemessen. Du erkennst sicher, dass wir bei der Torsion keine Normalspannungen erhalten können. Dementsprechend betrachten wir hier Schubspannungen. Da die Torsion ein Moment in x-Richtung ist, erhalten wir aus dem Momentengleichgewicht:
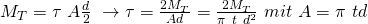
Bei der Torsion verdreht sich der Querschnitt. Demnach können wir einen Drehwinkel messen. Vom Drehwinkel können wir dann auf den Scherwinkel schließen mit
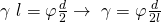
Auch hier gibt es einen linearen Bereich. Aus diesem linearen Bereich erhalten wir den formelmäßigen Zusammenhang:
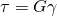
G beschreibt den sogenannten Schubmodul. Dieser Schubmodul beschreibt die Festigkeit gegenüber Schubspannungen, ist materialabhängig und wird, wie die Spannungen, in Pascal bzw. Megapascal angegeben. Du kannst dir sicher denken, dass es eine ähnliche Größe für Normalspannungen geben muss. Diese ist im sogenannten „Hook’schen Gesetz“ zu finden. Dieses gilt für alle elastisch verformbaren Körper und bedeutet, dass die Längenänderung und die einwirkende Kraft zueinander proportional sind: 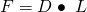 :
:
Das Hook’sche Gesetz
Das Hook’sche Gesetz wirst du bei der Betrachtung von Spannungen und Dehnung immer wieder vorfinden. Der Gültigkeitsbereich ist der lineare Bereich im Graphen des Zugversuchs, da wir einen linearen Zusammenhang zwischen Spannung und Dehnung herstellen. Der Bereich verliert deshalb an Gültigkeit, sobald wir den linearen Bereich verlassen. Aufgrund der einwirkenden Kraft auf das Material, ergibt sich zusätzlich auch eine Dehnung Epsilon:
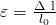
Analog zu den Schubspannungen ergibt sich dann mit der Dehnung Epsilon:
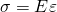
E ist der sogenannte Elastizitätsmodul oder kurz einfach E-Modul. Der E-Modul ist eine materialabhängige Größe und beschreibt die Festigkeit gegenüber Normalspannungen. Kurz gesagt gibt er an, wie stark ein Material bei Einfluss einer Kraft nachgibt. Er hat natürlich auch die Einheit Pascal bzw. Megapascal.
Im Hook’schen Gesetz finden wir noch die sogenannte Querkontraktionszahl 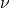 Nü. Diese resultiert aus der Überlegung, dass durch eine Längenänderung auch eine Änderung des Querschnitts entsteht und ist eine materialabhängige Größe, allerdings ohne Einheit. Das kennst du sicher auch vom Gummiband, dass immer dünner wird, je länger du es ziehst. Für ein isotropes, also in allen Stoffeigenschaften konstantes, Material gilt dann, falls wir in y-Richtung ziehen:
Nü. Diese resultiert aus der Überlegung, dass durch eine Längenänderung auch eine Änderung des Querschnitts entsteht und ist eine materialabhängige Größe, allerdings ohne Einheit. Das kennst du sicher auch vom Gummiband, dass immer dünner wird, je länger du es ziehst. Für ein isotropes, also in allen Stoffeigenschaften konstantes, Material gilt dann, falls wir in y-Richtung ziehen:
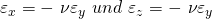
Betrachten wir jetzt die Volumenänderung, erhalten wir:
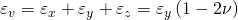
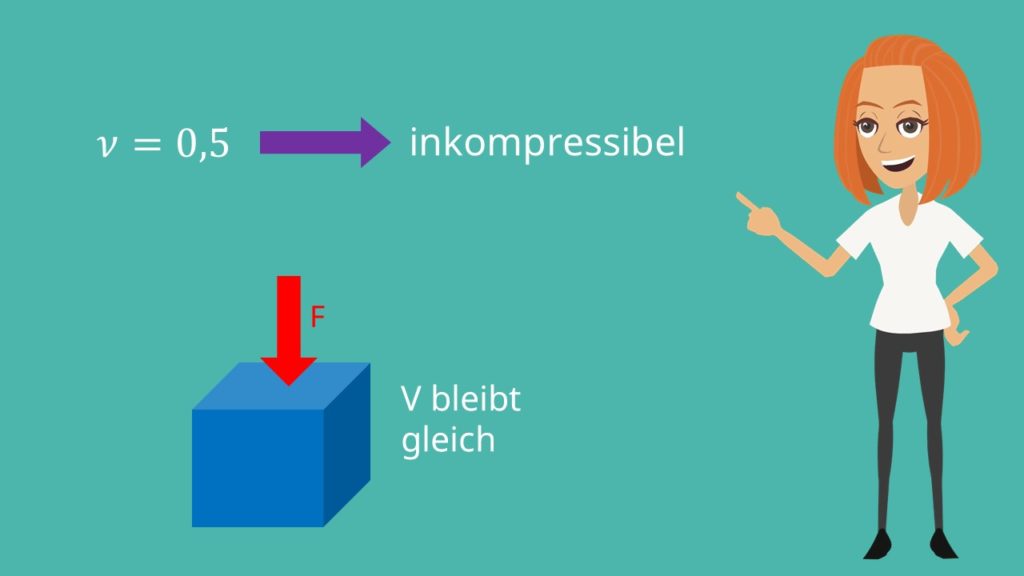
Da die herkömmlichen Werkstoffe ihr Volumen im Zugversuch nicht verringern, muss die Querkontraktionszahl kleiner als 0,5 sein. Falls die Querkontraktionszahl gleich 0,5 ist, haben wir einen vollständig inkompressiblen Werkstoff. Dies bedeutet dieser Werkstoff hat die Eigenschaft sein Volumen unter Druckeinfluss bei konstanter Temperatur nicht zu ändern.
Das Hook’sche Gesetz im dreidimensionalen Raum
Das Hook’sche Gesetzt existiert nicht nur im ebenen Fall, sondern auch in alle drei Koordinatenrichtungen. Dabei macht man den Zugversuch in jede Richtung und überlagert die Ergebnisse. Die Überlagerung und Umformung für jede Koordinatenrichtung sind jetzt vergleichsweise komplex. Dies wollen wir dir ersparen und du siehst hier nur die Formeln, mit denen du dann auch Arbeiten kannst.
Und zu den restlichen Dehnungen mit 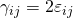 :
:
Du weißt jetzt, wo du Querkontraktionszahl, E-Modul und Schubmodul verwendest. Doch zwischen den drei Größen, gibt es auch einen einfachen Zusammenhang:
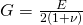
Das heißt, wenn du zwei der drei Werte kennst, kannst du dir immer den dritten Wert berechnen.
Bisher haben wir nur die Dehnung durch Krafteinwirkung betrachtet. Doch du kennst sicher auch, dass sich Materialien ausdehnen, wenn sie heiß werden. Das heißt, auch die Temperatur spielt eine Rolle. Zur Betrachtung dieses Phänomens, nehmen wir jetzt an, dass sich unser Material linear verhält. Das heißt unsere Dehnungen in Achsenrichtung 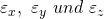 sind proportional zur Temperatur und alle anderen Dehnungen
sind proportional zur Temperatur und alle anderen Dehnungen 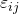 sind Null. Daraus ergibt sich für uns:
sind Null. Daraus ergibt sich für uns:
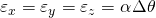
Alpha ist der sogenannte Temperaturdehnungskoeffizient und Delta Theta beschreibt die Temperaturänderung, die zur Dehnung führt.
Den Term können wir einfach zu unseren bereits bekannten Termen addieren.
Festigkeitshypothese und Fließgrenze
Doch was bringt uns das jetzt? Du weißt, dass jedes Material eine Grenze hat, an dem es bricht. Das soll aber nach Möglichkeit verhindert werden, denn dein Auto soll ja nicht während der Fahrt auseinander brechen. Dafür benötigen wir ein Maß, wie die Dehnung oder die Spannung. Da die Werte oft empirisch, also im Versuch, ermittelt werden, können wir Materialien nicht exakt bis zur Grenze belasten, sondern sollten eine Sicherheit einbauen. Deshalb gibt es sogenannte Festigkeitshypothesen. Diese ermöglichen es dir eine schnelle und einfache Abschätzung zur Bauteilfestigkeit zu treffen.
In der Regel wird als Kriterium dafür die Fließgrenze genommen. Die Fließgrenze ist der Punkt, an dem das Material dauerhaft plastisch verformt ist. Das heißt ab dem Punkt, an dem du dein Gummiband ausleierst. Hier geht dein Gummi noch nicht kaputt, verliert aber an Festigkeit.
Jetzt weißt du, dass dein Gummiband einen geringen E-Modul als andere Materialien haben muss, damit es sich so einfach langziehen lassen kann. Bis bald!