Injektiv Surjektiv Bijektiv
In diesem Beitrag und im Video erklären wir dir die Begriffe Injektivität, Surjektivität und Bijektivität. Dabei schauen wir uns wichtige Eigenschaften an und zeigen viele Beispielaufgaben mit Lösungen.
Inhaltsübersicht
Injektiv, Surjektiv, Bijektiv einfach erklärt
Die Begriffe Injektiv, Surjektiv und Bijektiv beschreiben Eigenschaften von Funktionen bzw. Abbildungen, also Abbildungseigenschaften. Eine Abbildung oder eine Funktion ist eine eindeutige Zuordnung zwischen zwei Mengen A und B.
Durch eine Abbildung f wird also jedem Element 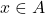 aus der der Definitionsmenge A genau ein Element
aus der der Definitionsmenge A genau ein Element 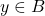 aus der Zielmenge B zugeordnet. Dieses Element y wird auch mit
aus der Zielmenge B zugeordnet. Dieses Element y wird auch mit 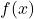 bezeichnet. Die Menge der Elemente aus B, auf die die Abbildung auch tatsächlich abbildet, wird als Bildmenge bezeichnet.
bezeichnet. Die Menge der Elemente aus B, auf die die Abbildung auch tatsächlich abbildet, wird als Bildmenge bezeichnet.
Injektiv
Die Injektivität als Eigenschaft einer Funktion beschreibt die Tatsache, dass jedes Element der Zielmenge maximal einmal als Funktionswert angenommen wird. Das bedeutet, dass keine zwei verschiedenen Elemente der Definitionsmenge auf das gleiche Element der Zielmenge abgebildet werden.
Ist eine Funktion injektiv, so wird sie auch linkseindeutig genannt und als Injektion bezeichnet. Eine linkseindeutige Funktion muss nicht per Voraussetzung auf alle Elemente in der Zielmenge abbilden. Das bedeutet, dass die Bildmenge kleiner sein kann als die Zielmenge.
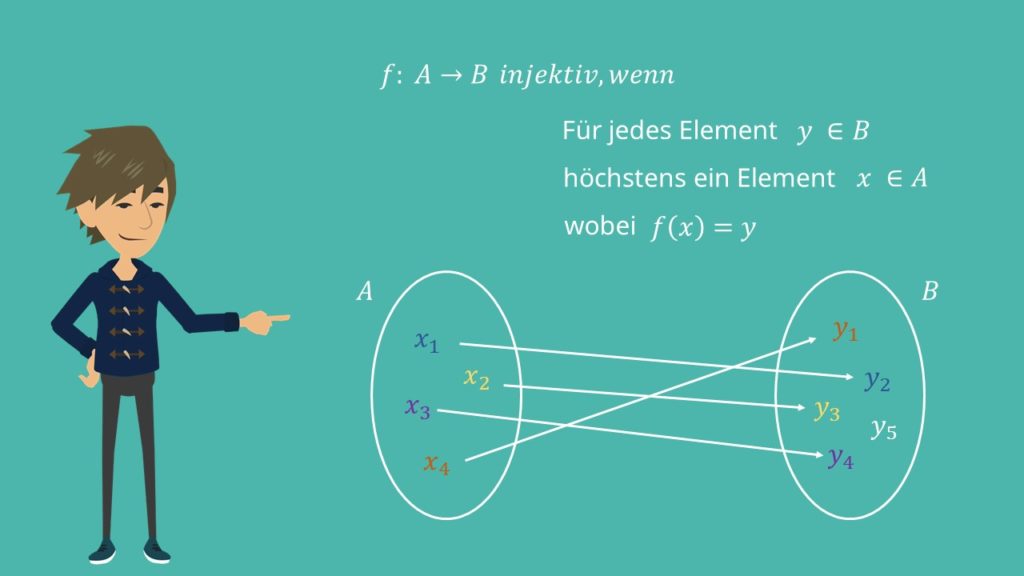
Definition Injektiv
Konkret formuliert ist eine injektive Abbildung wie folgt definiert:
Eine Abbildung 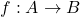 zwischen den zwei Mengen A und B heißt injektiv, wenn zu jedem
zwischen den zwei Mengen A und B heißt injektiv, wenn zu jedem 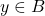 höchstens ein
höchstens ein 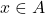 mit
mit 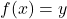 existiert.
existiert.
In formaler Schreibweise kann diese Definition auch folgendermaßen notiert werden:
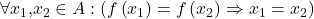
Ausgesprochen bedeutet dies: Sind die Funktionswerte einer injektiven Funktion für zwei Elemente der Definitionsmenge dieselben, so müssen die beiden Elemente bereits gleich sein.
Grafische Darstellung der Injektivität
Werden die beiden Mengen A und B mit ihren Elementen in einem Mengen-Diagramm dargestellt, so kann die Abbildung f durch Pfeile dargestellt werden, welche von Elementen aus der Definitionsmenge zu den entsprechenden Elementen in der Zielmenge laufen.
In einer solchen Darstellung wird die Injektivität der Funktion dadurch deutlich, dass auf kein Element der Zielmenge B mehr als ein Abbildungspfeil trifft.
Wird eine Funktion betrachtet, die von einem reellen Intervall in eine Teilmenge der reellen Zahlen abbildet, so kann diese Funktion durch einen herkömmlichen Funktionsgraphen veranschaulicht werden. Hierbei spiegelt sich die Injektivität in der Tatsache wider, dass jede waagrechte Gerade den Graphen einer linkseindeutigen Funktion höchstens einmal schneidet.
Beispiele: Injektive Funktionen
Die Abbildung, die einem Studenten einer Universität seine Matrikelnummer zuweist, ist eine injektive Abbildung. Es gibt nämlich keine zwei Studenten an einer Universität, die dieselbe Matrikelnummer besitzen.
-
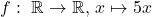 ist injektiv
ist injektiv -
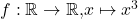 ist injektiv
ist injektiv -
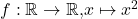 ist nicht injektiv
ist nicht injektiv -
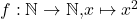 ist injektiv
ist injektiv
Eigenschaften injektiver Funktionen
- Stetige Funktionen, die von einem reellen Intervall in die reellen Zahlen abbilden sind genau dann injektiv, wenn sie auf dem ganzen Definitionsbereich streng monoton steigend oder fallend sind.
- Sind zwei Funktionen
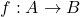 und
und 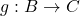 injektiv, so gilt das auch für die Komposition (Verkettung)
injektiv, so gilt das auch für die Komposition (Verkettung) 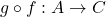
- Aus der Injektivität von
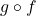 folgt die Injektivität der Abbildung
folgt die Injektivität der Abbildung 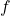
- Eine Funktion
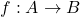 ist genau dann injektiv, wenn für alle Teilmengen
ist genau dann injektiv, wenn für alle Teilmengen 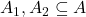 der Definitionsmenge
der Definitionsmenge 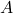 gilt:
gilt: 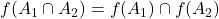
Injektivität beweisen
In vielen Aufgabenstellungen ist zu zeigen, dass eine Abbildung injektiv ist. In der Regel ist für die zu untersuchende Abbildung eine Abbildungsvorschrift angegeben. Dadurch lässt sich die Injektivität einer Funktion 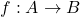 mit folgender Beweisidee zeigen.
mit folgender Beweisidee zeigen.
Zunächst wird angenommen dass die Funktionswerte 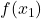 und
und 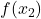 zu den Elementen
zu den Elementen 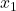 und
und 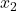 der Definitionsmenge A gleich sind:
der Definitionsmenge A gleich sind:
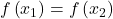
Lässt sich nun zeigen, dass daraus folgt, dass die Elemente 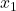 und
und 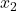 identisch sind, so ist die Funktion f injektiv.
identisch sind, so ist die Funktion f injektiv.
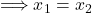
Soll gezeigt werden, dass die betrachtete Abbildung nicht injektiv ist, so genügt es zwei unterschiedliche Elemente der Definitionsmenge zu finden, welche durch die Abbildung f auf ein und dasselbe Element 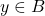 geschickt werden.
geschickt werden.
Diese Beweisidee soll nun an konkreten Beispielaufgaben durchgeführt werden.
Aufgaben mit Lösungen zur Injektivität
Zunächst soll die Funktion 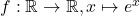 auf Injektivität überprüft werden.
auf Injektivität überprüft werden.
Hierzu wird erst einmal angenommen, dass für 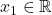 und
und 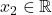 gilt:
gilt:
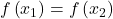
Dies bedeutet:
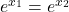
Wird auf beiden Seiten der natürliche Logarithmus angewandt ergibt sich:
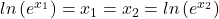
Somit wurde gezeigt, dass die Exponentialfunktion injektiv ist.
Auf dieselbe Art läuft der Beweis, dass die Funktion 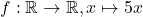 injektiv ist.
injektiv ist.
Zunächst wird wieder angenommen, dass für 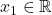 und
und 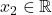 gilt:
gilt:
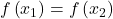
Ausgeschrieben lautet diese Annahme folgendermaßen:
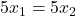
Daraus folgt direkt 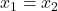 und die Injektivität der Funktion ist gezeigt.
und die Injektivität der Funktion ist gezeigt.
Surjektiv
Surjektivität einer Funktion bedeutet, dass jedes Element der Zielmenge mindestens einmal als Funktionswert angenommen wird. Das bedeutet, dass jedes Element der Zielmenge ein nicht leeres Urbild besitzt. Eine surjektive Funktion wird auch als rechtstotal bezeichnet und sie wird Surjektion genannt.
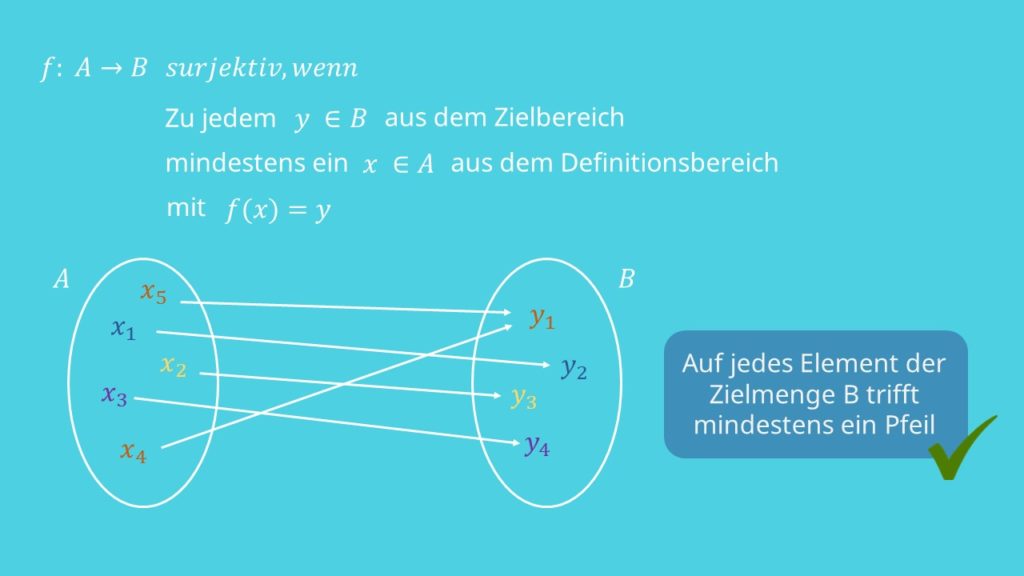
Definition Surjektiv
Eine surjektive Funktion kann wie folgt definiert werden:
Eine Abbildung 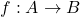 zwischen den zwei Mengen A und B heißt surjektiv, wenn zu jedem
zwischen den zwei Mengen A und B heißt surjektiv, wenn zu jedem 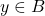 mindestens ein
mindestens ein 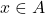 mit
mit 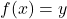 existiert.
existiert.
In formaler Schreibweise lautet die Bedingung folgendermaßen:
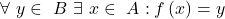
Beispiele: Surjektive Funktionen
Die Funktion, die jedem Studenten einen Geburtsmonat zuweist, ist surjektiv.
-
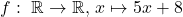 ist surjektiv
ist surjektiv -
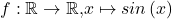 ist nicht surjektiv
ist nicht surjektiv -
![Rendered by QuickLaTeX.com f:\ \mathbb{R}\rightarrow[-1,1],x↦sin(x)](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cb95aee01cd7e99468d1d96d17f5836b_l3.png) ist surjektiv
ist surjektiv -
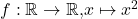 ist nicht surjektiv
ist nicht surjektiv -
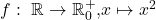 ist surjektiv
ist surjektiv
Eigenschaften surjektiver Funktionen
- Sind zwei Funktionen
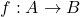 und
und 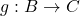 surjektiv, so gilt das auch für die Komposition (Verkettung)
surjektiv, so gilt das auch für die Komposition (Verkettung) 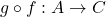
- Aus der Surjektivität von
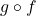 folgt die Surjektivität der Abbildung g
folgt die Surjektivität der Abbildung g
Surjektivität beweisen
Soll für eine Funktion 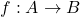 deren Surjektivität nachgewiesen werden, so bietet sich folgende Beweisstrategie an:
deren Surjektivität nachgewiesen werden, so bietet sich folgende Beweisstrategie an:
Da für jedes 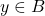 ein
ein 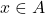 mit
mit 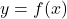 existieren muss, wird diese Gleichung erst einmal formuliert:
existieren muss, wird diese Gleichung erst einmal formuliert:
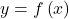
Anschließend wird diese Gleichung nach x aufgelöst und überprüft, ob der erhaltene Ausdruck für x, der von y abhängt, auch für alle 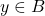 ein Element der Definitionsmenge A ist. In diesem Fall ist die Funktion surjektiv.
ein Element der Definitionsmenge A ist. In diesem Fall ist die Funktion surjektiv.
Wie diese Strategie konkret durchgeführt wird, soll an nun folgenden Beispielaufgaben gezeigt werden.
Aufgaben mit Lösungen zur Surjektivität
Als erstes soll die Surjektivität der Funktion 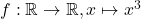 gezeigt werden.
gezeigt werden.
Dazu wird erst einmal folgende Gleichung formuliert:
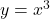
Diese wird nun nach x umgestellt. Es ergibt sich:
![Rendered by QuickLaTeX.com x=\sqrt[3]{y}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5476227871c3a9f05a922bc61a128279_l3.png)
Da ![Rendered by QuickLaTeX.com \sqrt[3]{y}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f49d30da611c50f896a33adcc11753c7_l3.png) für alle
für alle 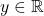 auch in
auch in 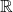 liegt, ist die Funktion somit surjektiv.
liegt, ist die Funktion somit surjektiv.
Genauso läuft der Nachweis, dass die Funktion 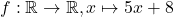 surjektiv ist.
surjektiv ist.
Zunächst wird die Gleichung 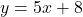 notiert, welche anschließend nach x umgestellt wird:
notiert, welche anschließend nach x umgestellt wird:
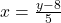
Da 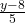 für alle
für alle 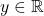 ein Element aus
ein Element aus 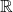 ist, ist auch die Funktion
ist, ist auch die Funktion 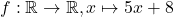 surjektiv.
surjektiv.
Bijektiv
Die Eigenschaft der Bijektivität einer Abbildung ist gegeben, wenn die Abbildung sowohl injektiv als auch surjektiv ist. Das heißt, dass sie zum einen verschiedene Elemente der Definitionsmenge auf verschiedene Elemente der Zielmenge abbildet (Injektivität) und zum anderen auch jedes Element der Zielmenge trifft (Surjektivität).
Für endliche Mengen besitzen daher die Definitionsmenge, die Bildmenge und die Zielmenge einer bijektiven Abbildung gleich viele Elemente. Umgekehrt ist eine Abbildung bijektiv, sobald die Anzahlen dieser drei Mengen übereinstimmen.
Eine bijektive Abbildung wird auch als Bijektion bezeichnet und sie besitzt stets eine Umkehrabbildung. Sie ist also invertierbar.
Definition Bijektiv
Eine Abbildung ist bijektiv, wenn sie sowohl injektiv als auch surjektiv ist.
Die Abbildung f: A → B zwischen den zwei Mengen A und B ist also bijektiv, wenn zu jedem y ∈ B genau ein x ∈ A mit f(x) = y existiert.
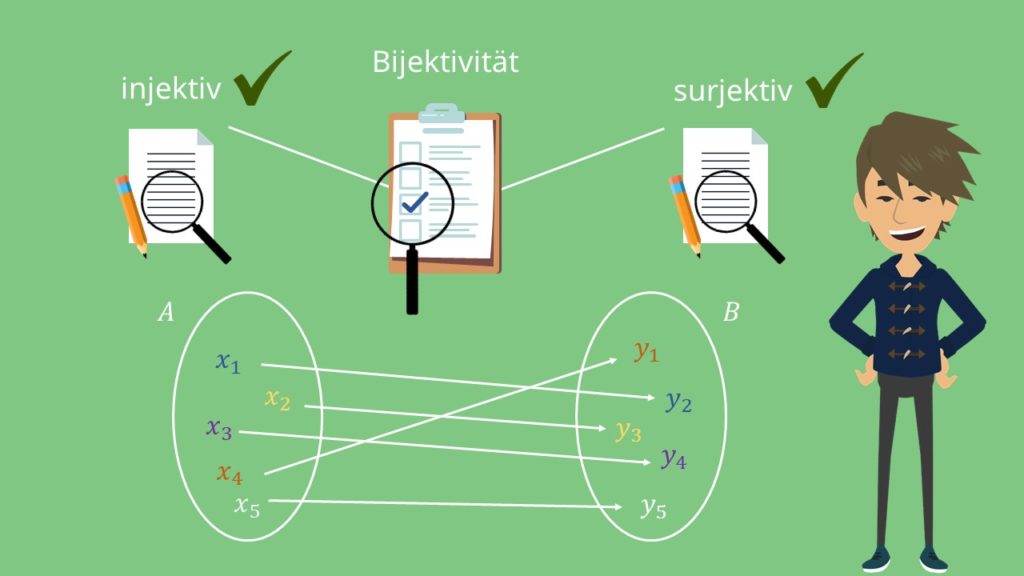
Grafische Darstellung der Bijektivität
Wird eine Bijektion in einem Mengendiagramm dargestellt, sieht das wie folgt aus:
In einer solchen Darstellung einer bijektiven Abbildung, muss von jedem Element aus A genau ein Abbildungspfeil ausgehen und auf jedes Element aus B muss wiederum genau ein Abbildungspfeil auftreffen.
Beispiele: Bijektive Funktionen
Wird jedem monogam verheiratetem Menschen sein Ehepartner bzw. seine Ehepartnerin zugeordnet, so stellt dies eine Bijektion zwischen allen verheirateten Menschen dar.
-
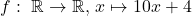 ist bijektiv mit der Umkehrabbildung
ist bijektiv mit der Umkehrabbildung 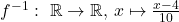
-
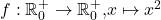 ist bijektiv
ist bijektiv -
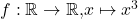 ist bijektiv
ist bijektiv
Eigenschaften bijektiver Funktionen
Seien A und B endliche Mengen, die gleich viele Elemente enthalten. Dann gilt für die Abbildung 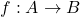 :
:
- Ist
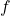 injektiv, so ist
injektiv, so ist 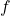 auch surjektiv und somit bijektiv
auch surjektiv und somit bijektiv - Ist
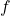 surjektiv, so ist
surjektiv, so ist 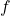 auch injektiv und somit bijektiv
auch injektiv und somit bijektiv
Sind zwei Funktionen 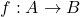 und
und 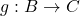 bijektiv, so ist auch die Komposition (Verkettung)
bijektiv, so ist auch die Komposition (Verkettung) 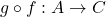 bijektiv. Die Umkehrfunktion lautet in diesem Fall
bijektiv. Die Umkehrfunktion lautet in diesem Fall 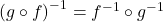 .
.
Ist 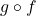 bijektiv, so ist
bijektiv, so ist 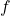 injektiv und
injektiv und 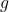 surjektiv
surjektiv
Bijektivität beweisen
Aufgrund der Definition der Bijektivität ist offensichtlich, wie gezeigt werden kann, dass eine Abbildung bijektiv ist. Für diese Abbildung muss sowohl die Injektivität als auch die Surjektivität nachgewiesen werden.
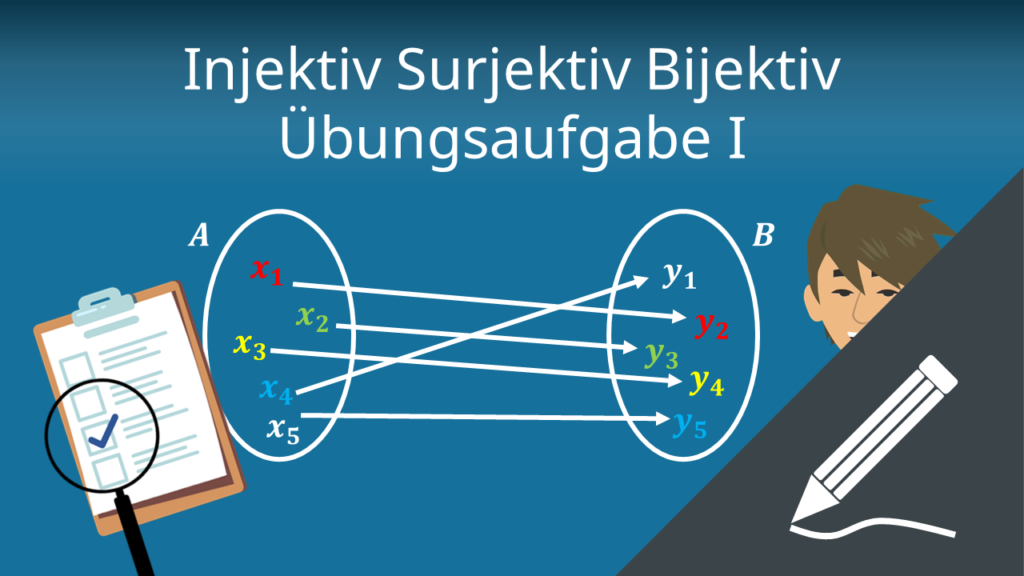
Injektiv Surjektiv Bijektiv Übungsaufgabe I
Betrachten wir nun eine Übungsaufgabe, um dir das Thema näherzubringen.
Entscheide, ob die folgende Abbildung injektiv, surjektiv, oder bijektiv ist. Begründe deine Antwort.
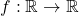
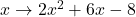
Wie du siehst bildet die betrachtete Funktion die reellen Zahlen wieder auf die reellen Zahlen ab. Das heißt, es lässt sich ein Funktionsgraph zu der Funktion zeichnen. Bei der Lösung der Aufgabe kann es dir helfen, dir zu überlegen wie in etwa dieser Funktionsgraph aussieht.
Die Lösung zu dieser Aufgabe mit einer verständlichen Erklärung findest du in unserem zugehörigen Video .
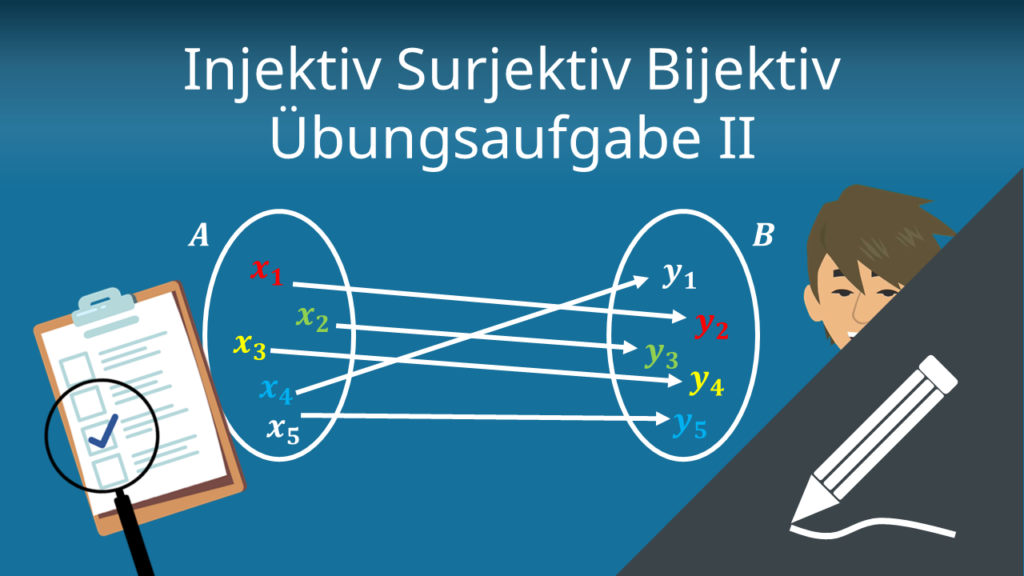
Injektiv Surjektiv Bijektiv Übungsaufgabe II
Die folgende Aufgabe um die Abbildungseigenschaften zu bestimmen ist etwas komplexer.
Entscheide ob die folgende Funktion injektiv, surjektiv oder bijektiv ist. Begründe deine Antwort.
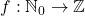
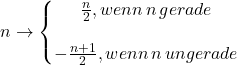
Bei der Lösung der Aufgabe ist es wichtig, dass du dir erst einmal bewusst machst, wie die Definitionsmenge und die Zielmenge aussehen.
In unserem Video erklären wir dir Schritt für Schritt, wie du diese Aufgabe bearbeiten kannst.