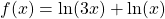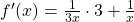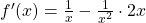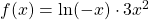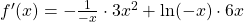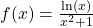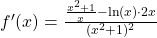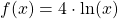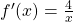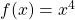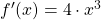ln ableiten
In diesem Artikel lernst du die Ableitung vom ln kennen. Du möchtest ohne große Anstrengung verstehen, wie du den ln x ableiten kannst? Dann schau dir unser Video dazu an!
Inhaltsübersicht
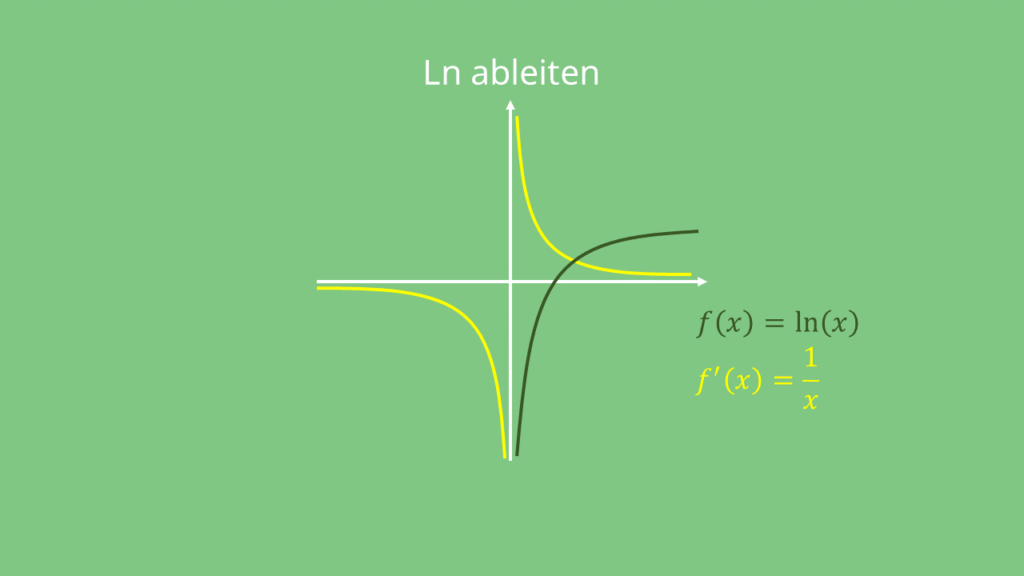
Ableitung ln einfach erklärt
Die Ableitung vom ln x (natürlicher Logarithmus) kannst du dir ganz leicht merken:
![Rendered by QuickLaTeX.com \[f(x)=\ln(\textcolor{blue}{x}) \quad \rightarrow \quad f'(x)=\frac{1}{\textcolor{blue}{x}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9c1b118341200cb58a33862c7d50b2fd_l3.png)
Für die Ableitung der meisten Funktionen mit ln brauchst du die Kettenregel . Dazu teilst du zum Beispiel die Funktion
f(x)= ln(3x + 1)
in eine innere Funktion v = 3x + 1 und eine äußere Funktion u = ln. Du leitest die innere Funktion ab, also v‘ = 3. Die Ableitung vom ln ist dann:
f'(x) = 1/(3x+1) • 3
Allgemein kannst du dir merken:
![Rendered by QuickLaTeX.com \[f(x)=\ln(\textcolor{blue}{\text{innere Funktion}})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d1de1b3dd178a1ce03e791dae3a4c639_l3.png)
![Rendered by QuickLaTeX.com \[\rightarrow \quad f'(x)=\frac{1}{\textcolor{blue}{\text{innere Funktion}}} \cdot \textcolor{red}{\text{Ableitung innere Funktion}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a9360763b291f97b3b5796350b3e16fe_l3.png)
Prima! Schau dir gleich an Beispielen an, wie du die Logarithmusfunktion ableiten kannst!
Logarithmus ableiten – Beispiel 1
Du möchtest folgende Funktion ableiten:
f(x) = ln(2x2 + 3)
Dafür bestimmst du zuerst die innere Funktion h(x) und Ableitung h'(x):
h(x) = 2x2 + 3 → h'(x) = 4x
Dabei kannst du die Potenz- und Faktorregel als Ableitungsregeln für den ln verwenden, um die Ableitung zu bestimmen.
Jetzt bildest du mithilfe der Kettenregel die gesamte Ableitung vom ln:
![Rendered by QuickLaTeX.com \[\frac{1}{\textcolor{blue}{2x^2+3}} \cdot \textcolor{red}{4x} =\frac{4x}{2x^2+3}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-82dddc2bc40976c7d1ef75a8ebbb36d7_l3.png)
Logarithmus ableiten – Beispiel 2
Schau dir noch ein weiteres Ableitung Logarithmus Beispiel an:
f(x) = 5 • ln(x2 + x)
Dafür bestimmst du wieder mit der Potenz- und Faktorregel die innere Funktion und ihre Ableitung:
h(x) = x2 + x → h'(x) = 2x + 1
Die Kettenregel als Ableitungsregel für den ln liefert dir dann als Ergebnis:
![Rendered by QuickLaTeX.com \[f'(x)= \frac{5}{\textcolor{blue}{x^2+x}} \cdot (\textcolor{red}{2x+1}) =\frac{5\cdot (2x+1)}{x^2+x}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-655aa99e321da8fd603e15b063bb9a4b_l3.png)
Logarithmus ableiten – Beispiel 3
Schau dir noch ein Beispiel zur Ableitung vom Log an:
![Rendered by QuickLaTeX.com \[f(x)=\frac{\ln(4x+2)}{3}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-48bdaa598c3a05fedb571d87e3cb62d6_l3.png)
In diesem Beispiel zum ln(x) Ableiten erhältst du als innere Funktion und deren Ableitung:
h(x) = 4x + 2 → h'(x) = 4
Damit gilt aufgrund der Kettenregel:
![Rendered by QuickLaTeX.com \[f'(x)=\frac{\frac{1}{\textcolor{blue}{4x+2}}\cdot \textcolor{red}{4}}{3} = \frac{4}{12x+6}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-52fcf9e5e3ed16f024d4263c3ba3bbd9_l3.png)
ln Funktion ableiten: Weitere Beispiele
Du weißt jetzt, wie du mit der Kettenregel und der Potenz- und Faktorregel den log ableiten kannst. Aber es kann auch vorkommen, dass du neben dieser noch weitere Ableitungsregeln anwenden musst. Es folgen nun verschiedene Regeln mit Beispielen zur Ableitung der Log Funktion:
| Ableitungsregel ln | Funktion | Ableitung |
| Summenregel |
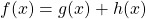
|
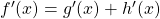
|
| Differenzregel |
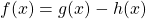
|
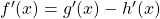
|
| Produktregel |
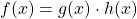
|
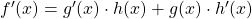
|
| Quotientenregel |
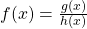
|
![Rendered by QuickLaTeX.com f'(x)=\frac{g'(x)\cdot h(x)-g(x)\cdot h'(x)}{[h(x)]^2}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e93e6ea9a3972c9e146fd256f17c1885_l3.png)
|
| Faktorregel |
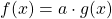
|
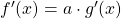
|
| Potenzregel |
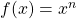
|
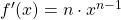
|
Weitere Funktionen und ihre Ableitungen
Du solltest nicht nur den log ableiten können, sondern auch die Ableitungen der folgenden Funktionen auswendig wissen und anwenden können:
| Funktion | Ableitung | |
| Wurzel ableiten | 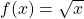 |
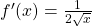 |
| Ableitung Cosinus | 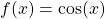 |
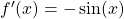 |
| Ableitung Sinus | 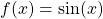 |
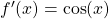 |
| Ableitung Tangens | 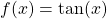 |
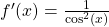 |
| e Funktion ableiten | 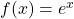 |
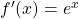 |