Umkehrfunktion
Du fragst dich, wie du Umkehrfunktionen bilden und ihre Graphen zeichnen kannst? Dann bist du bei unserem Beitrag und Video genau richtig! Hier erfährst du alles, was du wissen musst!
Inhaltsübersicht
Umkehrfunktion einfach erklärt
Du weißt, dass eine Funktion f(x) einem x-Wert einen y-Wert zuordnet. Die Umkehrfunktion f-1(x) ordnet dagegen dem y-Wert wieder den x-Wert umgekehrt zu. Das heißt, dass du die x-Werte und y-Werte deiner Funktion vertauschst. Du kannst eine Funktion nur umkehren, wenn sie jeden y-Wert höchstens einmal annimmt.
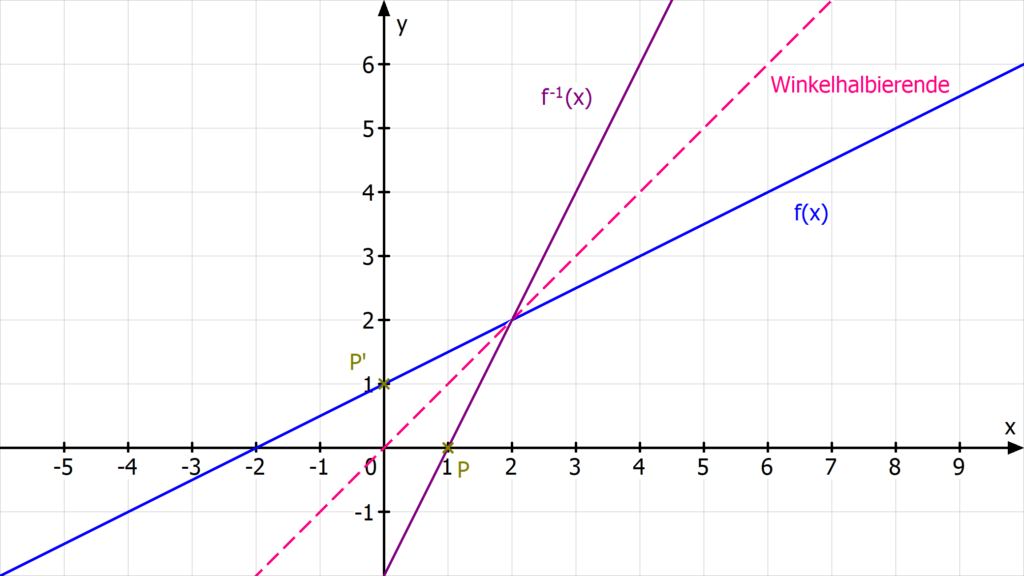
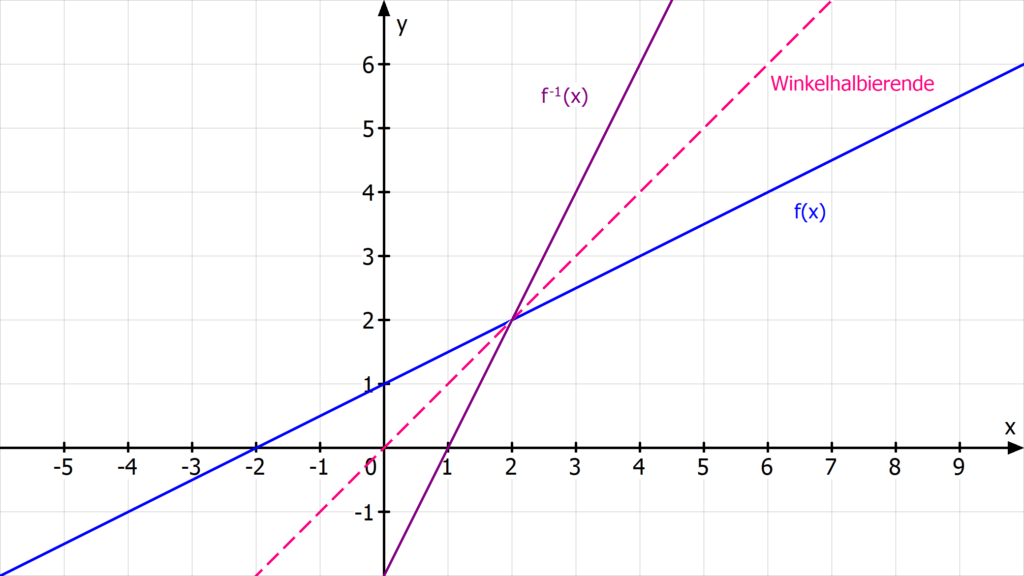
Grafisch kannst du die Umkehrfunktion immer zeichnen, indem du die Funktion f(x) an der Winkelhalbierenden (g(x) = x) spiegelst:
Geht f(x) zum Beispiel durch den Punkt P (0|1), dann vertauschst du x und y und erhältst den gespiegelten Punkt P'(1|0). Dieser geht durch den Graphen der Umkehrfunktion f-1(x).
Weil du die x- und y-Werte vertauschst, ist der Definitionsbereich von f(x) der Wertebereich deiner Umkehrabbildung f-1(x). Das Gleiche gilt für den Wertebereich von f. Der wird zum Definitionsbereich von f-1(x).
Umkehrfunktion Aufgaben
Schauen dir nun an, wie du die Umkehrfunktion berechnen kannst.
Umkehrfunktion bestimmen – lineare Funktion
Verwende direkt die lineare Funktion f(x) = 0,5x + 1. Um die Umkehrabbildung zu bestimmen, kannst du dich immer an diese Anleitung halten:
- Schritt 1: Funktionsgleichung nach x auflösen
- Schritt 2: Die Variablen x und y vertauschen
Im ersten Schritt löst du die Gleichung nach x auf. Dazu schreibst du statt f(x) einfach y.
y = 0,5x + 1 | – 1
y – 1 = 0,5x | • 2
2y – 2 = x
Jetzt musst du nur noch x und y vertauschen.
2x – 2 = y
y = 2x – 2
Die Funktion f(x) = 0,5x + 1 hat also die Umkehrabbildung f-1(x) = 2x -2.
Umkehrfunktion bestimmen – quadratische Funktion
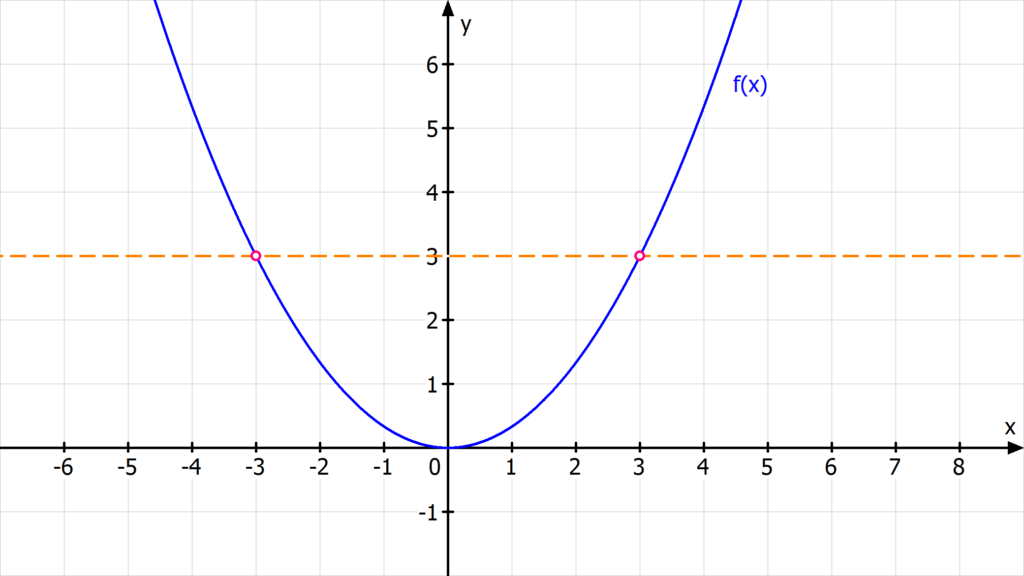
Etwas komplizierter als bei den linearen Funktionen ist die Umkehrfunktion bei quadratischen Funktionen . Das liegt im Allgemeinen daran, dass hier für einen y-Wert immer zwei x-Werte infrage kommen. Das siehst du direkt an der waagerechten Geraden:
Hier siehst du, dass die orange Gerade den Graphen der Funktion 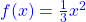 in zwei Punkten schneidet. Um die Umkehrabbildung zu bestimmen, musst du daher den Definitionsbereich
einschränken, also nur einen Teil der Funktion betrachten. In diesem Fall ist das am einfachsten, wenn du f(x) nur für positive x-Werte betrachtest.
in zwei Punkten schneidet. Um die Umkehrabbildung zu bestimmen, musst du daher den Definitionsbereich
einschränken, also nur einen Teil der Funktion betrachten. In diesem Fall ist das am einfachsten, wenn du f(x) nur für positive x-Werte betrachtest.
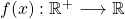
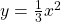
Jetzt kannst du die Umkehrabbildung berechnen, indem du nach x auflöst.
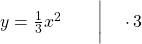

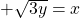
Weil du hier nur positive x-Werte betrachtest, kannst du bei der Wurzel auch nur positive Werte herausbekommen. Nun musst du nur noch x und y vertauschen und erhältst  .
.
Umkehrfunktion bestimmen – ganzrationale Funktion
Betrachte jetzt die ganzrationale Funktion f(x) = x3 – 1.
Löse die Gleichung im ersten Schritt nach x auf.
y = x3 – 1 | + 1
y + 1 = x3 | ![Rendered by QuickLaTeX.com \sqrt[3]{}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0c15c0f1433a8d72eb10e40a72d757ff_l3.png)
![Rendered by QuickLaTeX.com \sqrt[3]{y + 1}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4a01a854439c6c6323f2be1a7315a9cd_l3.png) = x
= x
Jetzt kannst du x und y vertauschen.
y = ![Rendered by QuickLaTeX.com \sqrt[3]{x+1}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-39578c2a362a3e6504eafa14b3165491_l3.png)
Die Umkehrfunktion von f(x) = x3 – 1 ist f-1(x) = ![Rendered by QuickLaTeX.com \textcolor{violet}{\sqrt[3]{x+1}}](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-cb7026442c5560ad3b2fe85013b08b73_l3.png)
Umkehrfunktion bestimmen – ex
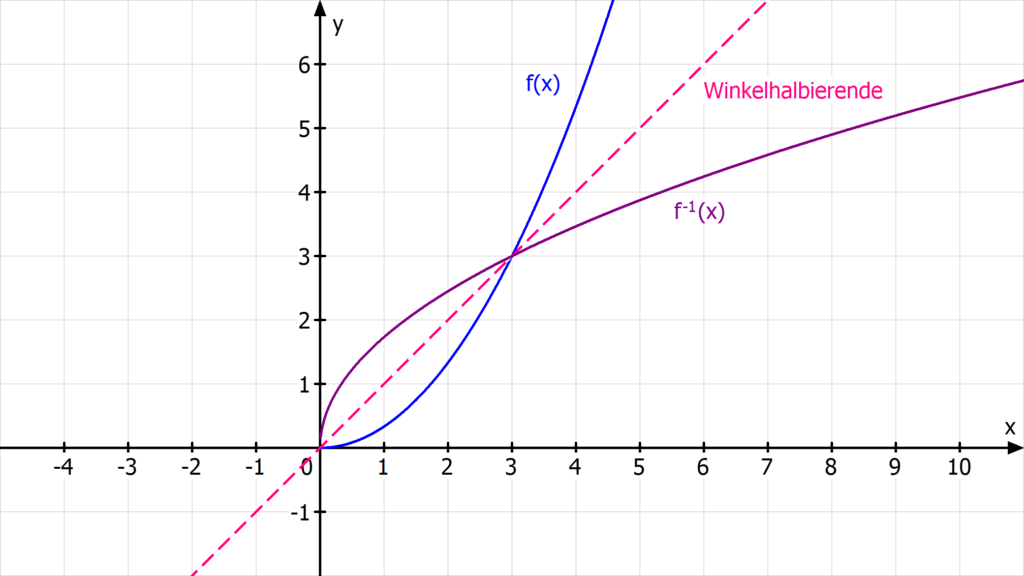
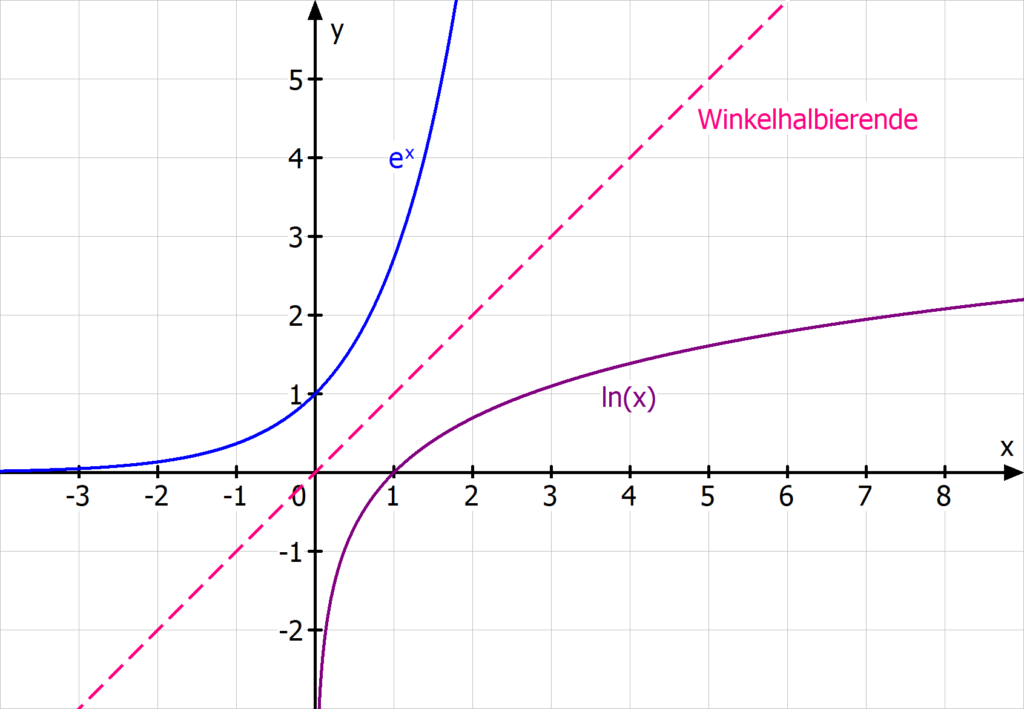
Für die e-Funktion f(x) = ex musst du die Umkehrabbildung überhaupt nicht berechnen! Hier hast du sie direkt durch die ln-Funktion f-1(x) = ln(x) gegeben. Das kommt daher, weil ln(x) als natürlicher Logarithmus zur Basis e definiert ist.
Für den Definitionsbereich und die Wertemenge der beiden Funktionen gilt dann:
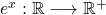
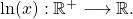
Das siehst du auch direkt an den Funktionsgraphen:
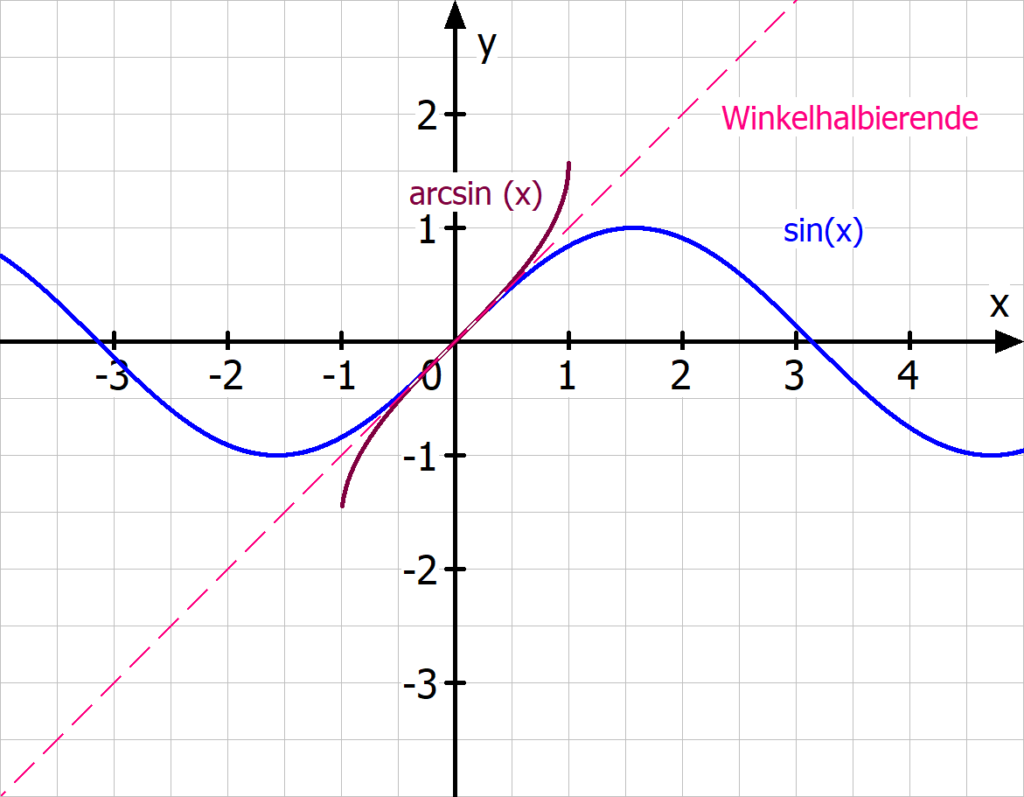
Umkehrfunktion bestimmen – Sinus
Willst du die Umkehrabbildung der Sinusfunktion bestimmen, musst du wieder nach x auflösen.
f(x) = sin(x)
Leider hilft dir da keine der vier Grundrechenarten weiter. Du brauchst den sin-1 ( ) um nach x aufzulösen. Du nennst ihn auch den Arcussinus. Ihn findest du auf deinem Taschenrechner:
y = sin(x) | sin-1 ( )
sin-1 (y) = x
Jetzt musst du nur noch x und y vertauschen:
sin-1 (x) = y
Das ist dann schon die Umkehrabbildung des Sinus.
f-1 (x) = sin-1 (x)
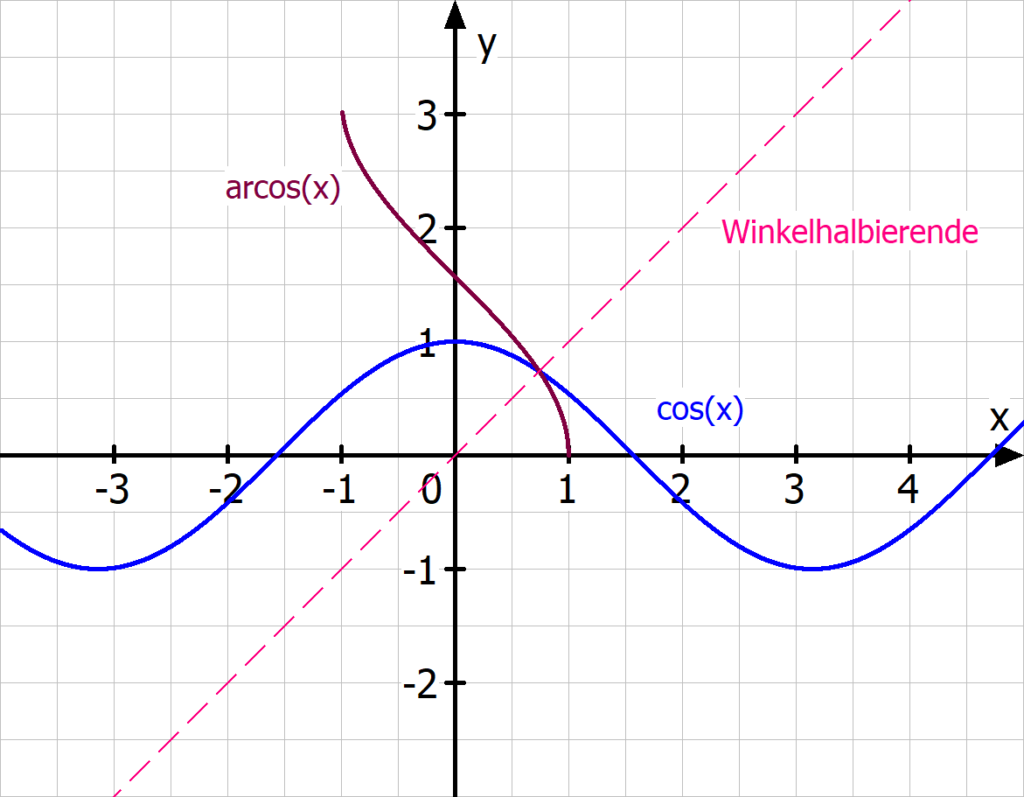
Umkehrfunktion bestimmen – Cosinus
Das Gleiche machst du auch beim Cosinus.
f(x) = cos(x)
Zuerst brauchst du für den ersten Schritt den cos-1 ( ). Das ist der Arcuscosinus. Mit ihm kannst du wie beim Sinus nach x auflösen:
y = cos(x) | cos-1 ( )
cos-1 (y) = x
Dann tauschst du wieder x und y und erhältst dann die Umkehrfunktion des Cosinus:
cos-1 (x) = y
f-1 (x) = cos-1 (x)
Ableitung der Umkehrfunktion
Für die Ableitung der Umkehrfunktion gibt es eine Abkürzung:
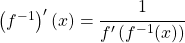
Wir haben bereits die Umkehrabbildung 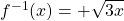 zur Funktion
zur Funktion 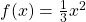 berechnet. Leitest du diese mit den bekannten Ableitungsregeln
ab, dann erhältst du:
berechnet. Leitest du diese mit den bekannten Ableitungsregeln
ab, dann erhältst du:
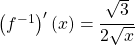 .
.
Dasselbe Ergebnis erhältst du, wenn du 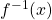 und
und 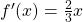 in die Formel von oben einsetzt.
in die Formel von oben einsetzt.
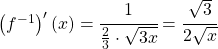
Arcustangens
Du kannst auch trigonometrische Funktionen umkehren. So ist der Arcustangens zum Beispiel die Umkehrabbildung des Tangens. Wenn du wissen willst, was es damit genau auf sich hat, dann schau dir unbedingt unser Video dazu an!