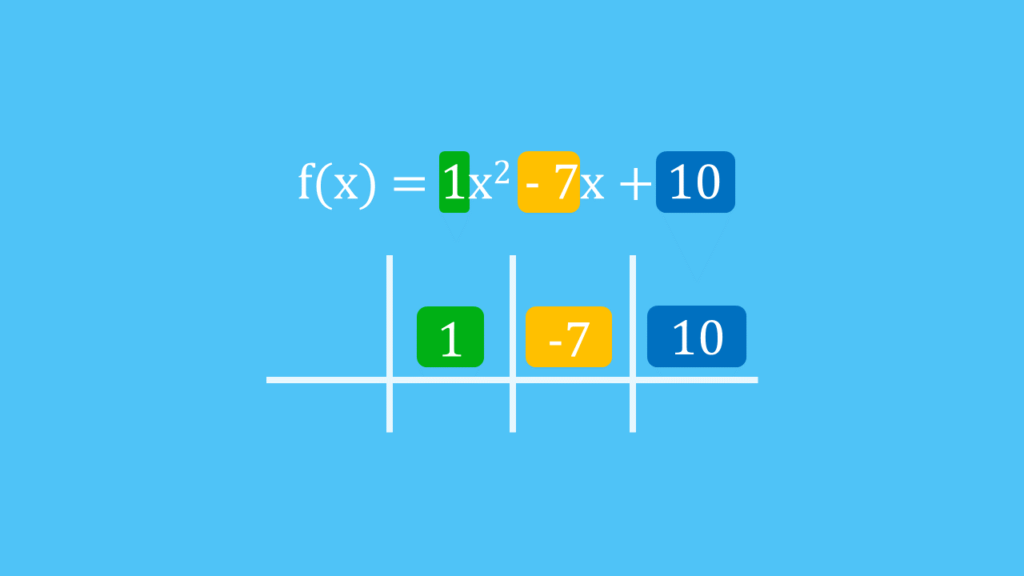Horner Schema
Das Horner Schema vereinfacht die Polynomdivision. Wie das funktioniert, erfährst du im Beitrag und in unserem Video an einem ausführlichen Beispiel.
Inhaltsübersicht
Horner Schema Beispiel
Möchtest du zwei Polynome wie 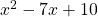 und
und  durcheinander teilen, dann kannst du dafür entweder die Polynomdivision
verwenden oder das Horner Schema. Mit dem Horner Schema kommst du durch diese vier Schritte zum Ergebnis:
durcheinander teilen, dann kannst du dafür entweder die Polynomdivision
verwenden oder das Horner Schema. Mit dem Horner Schema kommst du durch diese vier Schritte zum Ergebnis:
- Tabelle erstellen.
- Gegebene Werte eintragen.
- Restliche Tabelle nach dem Lösungsschema ausfüllen.
- Das Ergebnis der Polynomdivision aufschreiben.
Das Horner Schema lässt sich nur anwenden, wenn durch ein Polynom der Form 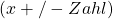 geteilt wird, also etwa
geteilt wird, also etwa 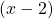 oder
oder 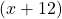 .
.
Am schnellsten verstehst du das Verfahren durch ein Beispiel. Für die Rechnung 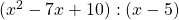 zeigen wir dir Schritt für Schritt, wie du zur Lösung kommst:
zeigen wir dir Schritt für Schritt, wie du zur Lösung kommst:
Horner Schema Schritt für Schritt
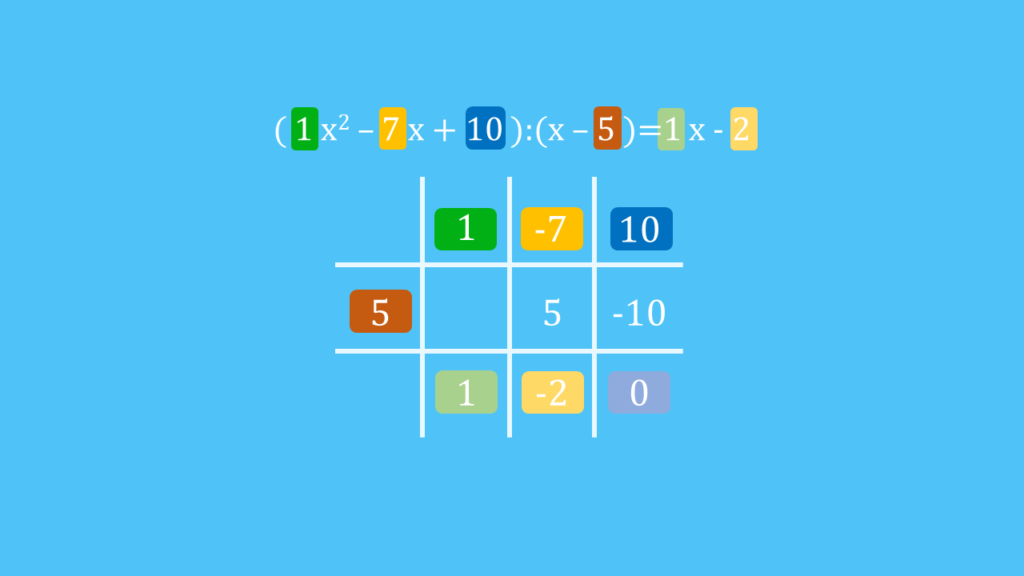
Wir wollen diese Polynomdivision mit dem Horner Schema berechnen:
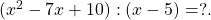
Schritt 1 – Tabelle erstellen
Die Tabelle hat immer drei Zeilen. Die Anzahl der Spalten erhältst du, indem du den Grad des Polynoms nimmst und 2 addierst. Da wir es mit einem Polynom zweiten Grades zu tun haben (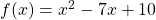 ), benötigen wir also 4 Spalten. Das Feld der ersten Zeile und ersten Spalte bleibt immer leer. Du kannst es gleich durchstreichen.
), benötigen wir also 4 Spalten. Das Feld der ersten Zeile und ersten Spalte bleibt immer leer. Du kannst es gleich durchstreichen.
Schritt 2 – Gegebene Werte eintragen
Die erste Zeile (beginnend bei der zweiten Spalte) füllst du nacheinander mit den Koeffizienten des ersten Polynoms aus. Die Koeffizienten für unser Beispiel sind 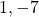 und
und 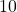 .
.
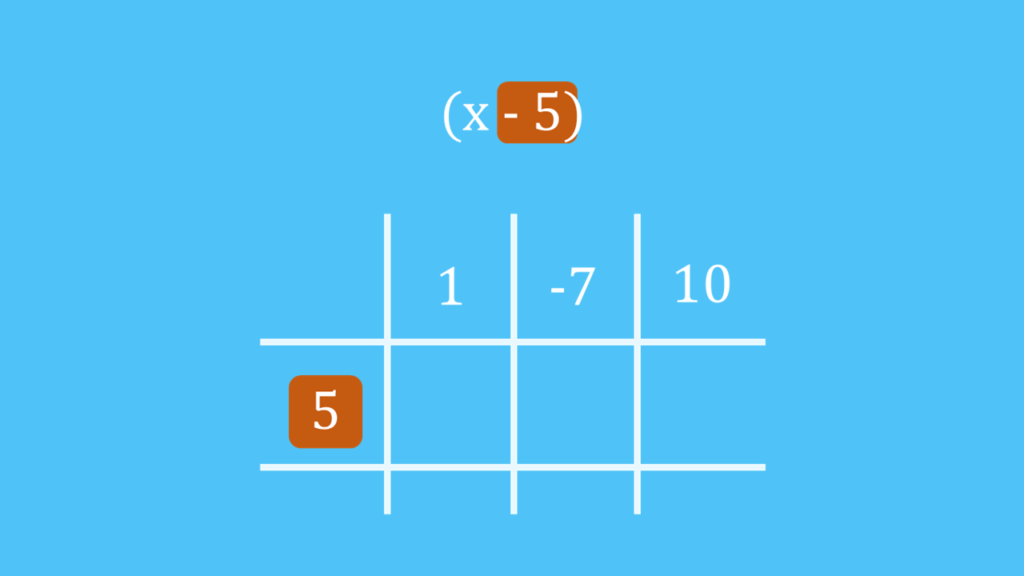
In die erste Spalte der zweiten Zeile schreibst du die Zahl beim Divisor – also dem Polynom direkt links neben dem Gleichheitszeichen – mit geändertem Vorzeichen: Der Divisor lautet 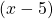 . Du nimmst also die
. Du nimmst also die 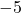 , drehst das Vorzeichen um und schreibst eine
, drehst das Vorzeichen um und schreibst eine 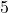 in die Tabelle.
in die Tabelle.
Damit das Horner Schema funktioniert, müssen die Polynome geordnet sein. Die einzelnen Glieder der Polynome müssen also in absteigender Reihenfolge ihrer Exponenten angeordnet sein.
Schritt 3 bis 5: Tabelle nach dem Horner Schema ausfüllen
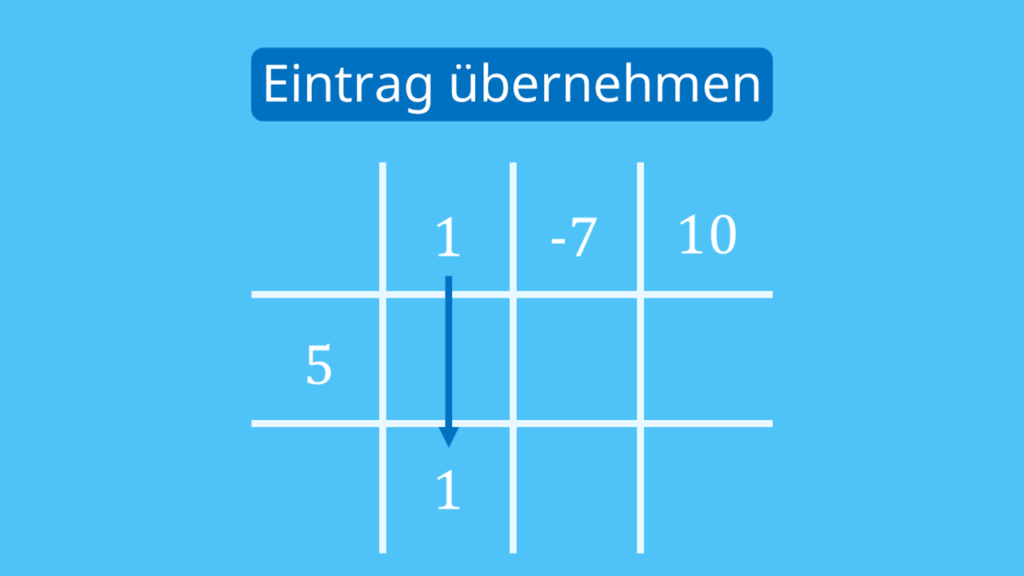
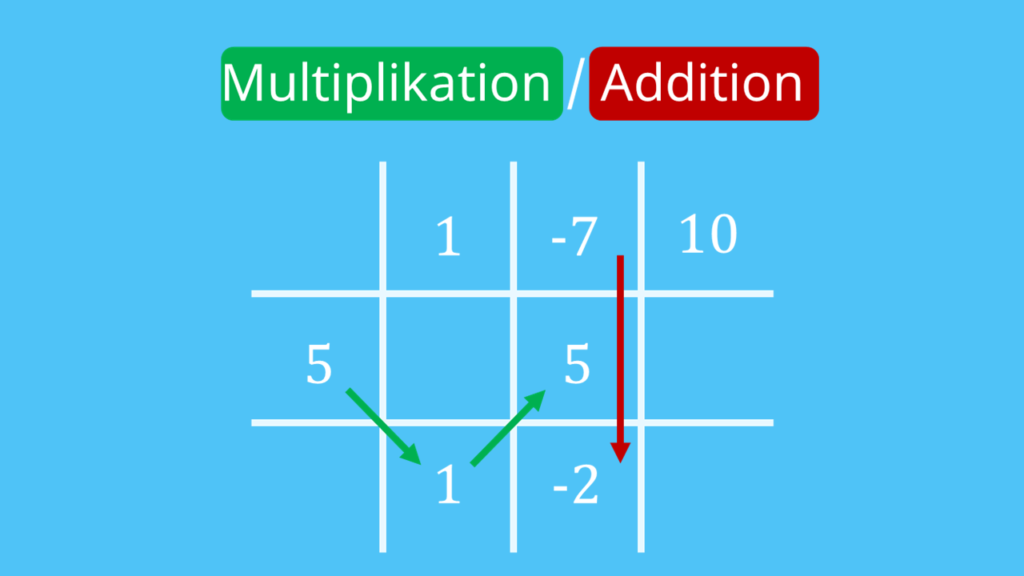
Schritt 3:
Jetzt nimmst du den ersten Eintrag der ersten Zeile und ziehst ihn direkt runter in die letzte Zeile.
Schritt 4:
Diese 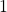 multiplizierst du anschließend mit der
multiplizierst du anschließend mit der 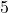 aus der ersten Spalte und schreibst das Ergebnis in die zweite Zeile unter den zweiten Koeffizienten. Unter der
aus der ersten Spalte und schreibst das Ergebnis in die zweite Zeile unter den zweiten Koeffizienten. Unter der 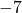 muss also eine
muss also eine 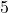 (
( ) stehen.
) stehen.
Zuletzt addierst du die beiden Zahlen in der Spalte für den zweiten Koeffizienten und schreibst das Ergebnis darunter: 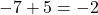
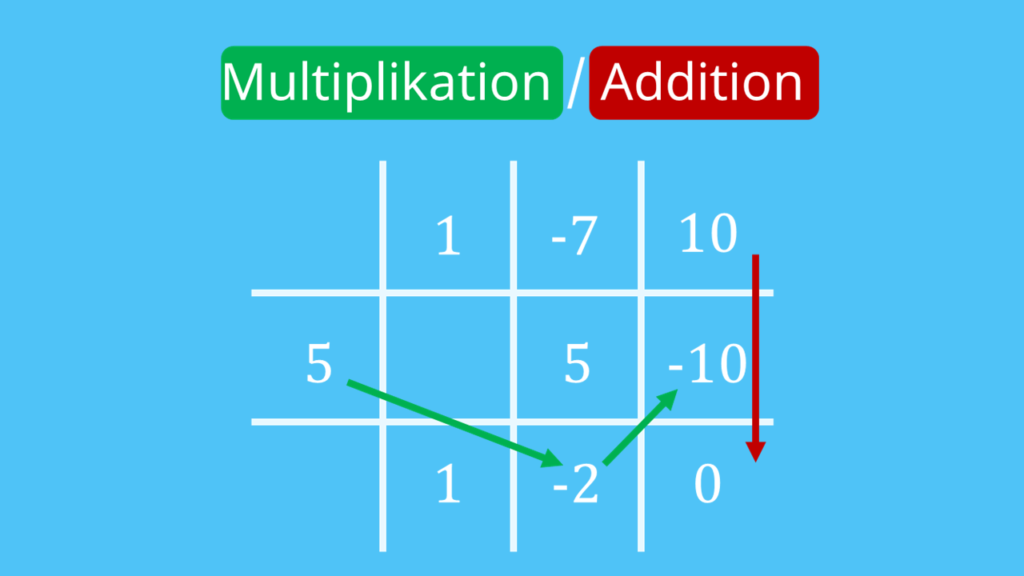
Schritt 5 bis …:
Nun wiederholst du diesen Prozess der Multiplikation und Addition. Das heißt, du multiplizierst die -2 aus der dritten Zeile mit 5 und fügst das Ergebnis in die zweite Zeile der letzten Spalte ein. Dieses Ergebnis addierst du dann mit der Zahl direkt darüber, also die 10, und fügst das Ergebnis dieser Addition direkt darunter ein.
Da du als Dividend (also das erste Polynom) ein Polynom zweiten Grades hast, bist du bereits fast fertig. Bei Polynomen höheren Grades müsstest du die Schritte hier mehrmals wiederholen.
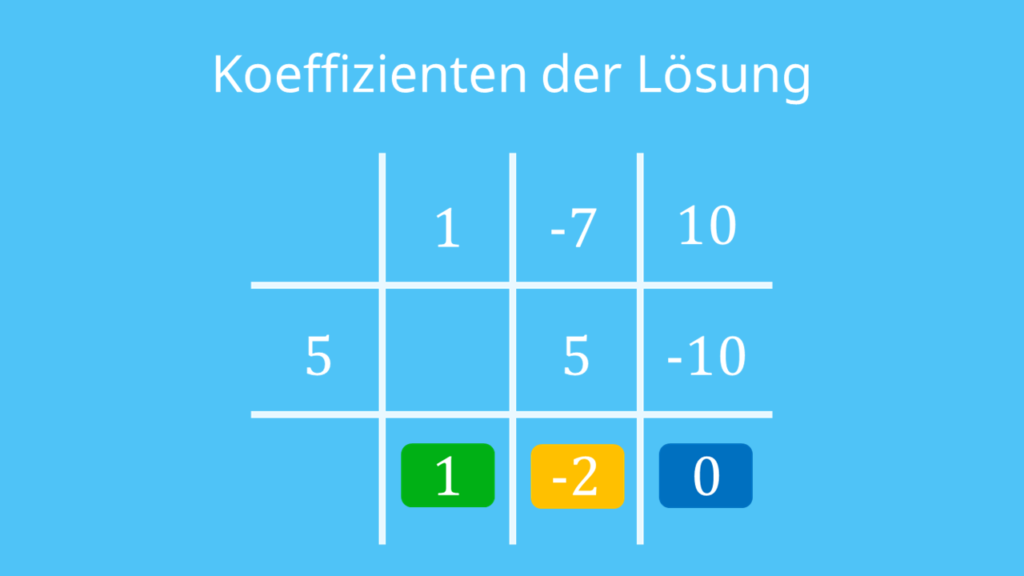
Letzter Schritt – Ergebnis ablesen und aufschreiben
In der letzten Zeile stehen nun die Koeffizienten der Lösung. Da du durch ein Polynom ersten Grades geteilt hast ( ), musst du den Grad des Lösungspolynoms um 1 reduzieren.
), musst du den Grad des Lösungspolynoms um 1 reduzieren.
Du erhältst also 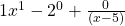 . Das letzte Glied der Lösung entspricht dem Rest der Division. Da der Koeffizient gleich Null ist, können wir ihn weglassen und erhalten:
. Das letzte Glied der Lösung entspricht dem Rest der Division. Da der Koeffizient gleich Null ist, können wir ihn weglassen und erhalten:
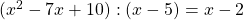
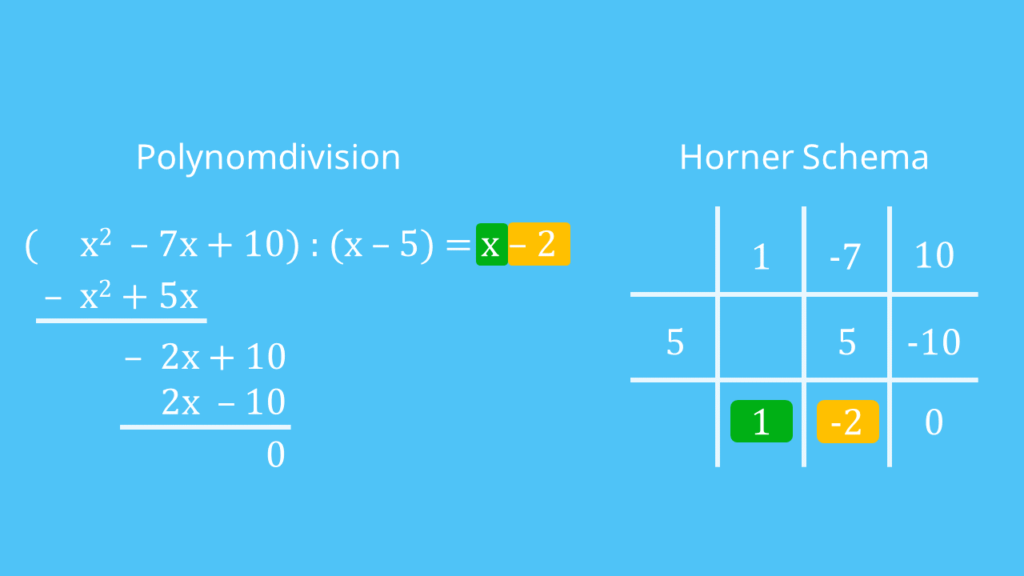
Vergleich Polynomdivision und Horner Schema
Ob du das Horner Schema verwendest oder die Polynomdivision
, bleibt dir überlassen. Du kommst mit beiden Verfahren zum selben Ergebnis. Wie die Berechnung von 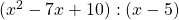 in beiden Fällen aussieht, kannst du hier vergleichen:
in beiden Fällen aussieht, kannst du hier vergleichen:
Horner Schema mit Rest
Das erste Beispiel war eine Polynomdivision ohne Rest. Was aber passiert, wenn es zu einem Rest kommt? Schauen wir uns auch dazu ein Beispiel an. Wir haben das Polynom
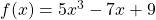
gegeben und möchten es durch
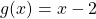
dividieren.
Der Ablauf hierfür ist identisch zum vorherigen. Du musst aber hier eine Kleinigkeit beachten: 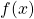 ist ein Polynom dritten Grades, aber der Term mit
ist ein Polynom dritten Grades, aber der Term mit 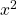 fehlt, da sein Koeffizient gleich Null ist. Du kannst
fehlt, da sein Koeffizient gleich Null ist. Du kannst 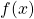 also auch so schreiben
also auch so schreiben
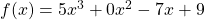 .
.
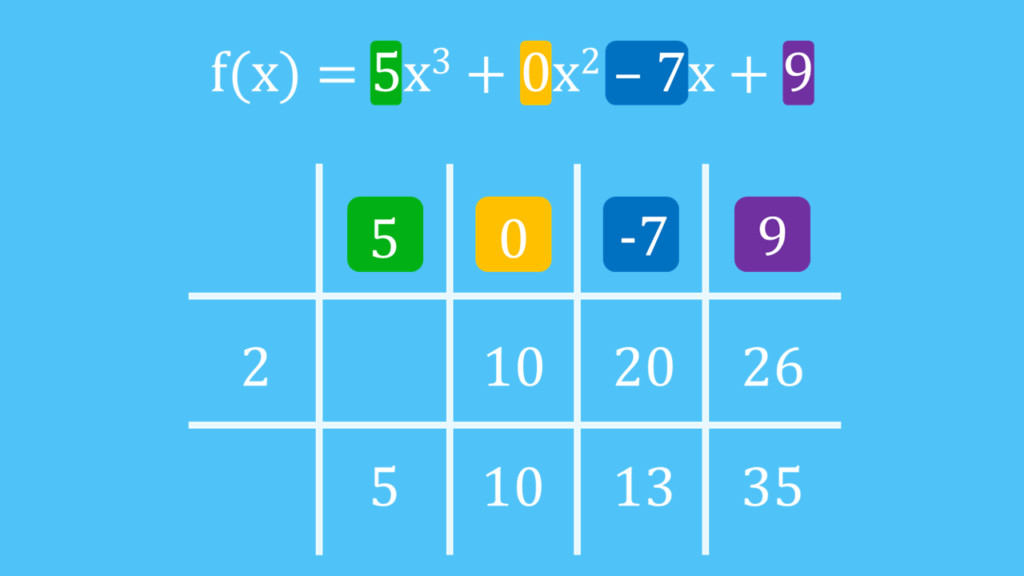
Diese Null musst du in die erste Zeile vom Horner Schema aufnehmen. Das Horner Schema für dieses Beispiel sieht dann folgendermaßen aus
Die Zahl in der dritten Zeile der letzten Spalte ist nicht Null. Das gibt dir den Hinweis, dass du es hier mit einer Polynomdivision mit Rest zu tun hast. Wie im vorherigen Beispiel, musst du die Koeffizienten in der letzten Zeile mit den „korrekten“ Termen kombinieren. Das bedeutet, dass du
die 5 mit 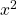 (und nicht
(und nicht 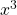 ),
),
die 10 mit 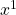 (und nicht
(und nicht 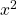 )
)
und die 13 mit 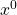 (und nicht
(und nicht 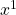 ) kombinierst.
) kombinierst.
Das Ergebnis dieser Polynomdivision lautet daher
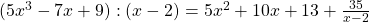 .
.
Polynomdivision
Eine weitere Möglichkeit Polynome durcheinander zu teilen ist die Polynomdivision . Damit du versteht, wie sie funktioniert, solltest du dir auf jeden Fall gleich noch unser Video daz anschauen! Bis gleich!