Normalenvektor
Du musst den Normalenvektor einer Ebene bestimmen? Im Video erfährst du, wie das geht!
Inhaltsübersicht
Normalenvektor einfach erklärt
Ein Normalenvektor (oder Normalvektor) ist ein Vektor, der senkrecht auf etwas anderem steht. Das kann eine Gerade, eine Ebene, eine Fläche oder auch eine gekrümmte Linie, wie zum Beispiel ein Kreis, sein. In der Mathematik sagt man statt senkrecht auch häufig, dass der Vektor orthogonal
zu etwas ist. Ein solcher Vektor wird in der Regel mit 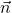 bezeichnet.
bezeichnet.
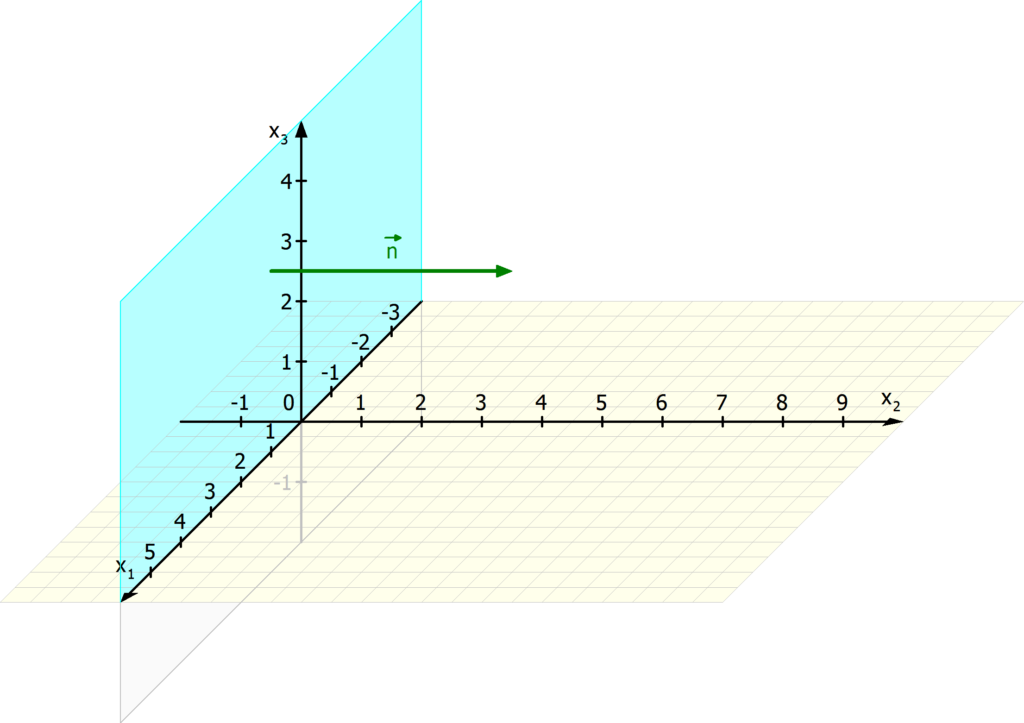
Meistens wirst du den Normalvektor 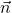 einer Ebene suchen. Das ist also ein Vektor, der senkrecht auf der Ebene steht, so wie im Bild.
einer Ebene suchen. Das ist also ein Vektor, der senkrecht auf der Ebene steht, so wie im Bild.
Normalenvektor Ebene
Für jede Darstellung einer Ebene kannst du einen Normalenvektor bestimmen.
Normalenform einer Ebene
Hier ist es besonders leicht, den Normalvektor zu bestimmen. Du kannst ihn nämlich einfach ablesen.
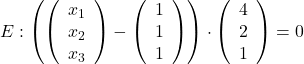
In diesem Beispiel ist der Normalvektor 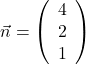 .
.
In der allgemeinen Normalenform
siehst du auch nochmal den Normalenvektor 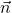 .
.
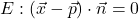
Koordinatenform einer Ebene
Auch hier kannst du den Normalvektor einfach wieder ablesen. Schau dir zunächst das Beispiel an.
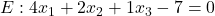
Hier setzt sich der gesuchte Vektor aus den Zahlen vor 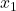 ,
, 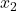 und
und 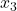 zusammen.
zusammen.
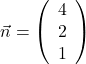
Das erkennst du auch in der allgemeinen Koordinatenform .
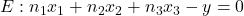 mit
mit 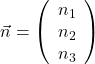
Parameterform einer Ebene
In diesem Fall kannst du den Normalvektor leider nicht so einfach ablesen. Stattdessen musst du ihn berechnen.
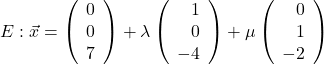
Dafür bildest du das Kreuzprodukt
aus den sogenannten Richtungsvektoren
, also dem Vektor hinter 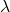 und dem Vektor hinter
und dem Vektor hinter 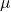 .
.
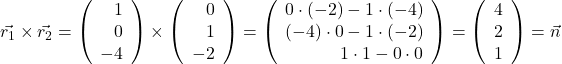
Das funktioniert bei jeder Ebene in Parameterform . Die allgemeine Ebene
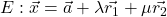
hat somit den Normalenvektor 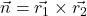 .
.
Normalenvektor Gerade
Du kannst aber auch einen Normalenvektor zu einer Gerade bestimmen. Hier siehst du ein Beispiel für eine Geradengleichung.
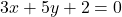
Den Normalvektor der Gerade kannst du einfach wieder ablesen.
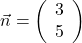
Allgemein hat eine Gerade also die Form
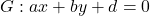 mit
mit 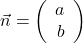 .
.
Beispiel
Diese Ebene ist wieder in Parameterform gegeben.
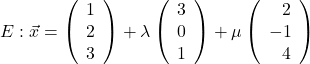
Jetzt kannst du wieder den Normalenvektor berechnen, indem du das Kreuzprodukt aus den Richtungsvektoren bildest.
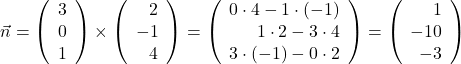
Normalenvektor – kurz & knapp
Der Normalenvektor (oder Normalvektor) ist in der Geometrie ein Vektor, der senkrecht (orthogonla) auf einem Objekt steht, zum Beispiel auf einer Ebene, Gerade, Kurve oder Fläche. Der Normalenvektor ist außerdem der Richtungsvektor der sogenannten Normale
.
Bei Ebenen berechnest du den Normalenvektor mit dem Kreuzprodukt oder du kannst ihn schon an der Geradengleichung ablesen.
Normalenform
Jetzt kannst du den Normalvektor einer Ebene ausrechnen. Du kannst mit seiner Hilfe aber auch Parameterform einer Ebene in die Koordinatenform umwandeln. Wie das geht, erfährst du hier !