Schnittpunkt zweier Geraden
Du willst den Schnittpunkt zweier Geraden berechnen? Hier und in unserem Video zeigen wir dir, wie’s geht!
Inhaltsübersicht
Schnittpunkt zweier Geraden einfach erklärt
Den Punkt, in dem sich zwei Geraden treffen, nennst du Schnittpunkt. Du kannst ihn auf zwei Arten bestimmen.
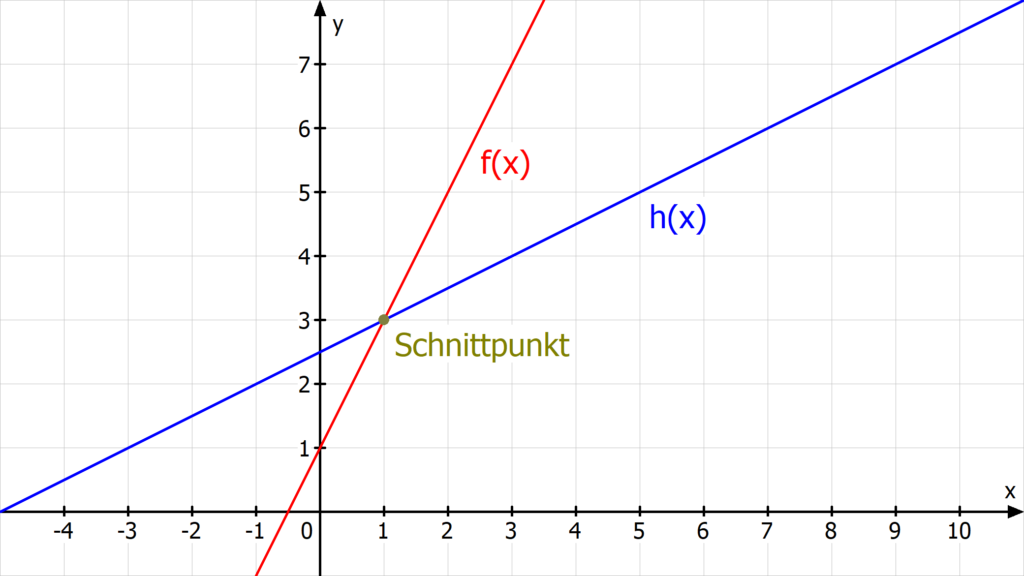
Liegt dein Schnittpunkt direkt auf einem Kästchen, kannst du ihn ganz einfach ablesen. Hier schneiden sich die Graphen im Schnittpunkt S(1|3).
Ist die Zeichnung aber zu ungenau, musst du den Schnittpunkt rechnerisch bestimmen. Wie das geht, zeigen wir dir anhand unserer 5-Schritt-Anleitung!
Schnittpunkt zweier Geraden berechnen: Allgemeine Vorgehensweise
Mit dieser Anleitung kannst du jeden Schnittpunkt ganz einfach berechnen!
- Funktionen gleichsetzen.
- Nach x auflösen.
- y-Koordinate berechnen
- Probe: x in die zweite Gleichung einsetzen
- Schnittpunkt angeben
Schau dir nun an ein paar Beispielen an, wie du den Schnittpunkt zweier Geraden berechnest.
Beispiel 1
Gesucht wird der Schnittpunkt zweier Geraden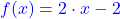 und
und 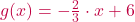 .
.
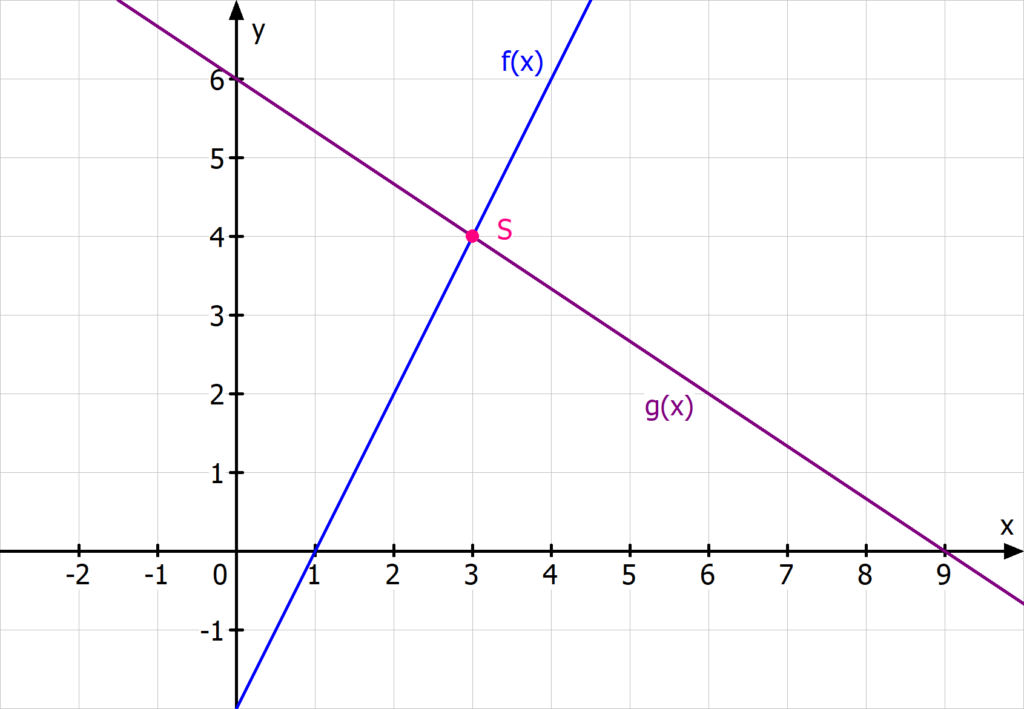
Graphisch kannst du die Koordinaten von S(3|4) zwar ablesen, du willst sie aber rechnerisch überprüfen:
Schritt 1: Funktionen gleichsetzen
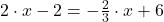
Schritt 2: Nach x auflösen
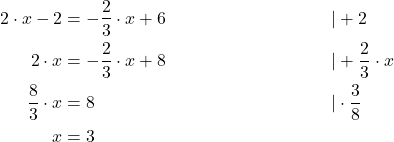
Schritt 3: y-Wert berechnen
Setze 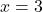 in
in 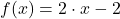 ein. Du erhältst als Ergebnis
ein. Du erhältst als Ergebnis 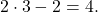
Schritt 4: Probe
Zur Probe setzt du 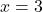 auch noch in
auch noch in 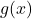 ein und erhältst
ein und erhältst
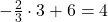
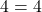
Schritt 5: Schnittpunkt angeben
Der Schnittpunkt der beiden Geraden ist S(3|4).
Beispiel 2
Gegeben sind die beiden Funktionsgraphen 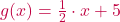 und
und 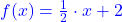 . Bestimme iheren Schnittpunkt!
. Bestimme iheren Schnittpunkt!
Auch hier kannst du wieder die 5 Schritte von oben anwenden, um den Schnittpunkt zweier Geraden zu berechnen.
Schritt 1: Funktionen gleichsetzen
![Rendered by QuickLaTeX.com \[ \frac{1}{2} \cdot x +5 = \frac{1}{2} \cdot x +2 \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b2224d56c3ddbc51bb8a06437e464162_l3.png)
Schritt 2: Nach x auflösen
![Rendered by QuickLaTeX.com \[ \frac{1}{2} \cdot x +5 = \frac{1}{2} \cdot x +2 \qquad | -\frac{1}{2} \cdot x \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e5bb360e75d146a3f8de65f054f6cd04_l3.png)

Das ist offensichtlich immer falsch! Dein falsches Ergebnis sagt dir, dass sich die Geraden nicht schneiden.
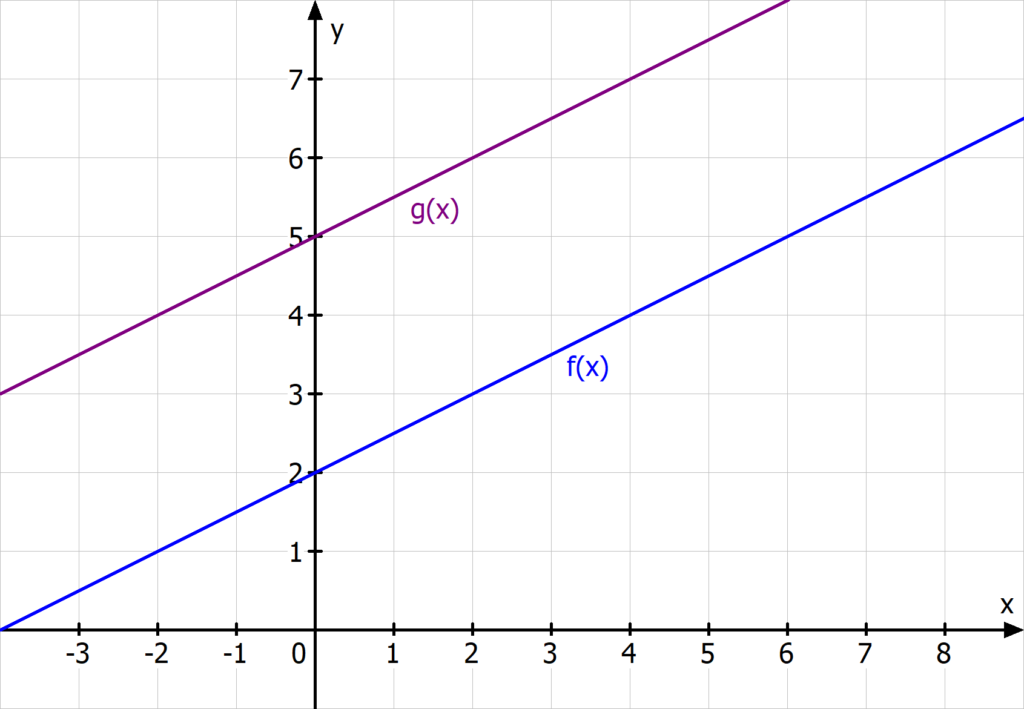
Das siehst du auch im Funktionsgraph: Hier haben die beiden Geraden dieselbe Steigung und damit keinen Schnittpunkt. Stattdessen sind sie echt parallel.
Einen Schnittpunkt gibt es nur, wenn die Steigung der Funktionsgleichungen nicht gleich ist.
- z. B. f(x) = 2x + 1 und h(x) = 0,5x + 2,5.
Haben zwei Funktionen dieselbe Steigung, sind sie entweder echt parallel (keinen Schnittpunkt) oder identisch (unendlich viele Schnittpunkte).
- z. B. f(x) = 1/2x + 2 und g(x) = 1/2x + 5
- oder f(x) = 3x – 4 und g(x) = 3x – 4
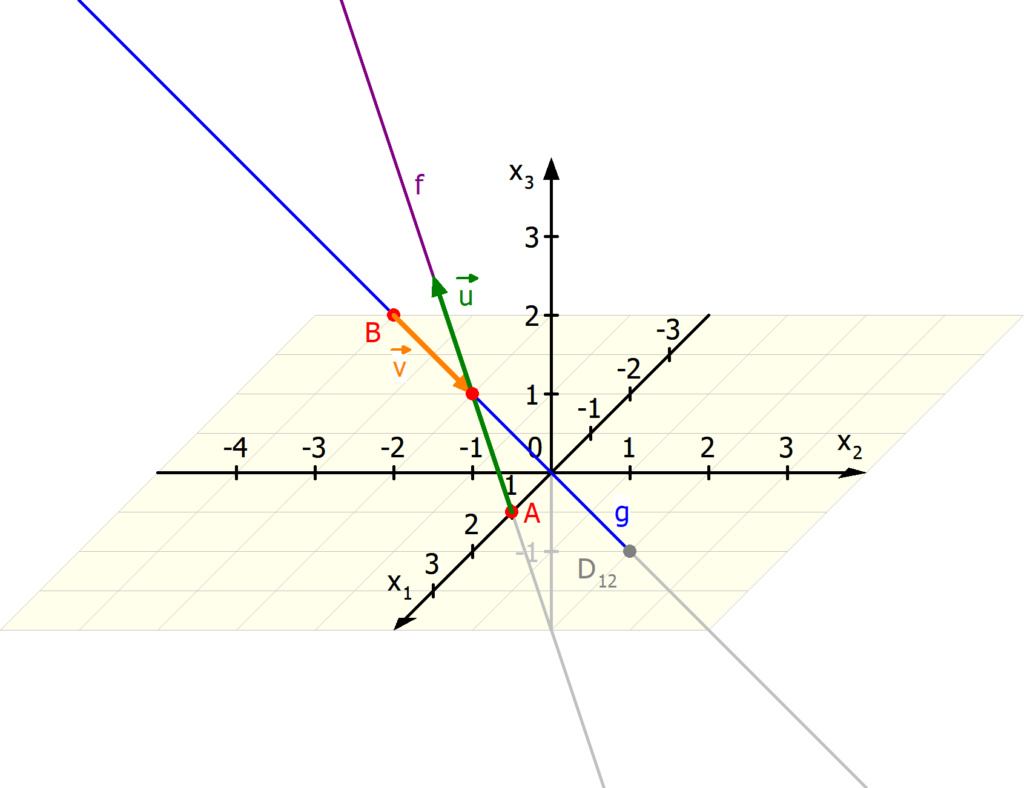
Schnittpunkt zweier Geraden: Vektordarstellung
In der analytischen Geometrie ist die Vektordarstellung von Geraden im Raum sehr verbreitet. Hier wird im Gegensatz zu oben die Gerade als Sammlung von Punkten interpretiert, wobei ausgehend von einem Aufpunkt die Richtung angegeben wird. Als Nächstes zeigen wir dir, wie du den Schnittpunkt zweier Geraden der folgenden Form berechnen kannst:
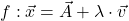 und
und 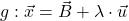
Die beiden Punkte 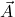 und
und 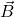 werden Aufpunkte der Geraden genannt,
werden Aufpunkte der Geraden genannt, 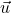 und
und 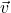 heißen Richtungsvektoren
.
heißen Richtungsvektoren
.
Schnittpunkt zweier Vektoren: Allgemeine Vorgehensweise
Da wir hier Geraden im dreidimensionalen Raum betrachten, ist die zeichnerische Methode um den Schnittpunkt zweier Geraden zu bestimmen, sehr unzuverlässig. Rechnerisch funktioniert es – so wie oben – durch Gleichsetzen der beiden linearen Funktionen. Wie genau du am besten vorgehst, beschreiben wir dir Schritt für Schritt:
-
Schritt 1: Um den Schnittpunkt zweier Geraden zu berechnen, betrachtest du zuerst die Richtungsvektoren
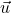 und
und 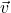 der beiden Geradengleichungen. Ist einer davon das Vielfache des anderen, das heißt sind die Vektoren linear abhängig
, dann sind die Geraden entweder identisch oder echt parallel. Um das zu überprüfen, setzt du den Aufpunkt
der beiden Geradengleichungen. Ist einer davon das Vielfache des anderen, das heißt sind die Vektoren linear abhängig
, dann sind die Geraden entweder identisch oder echt parallel. Um das zu überprüfen, setzt du den Aufpunkt 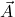 in die Gerade
in die Gerade 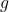 ein und prüfst, ob du
ein und prüfst, ob du 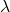 eindeutig bestimmen kannst.
eindeutig bestimmen kannst. - Schritt 2: Sind die beiden Richtungsvektoren linear unabhängig, so kannst du entweder den Schnittpunkt der Vektoren berechnen, oder die Geraden sind windschief. Um das herauszufinden, setzt du die beiden Funktionsgleichungen gleich und löst das zugehörige lineare Gleichungssystem.
- Schritt 3: Nun setzt du den errechneten x-Wert in eine der beiden Geradengleichungen ein, um die y-Koordinate des Schnittpunktes zu berechnen.
Diese Vorgehensweise um den Schnittpunkt zweier Geraden zu berechnen, zeigen wir dir am besten direkt an einigen Beispielen.
Achtung: Es kann sein, dass du den Schnittpunkt zweier Geraden im Raum nicht berechnen kannst, obwohl sie linear unabhängige Richtungsvektoren haben! Im Raum können sich auch Geraden nicht schneiden, obwohl sie nicht parallel sind! Sie liegen sozusagen in unterschiedlichen Ebenen. Solche Geraden nennt man windschief!
Beispiel 1
Gegeben sind die beiden Funktionen
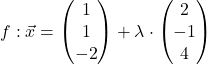 und
und 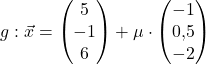 .
.
Zuerst überprüfen wir, ob die beiden Richtungsvektoren 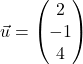 und
und 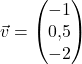 linear abhängig oder linear unabhängig sind. Damit siehst du sofort, ob es einen Schnittpunkt zweier Geraden überhaupt gibt.
linear abhängig oder linear unabhängig sind. Damit siehst du sofort, ob es einen Schnittpunkt zweier Geraden überhaupt gibt.
Durch scharfes Hinsehen oder Lösen des zugehörigen linearen Gleichungssystems sehen wir, dass die beiden Vektoren 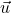 und
und 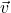 mit
mit 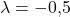 linear abhängig sind. Die Geraden
linear abhängig sind. Die Geraden 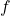 und
und 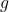 sind somit entweder identisch oder echt parallel. Um das herauszufinden, setzen wir den Punkt
sind somit entweder identisch oder echt parallel. Um das herauszufinden, setzen wir den Punkt 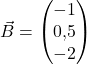 in
in 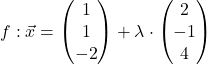 ein und berechnen
ein und berechnen 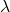
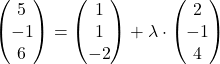
(I) 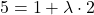
(II) 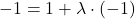
(III) 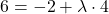
Für 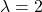 sind alle drei Gleichungen erfüllt. Das bedeutet, dass
sind alle drei Gleichungen erfüllt. Das bedeutet, dass 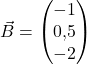 auf beiden Geraden liegt. Daher sind sie identisch und nicht echt parallel.
auf beiden Geraden liegt. Daher sind sie identisch und nicht echt parallel.
Beispiel 2
Den Schnittpunkt zweier Geraden in Vektordarstellung wollen wir in diesem Beispiel berechnen. Dafür sei gegeben:
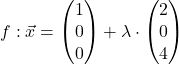 und
und 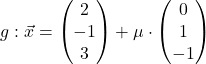
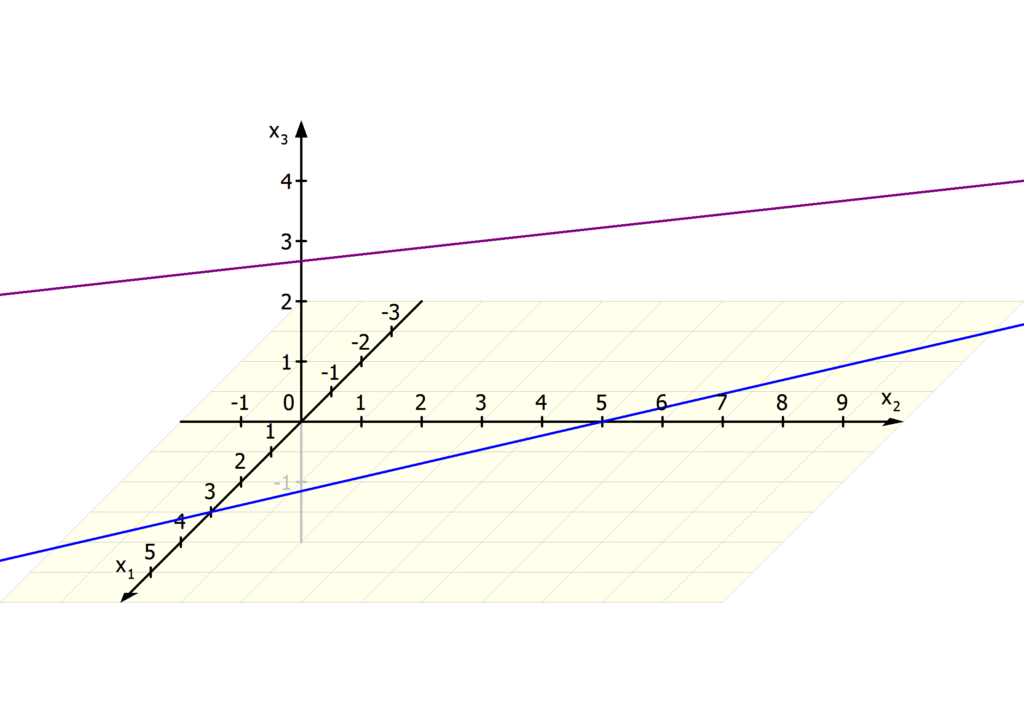
Hier sind die beiden Richtungsvektoren 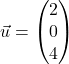 und
und 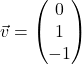 linear unabhängig. Um herauszufinden, ob wir den Schnittpunkt zweier Geraden berechnen können, oder ob sie windschief zueinander liegen, setzen wir die beiden Funktionen gleich:
linear unabhängig. Um herauszufinden, ob wir den Schnittpunkt zweier Geraden berechnen können, oder ob sie windschief zueinander liegen, setzen wir die beiden Funktionen gleich:
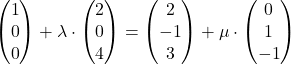
(I) 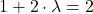
(II) 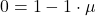
(III) 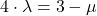
Aus (I) folgt direkt, dass hier 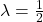 gelten muss und aus (II) bestimmen wir
gelten muss und aus (II) bestimmen wir 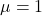 . Nun setzen wir beides in die dritte Gleichung ein und erhalten
. Nun setzen wir beides in die dritte Gleichung ein und erhalten 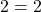 . Damit schneiden sich die beiden Geraden und wir können den Schnittpunkt zweier Geraden durch Einsetzen von
. Damit schneiden sich die beiden Geraden und wir können den Schnittpunkt zweier Geraden durch Einsetzen von 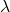 oder
oder 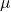 berechnen:
berechnen:
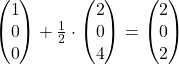
Übrigens: Noch mehr zum Schnittpunkt von Vektoren findest du in unserem Artikel Schnittpunkt berechnen .
y Achsenabschnitt berechnen
Super! Du kannst jetzt den Schnittpunkt zweier Geraden berechnen. In unserem Video zum Y Achsenabschnitt zeigen wir dir, wie du den Schnittpunkt mit der Y-Achse berechnen kannst. Schau es dir gleich an!