Substitution
Hier erklären wir dir, was eine Substitution ist und wie du mit dem Substitutionsverfahren Gleichungen lösen kannst. Schau dir am besten auch gleich unser Video dazu an!
Inhaltsübersicht
Was ist eine Substitution?
Stell dir vor, du willst die Lösung der folgenden Gleichung berechnen: 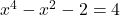 . Was auf den ersten Blick schwierig aussieht, kannst du mit einer Substitution und Resubstitution leicht lösen. Hierfür ersetzt du
. Was auf den ersten Blick schwierig aussieht, kannst du mit einer Substitution und Resubstitution leicht lösen. Hierfür ersetzt du 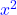 durch die neue Variable
durch die neue Variable  und löst du die Gleichung in vier Schritten:
und löst du die Gleichung in vier Schritten:
1. Substitution: Du ersetzt in der Gleichung 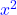 durch
durch  .
.
2. Berechnung von  : Das machst du zum Beispiel mit Hilfe der Mitternachts- oder pq-Formel
: Das machst du zum Beispiel mit Hilfe der Mitternachts- oder pq-Formel
3. Resubstitution: Nun ersetzt du  wieder durch
wieder durch 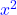 .
.
4. Berechnung von  : Nachdem du
: Nachdem du  kennst, kannst du jetzt auch
kennst, kannst du jetzt auch  leicht berechnen.
leicht berechnen.
Im folgenden Beispiel zeigen wir dir, wie du durch Substituieren die Lösungen einer Gleichung findest.
Substitution in Mathe – Beispiel
Lass uns als Beispiel die folgende Gleichung mit dem Substitutionsverfahren lösen:
![Rendered by QuickLaTeX.com \[x^4-x^2-2=4\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-dbd631cb2a4c6e9c82890f7b91f34d54_l3.png)
Als erstes bringst du alles auf eine Seite, indem du 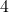 auf beiden Seiten abziehst.
auf beiden Seiten abziehst.
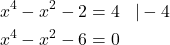
Dann stellst du fest, dass du diese Gleichung auch umschreiben kannst.
![Rendered by QuickLaTeX.com \[({\textcolor{blue}{x^2})^2-\textcolor{blue}{x^2}-6&=0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e65b21868eaa05b4155655c9dbdbc17e_l3.png)
Wenn in einer Gleichung als Variablen nur 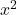 und
und 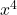 vorkommen, kannst du sie immer durch Substituieren lösen. Das ist zum Beispiel hier der Fall:
vorkommen, kannst du sie immer durch Substituieren lösen. Das ist zum Beispiel hier der Fall:
![Rendered by QuickLaTeX.com \[x^4-x^2-6=0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e8037fca5fd2666698f09b0b1711c283_l3.png)
Schauen wir uns jetzt an, wie du Schritt für Schritt vorgehst:
1. Substitution: Du ersetzt 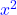 durch
durch  , sodass du eine vereinfachte Gleichung erhältst.
, sodass du eine vereinfachte Gleichung erhältst.
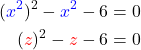
2. Berechnung von  : Jetzt kannst du diese Gleichung mit der Mitternachtsformel
(alternativ p-q-Formel
) lösen:
: Jetzt kannst du diese Gleichung mit der Mitternachtsformel
(alternativ p-q-Formel
) lösen:
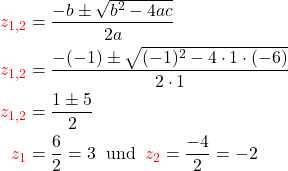
3. Resubstitution:  ersetzt du nun wieder durch
ersetzt du nun wieder durch 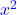 :
:

4. Berechnung von  : Nun musst du nach
: Nun musst du nach  auflösen. Hierfür musst Du die Wurzel aus
auflösen. Hierfür musst Du die Wurzel aus 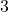 und
und 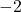 ziehen:
ziehen:
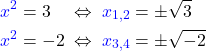
Vorsicht: Aus negativen Zahlen darfst du keine Wurzel ziehen! Das heißt also, dass es für 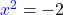 keine Lösung gibt.
keine Lösung gibt.
Deine zwei Lösungen lauten daher 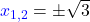 . Gar nicht so schwer, oder?
. Gar nicht so schwer, oder?
Weitere Übung im Substitutionsverfahren
Du willst das Substituieren noch einmal üben? Dann haben wir noch eine zweite Aufgabe für dich:
![Rendered by QuickLaTeX.com \[2x^4-18x^2+28=0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0f78e81f81c6ef7984c4454613c556ae_l3.png)
Diese Gleichung kannst du auch umschreiben:
![Rendered by QuickLaTeX.com \[2\cdot(\textcolor{blue}{x^2})^2-18\cdot\textcolor{blue}{x^2}+28=0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-24bde9e7066c54e5f2219a29d623a713_l3.png)
1. Substitution: Als Erstes musst du 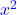 durch
durch  substituieren.
substituieren.
![Rendered by QuickLaTeX.com \[2\cdot(\textcolor{red}{z})^2-18 \cdot\textcolor{red}{z}+28=0\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0ef22b67e3c92b6fc9649ca4da2ffb4c_l3.png)
2. Berechnung von  : Jetzt kannst du
: Jetzt kannst du  mit der Mitternachtsformel leicht bestimmen.
mit der Mitternachtsformel leicht bestimmen.
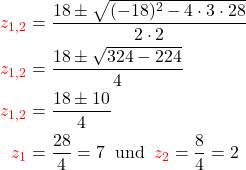
3. Rücksubstitution: Das Substitut  ersetzt du wieder durch
ersetzt du wieder durch 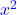 .
.

4. Berechnung von  : Nun löst du nach
: Nun löst du nach  auf.
auf.
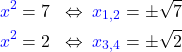
Durch Substituieren hast du die Lösungen für  herausgefunden. Sie lauten:
herausgefunden. Sie lauten:
![Rendered by QuickLaTeX.com \[\textcolor{blue}{x_1}=\sqrt{2}, \textcolor{blue}{x_2}=-\sqrt{2}, \textcolor{blue}{x_3}=\sqrt{7}, \textcolor{blue}{x_4}=-\sqrt{7} \]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-18b11a31fe9b2ced13aee5d41e408701_l3.png)
Unter Substitution versteht du das Ersetzen eines bestimmten Terms einer Gleichung durch eine einzelne Variable. Dadurch vereinfacht sich das Lösen der Gleichung. Du ersetzt also etwas Schwierigeres durch etwas Einfacheres und tauscht es nach der Berechnung wieder zurück.
Quadratische Ergänzung
Das Substitutionsverfahren ist nur eine Möglichkeit, in Mathe Gleichungen nach x aufzulösen. Damit du für deine nächste Prüfung auch wirklich gut vorbereitet bist, schau dir gleich noch unser Video zur quadratischen Ergänzung an – eine weitere gute Methode, um x zu bestimmen!