Brüche dividieren
Wie kannst du Brüche dividieren? Das erklären wir dir hier an vielen Beispielen. Am Ende findest du Aufgaben zum Üben. Schau dir unser Video an, um die Division von Brüchen anschaulich erklärt zu bekommen.
Wie dividiert man Brüche?
Beim Bruchrechnen kannst du Brüche dividieren (geteilt rechnen), indem du den ersten Bruch mit dem Kehrwert des zweiten Bruchs multiplizierst , also malnimmst.
Sollst du zum Beispiel
![\[\frac{1}{5}:\frac{\textcolor{blue}{3}}{\textcolor{red}{4}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-69adf68e037e5495018158a145ed4bf1_l3.png "Rendered by QuickLaTeX.com")
berechnen, dann bildest du zuerst den Kehrbruch, indem du Zähler und Nenner des zweiten Bruchs vertauschst.
![\[\frac{\textcolor{blue}{3}}{\textcolor{red}{4}} \to \frac{\textcolor{red}{4}}{\textcolor{blue}{3}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b6535343d7c8b3317199bd9c65d3eb65_l3.png "Rendered by QuickLaTeX.com")
Danach wandelst du die Division „:“ in eine Multiplikation „⋅“ um. Ersetze „:“ durch „⋅“.
![\[\frac{1}{5}\,: \,\frac{\textcolor{blue}{3}}{\textcolor{red}{4}}=\frac{1}{5}\,\cdot\,\frac{\textcolor{red}{4}}{\textcolor{blue}{3}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d9bbed2810e0e4a1616dc60af450846d_l3.png "Rendered by QuickLaTeX.com")
Anschließend berechnest du
das Ergebnis.
![\[\frac{1}{5}\,: \,\frac{\textcolor{blue}{3}}{\textcolor{red}{4}}=\frac{1}{5}\,\cdot\,\frac{\textcolor{red}{4}}{\textcolor{blue}{3}}=\frac{4}{15}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-887ae74710ef00d1db8082196c320871_l3.png "Rendered by QuickLaTeX.com")
Erinnerung: Brüche multiplizierst du, indem du Zähler mal Zähler und Nenner mal Nenner rechnest.
1. Lass den ersten Bruch stehen.
2. Ersetze das Geteiltzeichen durch ein Malzeichen.
3. Tausche im zweiten Bruch Zähler und Nenner (Kehrbruch).
4. Multipliziere die beiden Zähler.
5. Multipliziere die beiden Nenner.
6. Kürze das Ergebnis, wenn möglich.
Bruch durch Bruch teilen
Wie rechnet man Brüche geteilt? Schau dir dazu gleich ein Beispiel an.
![\[\frac{1}{6}\,:\,\frac{3}{7}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-abaac1727a983c169cca5a0bf8f88c56_l3.png "Rendered by QuickLaTeX.com")
1. Lass den ersten Bruch stehen:
![\[\frac{1}{6}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e4edf10c6f0129d09a0df65b38b80d19_l3.png "Rendered by QuickLaTeX.com")
2. Ersetze das Geteiltzeichen durch ein Malzeichen:
![\[\frac{1}{6} \cdot\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-5df64d84035630c96af8daf31ff7f441_l3.png "Rendered by QuickLaTeX.com")
3. Bilde den Kehrbruch: Berechne den Kehrwert des zweiten Bruchs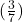 
, durch den geteilt werden soll. Dafür tauschst du den Zähler 3 mit dem Nenner 7.
![\[\frac{\textcolor{blue}{3}}{\textcolor{red}{7}} \to \frac{\textcolor{red}{7}}{\textcolor{blue}{3}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c6fda84613d9178adaaccf664ac20a1f_l3.png "Rendered by QuickLaTeX.com")
![\[\implies \frac{1}{6} \cdot \frac{\textcolor{red}{7}}{\textcolor{blue}{3}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b1d30af5c953e8b8bc4e6c3df4a7a4e1_l3.png "Rendered by QuickLaTeX.com")
4. und 5. Multipliziere die beiden Brüche: Beim Multiplizieren rechnest du Zähler mal Zähler und Nenner mal Nenner.
![\[\frac{1}{6}\,:\,\frac{\textcolor{blue}{3}}{\textcolor{red}{7}}=\frac{1}{6}\,\cdot\,\frac{\textcolor{red}{7}}{\textcolor{blue}{3}}=\frac{1\,\cdot\,7}{6\,\cdot\,3}=\frac{7}{18}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-db8a6f340e85ecb3f8e6013e7a2f4900_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{9}{10}\,:\,\frac{\textcolor{blue}{2}}{\textcolor{red}{7}} = \frac{9}{10}\,\cdot\,\frac{\textcolor{red}{7}}{\textcolor{blue}{2}}=\frac{9\,\cdot\,\textcolor{red}{7}}{10\,\cdot\,\textcolor{blue}{2}}=\frac{63}{20}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8902d68b7ac9e4e135d08a4ccb1fc97a_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{5}{13}\,:(-\frac{\textcolor{blue}{2}}{\textcolor{red}{9}})= \frac{5}{13}\,\cdot\,\frac{(-\textcolor{red}{9})}{\textcolor{blue}{2}}=\frac{5\,\cdot\,(-\textcolor{red}{9})}{13\,\cdot\,\textcolor{blue}{2}}=\frac{(-45)}{26}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3efd9e48c9e8a554d1f09f8e306db3e6_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{11}{3}:\frac{\textcolor{blue}{7}}{\textcolor{red}{4}}=\frac{11}{3}\,\cdot\,\frac{\textcolor{red}{4}}{\textcolor{blue}{7}}=\frac{11\,\cdot\,\textcolor{red}{4}}{3\,\cdot\,\textcolor{blue}{7}}=\frac{44}{21}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-548d09215b38846842d361d2109d29e4_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{a}{b}:\frac{\textcolor{blue}{c}}{\textcolor{red}{d}} = \frac{a}{b}\,\cdot\,\frac{\textcolor{red}{d}}{\textcolor{blue}{c}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-08f354a97c303ae6474de38bcad9fdd4_l3.png "Rendered by QuickLaTeX.com")
Brüche dividieren mit ganzen Zahlen
Beim Dividieren von Brüchen durch ganze Zahlen, musst du die Zahl zuerst in einen Bruch umwandeln. Dazu schreibst du die Zahl als Zähler auf den Bruchstrich. Der Nenner ist bei ganzen Zahlen immer die 1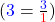 
.
- Ganze Zahl in einen Bruch umwandeln.
- Kehrwert des zweiten Bruchs berechnen.
- Division in Multiplikation umwandeln.
- Ergebnis berechnen.
Beispiel
![\[\frac{7}{3} : 5\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-287413871200e469951a726bf4c5aeb6_l3.png "Rendered by QuickLaTeX.com")
1. Zahl in einen Bruch umwandeln: Du kannst alle Zahlen auch als Bruch schreiben. Die Zahl ist dabei der Zähler. Der Nenner ist bei ganzen Zahlen immer 1.
![\[\frac{7}{3}:\textcolor{blue}{5} = \frac{7}{3}:\frac{\textcolor{blue}{5}}{1}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-4ac96995ef7aed1cb7e8f48078308f1d_l3.png "Rendered by QuickLaTeX.com")
Jetzt hast du wieder zwei Brüche und kannst wie im vorherigen Beispiel weitermachen.
2. Kehrwert berechnen: Vertausche Zähler und Nenner des zweiten Bruchs.
![\[\frac{\textcolor{blue}{5}}{\textcolor{red}{1}} \to \frac{\textcolor{red}{1}}{\textcolor{blue}{5}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-a88d4a155da9240972e59a9e24f7ca33_l3.png "Rendered by QuickLaTeX.com")
3. Division in Multiplikation umwandeln: Ersetze den zweiten Bruch durch den Kehrwert und aus „:“ (geteilt) wird „⋅“ (mal).
![\[\frac{7}{3}:\frac{\textcolor{blue}{5}}{\textcolor{red}{1}}=\frac{7}{3}\,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{5}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b1e384d20f286096f9c9bd34d2b9fe12_l3.png "Rendered by QuickLaTeX.com")
4. Ergebnis berechnen: Der Zähler 7 bleibt stehen, da er mit 1 multipliziert wird.
![\[\frac{7}{3} : 5=\frac{7\,\cdot\,\textcolor{red}{1}}{3\,\cdot\,\textcolor{blue}{5}} =\frac{7}{15}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-236eba42ab71279c48ed4edd0105cf22_l3.png "Rendered by QuickLaTeX.com")
Weitere Beispiele zum Dividieren von Brüchen
Hier findest du noch mehr Beispiele zum Dividieren von Brüchen:
![\[\frac{11}{5}:\textcolor{blue}{4}=\frac{11}{5}:\frac{\textcolor{blue}{4}}{\textcolor{red}{1}}=\frac{11}{5}\,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{4}}=\frac{11\,\cdot\,\textcolor{red}{1}}{5\,\cdot\,\textcolor{blue}{4}}=\frac{11}{20}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-07d2ddb87411637fdd2a1220e88385e4_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{3}{10}:\textcolor{blue}{2}=\frac{3}{10}:\frac{\textcolor{blue}{2}}{\textcolor{red}{1}}=\frac{3}{10}\,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{2}}=\frac{3\,\cdot\,\textcolor{red}{1}}{10\,\cdot\,\textcolor{blue}{2}}=\frac{3}{20}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8c4896de333d5cae7be15937ba3946ab_l3.png "Rendered by QuickLaTeX.com")
![\[\frac{3}{2}:\textcolor{blue}{7}=\frac{3}{2}:\frac{\textcolor{blue}{7}}{\textcolor{red}{1}}=\frac{3}{2}\,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{7}}=\frac{3}{14}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-0d0113e4142dc59aa18aa91752d61073_l3.png "Rendered by QuickLaTeX.com")
Bei der Division von Brüchen mit ganzen Zahlen muss die Zahl in einen Bruch umgewandelt werden. Dann hast du wieder 2 Brüche, die du, wie oben erklärt, teilen kannst.
![\[\frac{a}{b} : \textcolor{blue}{c} = \frac{a}{b} : \frac{\textcolor{blue}{c}}{\textcolor{red}{1}} = \frac{a}{b} \,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{c}}=\frac{a\,\cdot\,\textcolor{red}{1}}{b\,\cdot\, \textcolor{blue}{c}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-9b3a030e9b79ddb43e67d283267b0564_l3.png "Rendered by QuickLaTeX.com")
Gemischte Brüche dividieren
Es kann auch eine Division gegeben sein, die nicht nur Brüche beinhaltet. Manchmal
sollst du eine Mischung aus Zahl und Bruch dividieren (Gemischter Bruch). Dann musst du die gemischte Zahl vor dem Teilen in einen Bruch umwandeln.
- Gemischten Bruch
umwandeln. - Kehrwert berechnen.
- Division in Multiplikation umwandeln.
- Ergebnis berechnen.
Beispiel
![\[2\frac{2}{3}:\frac{7}{4}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1603b7dcc5a6f868c133a2361932cf60_l3.png "Rendered by QuickLaTeX.com")
1. Gemischten Bruch 
umwandeln: Dazu multiplizierst du die Zahl vor dem Bruch mit dem Nenner und addierst sie zum Zähler. Das wird dein neuer Zähler. Der Nenner bleibt dabei immer gleich.
![\[\textcolor{blue}{2}\frac{\textcolor{orange}{2}}{\textcolor{red}{3}}:\frac{7}{4}=\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{3}\,+\,\textcolor{orange}{2}}{\textcolor{red}{3}}:\frac{7}{4}=\frac{8}{3}:\frac{7}{4}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-88d1f09e4fba11a8aadfe216746c52b7_l3.png "Rendered by QuickLaTeX.com")
2. Kehrwert berechnen: Vertausche Zähler und Nenner des zweiten Bruchs.
![\[\frac{\textcolor{blue}{7}}{\textcolor{red}{4}} \to \frac{\textcolor{red}{4}}{\textcolor{blue}{7}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-e38005b50c106abb31ad40e21e5db2ad_l3.png "Rendered by QuickLaTeX.com")
3. Division in Multiplikation umwandeln: Ersetze den zweiten Bruch durch den Kehrwert und aus „:“ (geteilt) wird „⋅“ (mal).
![\[\frac{8}{3}:\frac{\textcolor{blue}{7}}{\textcolor{red}{4}}=\frac{8}{3}\,\cdot\,\frac{\textcolor{red}{4}}{\textcolor{blue}{7}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d20d0e7b017a6d2bd80c6e6460f2b3dc_l3.png "Rendered by QuickLaTeX.com")
4. Ergebnis berechnen
![\[\frac{8}{3}:\frac{\textcolor{blue}{7}}{\textcolor{red}{4}}=\frac{8}{3}\,\cdot\,\frac{\textcolor{red}{4}}{\textcolor{blue}{7}}= \frac{8\,\cdot\,\textcolor{red}{4}}{3\,\cdot\,\textcolor{blue}{7}}=\frac{32}{21}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6ef8c2905c7e0ac90af364f5392d588f_l3.png "Rendered by QuickLaTeX.com")
Weitere Beispiele: Brüche geteilt rechnen
Schau dir gleich noch ein paar Beispiele dazu an:
![\[\textcolor{blue}{3}\frac{1}{\textcolor{red}{3}}:\textcolor{blue}{2}\frac{1}{\textcolor{red}{8}}=\frac{\textcolor{blue}{3}\,\cdot\,\textcolor{red}{3}\,+\,1}{\textcolor{red}{3}}:\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{8}\,+\,1}{\textcolor{red}{8}}=\frac{10}{3}:\frac{\textcolor{blue}{17}}{\textcolor{red}{8}}=\frac{10}{3}\,\cdot\,\frac{\textcolor{red}{8}}{\textcolor{blue}{17}}=\frac{80}{51}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d6a88934ba10a34e4e5df1d19bec2c49_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{2}\frac{1}{\textcolor{red}{3}}:4=\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{3}\,+\,1}{\textcolor{red}{3}}:4=\frac{7}{3}:4=\frac{7}{3}:\frac{\textcolor{blue}{4}}{\textcolor{red}{1}}=\frac{7}{3}\,\cdot\,\frac{\textcolor{red}{1}}{\textcolor{blue}{4}}=\frac{7\,\cdot\,1}{3\,\cdot\,4}=\frac{7}{12}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b8edfd17b04cd0831cc0a5ab0492ca02_l3.png "Rendered by QuickLaTeX.com")
![\[5:\textcolor{blue}{2}\frac{2}{\textcolor{red}{5}}=\frac{5}{1}:\frac{\textcolor{blue}{2}\,\cdot\,\textcolor{red}{5}\,+\,2}{\textcolor{red}{5}}=\frac{5}{1}:\frac{\textcolor{blue}{12}}{\textcolor{red}{5}}=\frac{5}{1}\,\cdot\,\frac{\textcolor{red}{5}}{\textcolor{blue}{12}}=\frac{25}{12}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-8b2711ee42a889d40553ecfc9c84a66a_l3.png "Rendered by QuickLaTeX.com")
Bei der Division von gemischten Brüchen musst du die Zahl vor dem Bruch mit auf den Bruchstrich ziehen, indem du sie mit dem Nenner multiplizierst und zum Zähler addierst. Die restlichen Schritte ändern sich nicht.
![\[\textcolor{blue}{a}\frac{b}{\textcolor{red}{c}} : \frac{d}{e} = \frac{\textcolor{blue}{a}\,\cdot\,\textcolor{red}{c} \,+\,b}{\textcolor{red}{c}}:\frac{\textcolor{blue}{d}}{\textcolor{red}{e}}=\frac{a \cdot c + b}{c} \cdot \frac{\textcolor{red}{e}}{\textcolor{blue}{d}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-aff6d1c7dda10bfa329aa7c7e3bcd631_l3.png "Rendered by QuickLaTeX.com")
Brüche dividieren Aufgaben
Hier haben wir noch ein paar Übungsaufgaben zum Dividieren von Brüchen für dich vorbereitet. Berechne:
![\[\frac{12}{5}:\frac{6}{7}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c89125d132bf3660d3f36d3cae10a6bd_l3.png "Rendered by QuickLaTeX.com")
![\[7:\frac{3}{2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2057737991e4e91153278ee0f75972a9_l3.png "Rendered by QuickLaTeX.com")
![\[(-\frac{5}{7})\,:\,(-\frac{8}{14})\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6139c8ce1674a8b4743312c376aa6346_l3.png "Rendered by QuickLaTeX.com")
Jetzt kannst du überprüfen, ob du zu allen Brüche dividieren Aufgaben die richtige Lösung gefunden hast.
Lösung
![\[\frac{12}{5}:\frac{\textcolor{blue}{6}}{\textcolor{red}{7}}=\frac{12}{5}\,\cdot\,\frac{\textcolor{red}{7}}{\textcolor{blue}{6}}=\frac{12\,\cdot\,7}{5\,\cdot\,6}=\frac{84}{30}=\frac{14}{5}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-b830a19fe93464706c32b11be0b3c5fa_l3.png "Rendered by QuickLaTeX.com")
![\[\textcolor{blue}{7}:\frac{3}{2}=\frac{7}{1}:\frac{\textcolor{blue}{3}}{\textcolor{red}{2}}=\frac{7}{1}\,\cdot\,\frac{\textcolor{red}{2}}{\textcolor{blue}{3}}=\frac{7\,\cdot\,\textcolor{red}{2}}{1\,\cdot\,\textcolor{blue}{3}}=\frac{14}{3}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-f6391ee63779c30664b67a657f5f48fc_l3.png "Rendered by QuickLaTeX.com")
![\[(-\frac{5}{7})\,:\,(-\frac{\textcolor{blue}{8}}{\textcolor{red}{14}})=(-\frac{5}{7})\,\cdot\,(-\frac{\textcolor{red}{14}}{\textcolor{blue}{8}})=\frac{(-5)\,\cdot\,(-\textcolor{red}{14})}{7\,\cdot\,\textcolor{blue}{8}}=\frac{70}{56}=\frac{5}{4}=1\frac{1}{4}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-3dbff0e955dab6beddfad5d78a9a55f6_l3.png "Rendered by QuickLaTeX.com")
Bruchrechnung Aufgaben
Jetzt weißt du, wie man Brüche multiplizieren und dividieren kann. Wenn du jetzt noch mehr zum Thema Brüche erfahren willst, schau dir gleich unsere anderen Videos zum Bruchrechnen an.
In einem anderen Video zeigen wir dir außerdem viele typische Aufgaben mit Lösungen zur Division von Brüchen.
