Lineare Funktionen einfach erklärt
Du möchtest wissen, was lineare Funktionen sind, und suchst nach Beispielaufgaben? Dann bist du hier und im Video genau richtig.
Inhaltsübersicht
Lineare Funktionen einfach erklärt
Hier siehst du Beispiele für lineare Funktionen :
- f(x) = 3x + 7
- y = -2x + 0
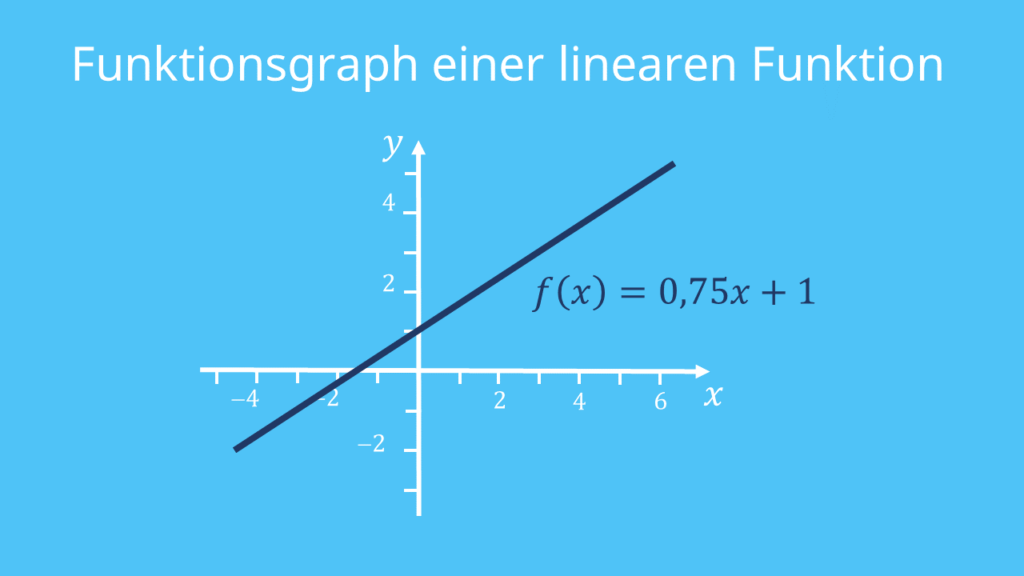
- f(x) = 0,75x + 1
Du kannst jede lineare Funktion auch als eine Gerade im Koordinatensystem zeichnen. Dabei gibt es verschiedene Arten von Geraden: Lineare Funktionen können steigen, fallen oder waagerecht im Koordinatensystem liegen. Die Gerade nennst du den Funktionsgraphen.
Merke: In einer linearen Funktion steht immer ein x, niemals eine andere Potenz, z.B. x2 oder x3. Deshalb kannst du sie auch Funktion ersten Grades nennen.
Lineare Funktionen Formel: y = m x + b
Jede lineare Funktion kannst du mathematisch als Gerade oder als Gleichung darstellen. Die Gleichung nennst du dann die Funktionsgleichung.
Jede Funktionsgleichung einer linearen Funktion hat die Form: 
Das m ist die sogenannte Steigung und das b der y-Achsenabschnitt deiner linearen Funktion. Zum Beispiel hat y = 3x + 7 die Steigung 3 und den y-Achsenabschnitt 7.
Was sie bedeuten und wie du sie berechnen kannst, erfährst du jetzt.
Steigung m
Das m in der Lineare-Funktionen-Formel sagt dir, wie stark deine Funktionsgerade steigt oder fällt. Dabei gibt es drei verschiedene Möglichkeiten:
- m > 0: Gerade steigt.
- m = 0: Gerade ist waagerechte.
- m < 0: Gerade fällt.
Am einfachsten kannst du die Steigung m so berechnen: direkt am Funktionsgraphen mithilfe eines Steigungsdreiecks .
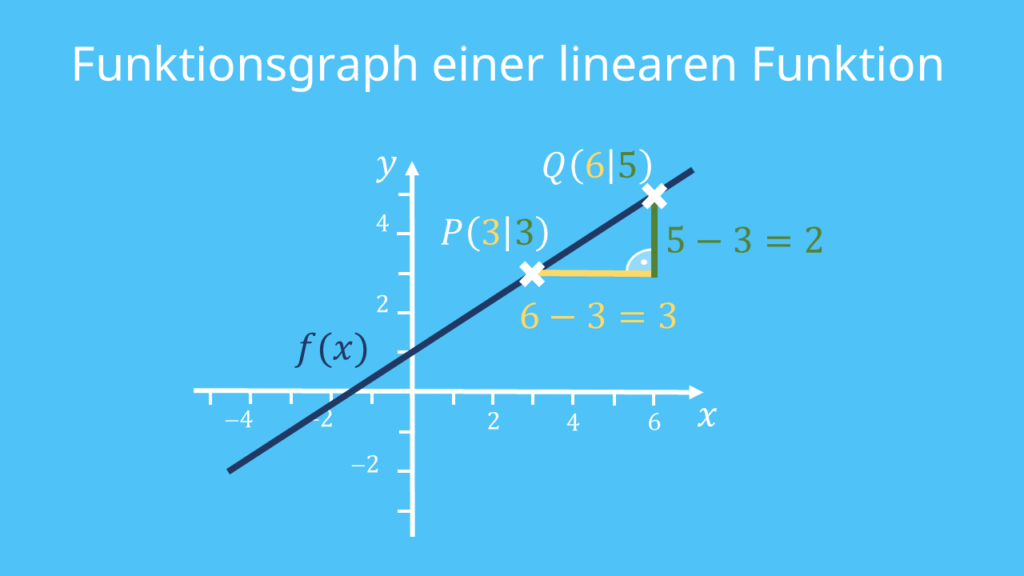
Dazu wählst du zuerst zwei beliebige Punkte auf der Gerade, zum Beispiel die Punkte P(3|3) und Q(6|5). (P liegt also 3 Einheiten in x-Richtung (rechts) und 3 Einheiten in y-Richtung (oben). Q findest du 6 Einheiten in x– und 5 in y-Richtung.)
Jetzt zeichnest du ein Steigungsdreieck ein, wie du es im Bild sehen kannst.
Für die Steigung m teilst du jetzt die Länge der senkrechten durch die Länge der waagerechten Seite deines Steigungsdreiecks. Hier ist die Steigung also 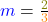 .
.
Du kannst die Steigung m aber auch berechnen. Dazu brauchst du nur diese Formel.
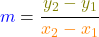
x1 ist der x-Wert des ersten Punktes P, also im Beispiel 3. x2 ist der x-Wert des zweiten Punktes Q, also 6. y1 und y2 sind die entsprechenden y-Werte.
Die Werte setzt du jetzt in die Formel für die Steigung ein.
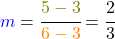 .
.
Deine Steigung beträgt also 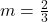 .
.
y-Achsenabschnitt b
Das b in der Funktionsgleichung f(x) = m x + b ist der y-Achsenabschnitt . Das ist der Wert, an dem die Gerade die y-Achse schneidet. Du siehst, dass die Gerade in unserem Beispiel die y-Achse an der Stelle 1 schneidet. Also ist der y-Achsenabschnitt b = 1.
Jetzt kennst du die Steigung m und den y-Achsenabschnitt b unserer Beispielfunktion. Also kannst du auch die Funktionsgleichung angeben. Dazu setzt du einfach m und b in die Standardgleichung f(x) = m x + b ein.
Unser Beispiel hat also die Funktionsgleichung 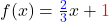 .
.
Jetzt weißt du, wie du Funktionsgleichungen bestimmst. Du berechnest m und b und setzt sie in y = m x + b ein.
Alle Möglichkeiten, wie du dabei vorgehen kannst, erklären wir dir ausführlich im Artikel Funktionsgleichung .
Nullstellen berechnen: Lineare Funktionen
Du kannst aber auch die Stelle berechnen, an der eine lineare Funktion die x-Achse schneidet. Das nennst du die Nullstelle.
Um die Nullstelle zu berechnen, setzt du eine 0 für das y in deiner Gleichung ein.
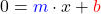
Die Gleichung löst du dann nach x auf. Für die Funktion y = -2 x + 1 erhältst du also zum Beispiel
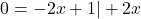
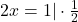
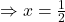
Also hat deine Funktion bei 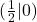 eine Nullstelle. Der y-Wert der Nullstelle ist nämlich immer 0.
eine Nullstelle. Der y-Wert der Nullstelle ist nämlich immer 0.
Du musst die Gleichung aber auch nicht jedes Mal lösen. Die Nullstelle ist immer:
![Rendered by QuickLaTeX.com \[x = - \cfrac{\textcolor{red}{b}}{\textcolor{blue}{m}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c3c05d24588ea26885e9fd53a287a7cb_l3.png)
Ausführlich erklärt findest du das im Artikel Nullstellen berechnen . Dort zeigen wir dir auch mehrere Beispiele, wie du die Nullstellen berechnen kannst.
Lineare Funktionen zeichnen
Schau dir das am Beispiel 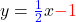 an.
an.
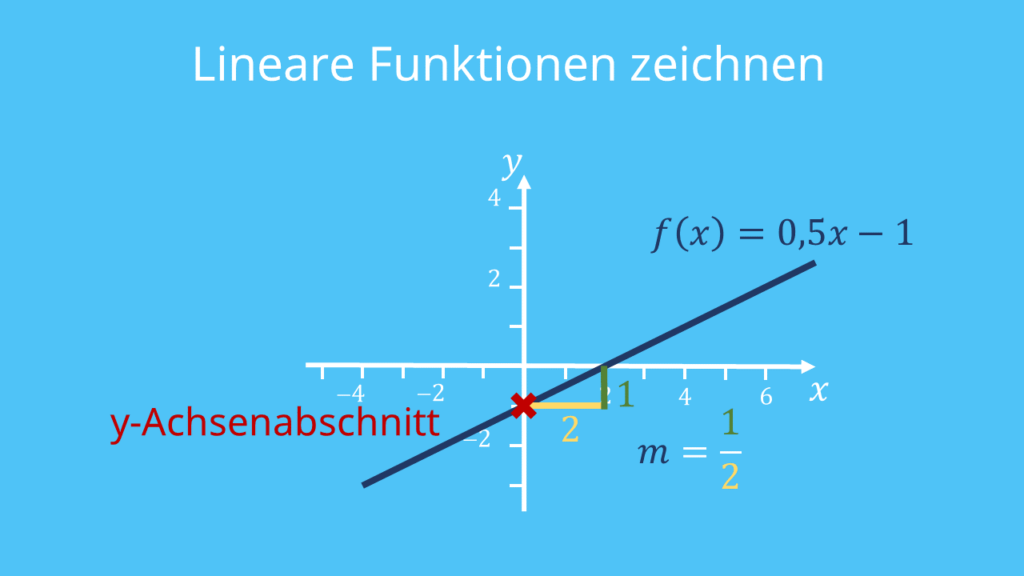
Zeichne als erstes den Schnittpunkt mit der y-Achse ein. Den kannst du einfach ablesen, denn das ist b = – 1.
Als nächstes zeichnest du mithilfe der Steigung das Steigungsdreieck. Bei 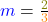 müsstest du 3 nach rechts und 2 nach oben. Bei
müsstest du 3 nach rechts und 2 nach oben. Bei 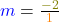 müsstest du 1 nach rechts und 2 nach unten gehen. Positive Steigung nach oben, negative nach unten.
müsstest du 1 nach rechts und 2 nach unten gehen. Positive Steigung nach oben, negative nach unten.
In unserem Beispiel ist 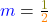 . Deshalb musst du von deinem Schnittpunkt mit der y-Achse aus 2 nach rechts und 1 nach oben.
. Deshalb musst du von deinem Schnittpunkt mit der y-Achse aus 2 nach rechts und 1 nach oben.
Jetzt zeichnest du nur noch die Gerade durch beide Punkte deines Steigungsdreiecks und bist fertig.
Besonderheiten waagerechter und senkrechter Geraden
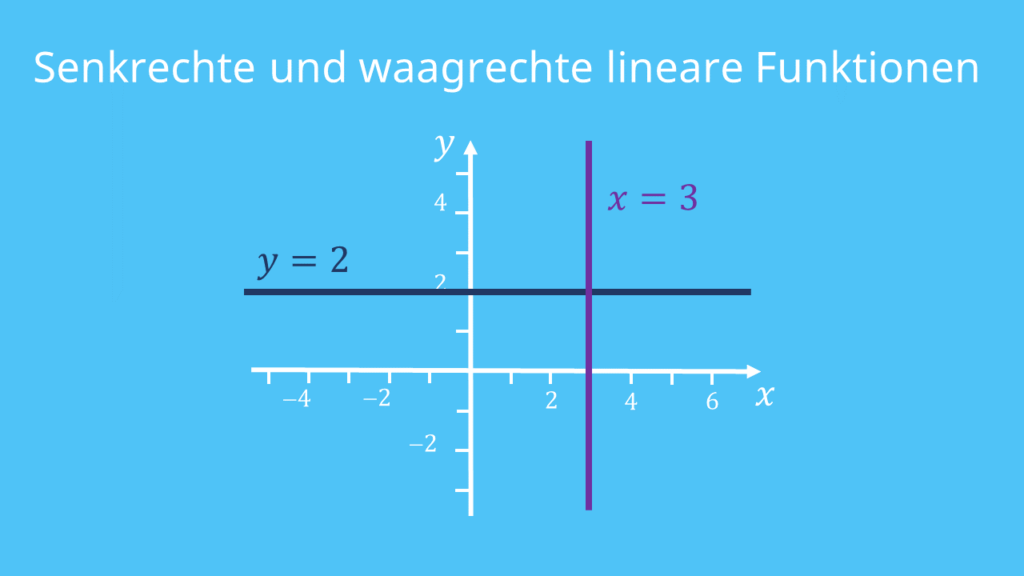
Eine Besonderheit stellen die waagerechten und die senkrechten Geraden im Koordinatensystem dar. Waagerechte lineare Funktionen haben immer die Steigung m = 0 und damit die Funktionsgleichung f(x) = b. Hier kannst du kein Steigungsdreieck einzeichnen. Außerdem hat sie keine Nullstelle. (Sonderfall f(x) = 0 hat unendlich viele Nullstellen).
Der andere Spezialfall sind die senkrechten Geraden. Aber Achtung: Das sind KEINE linearen Funktionen. Ihre Steigung ist unendlich. Und ihre Gleichung ist x = c. Dabei ist c eine beliebige Zahl. Du kannst die senkrechte Gerade also nicht als y = m x + b darstellen.
Hinweis: Noch mehr Details dazu erfährst du in unserem Experten-Video zu linearen Funktionen !
Lage von Geraden
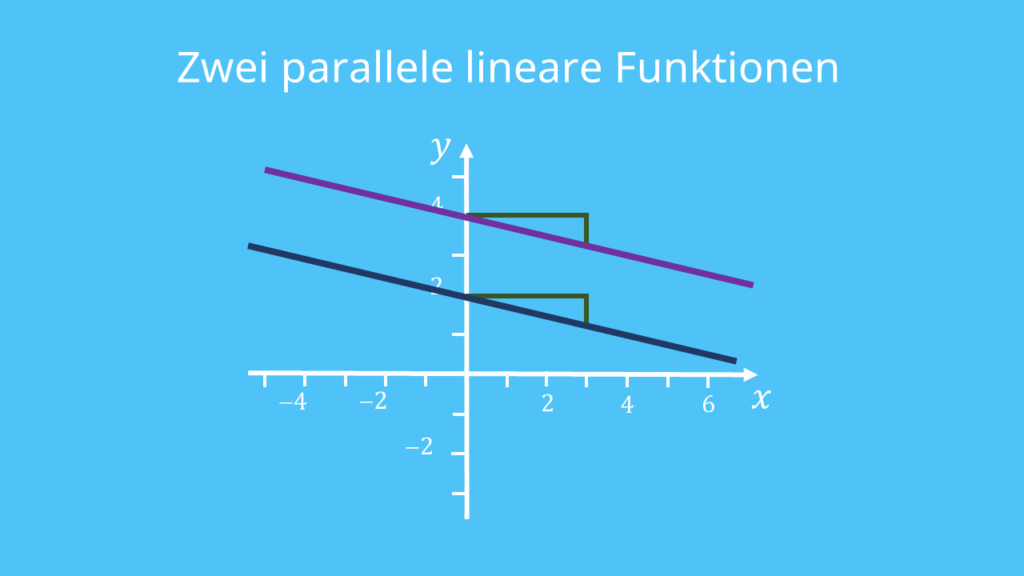
Es gibt zwei verschiedene Möglichkeiten, wie zwei lineare Funktionen in einem Koordinatensystem zueinander liegen können. Entweder sind zwei lineare Funktionen parallel oder sie haben einen eindeutigen Schnittpunkt.
Du erkennst zwei parallele Geraden immer daran, dass sie dieselbe Steigung haben.
Hast du zwei parallele lineare Funktionen gegeben, so musst du lediglich unterscheiden, ob sie echt parallel sind oder identisch.
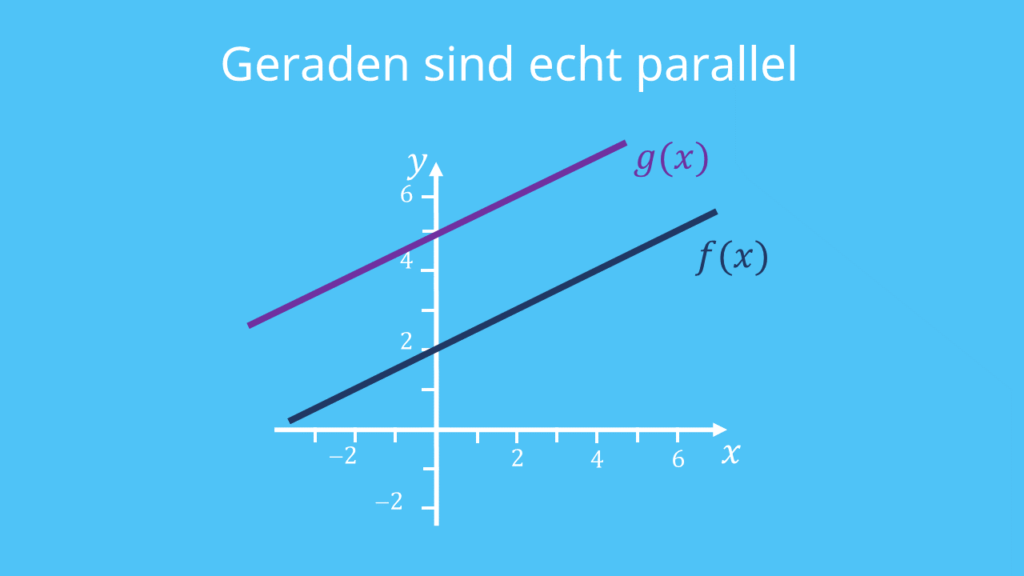
Echt parallel bedeutet, dass die Geraden keinen gemeinsamen Punkt haben, so wie im Bild. Identisch bedeutet, dass beide Geraden gleich sind. Sie haben also genau die gleiche Funktionsgerade.
Ob zwei Geraden mit gleicher Steigung echt parallel oder identisch sind, erkennst du sofort am y-Achsenabschnitt.
| Steigung m | y-Achsenabschnitt b | Lage der Geraden |
| unterschiedlich | unterschiedlich | eindeutiger Schnittpunkt |
| unterschiedlich | gleich | eindeutiger Schnittpunkt |
| gleich | unterschiedlich | echt parallel |
| gleich | gleich | identisch |
Lineare Funktionen Aufgaben
Im Folgenden findest du verschiedene Übungen mit Lösungen zum Thema Lineare Funktionen.
Lineare Funktionen Aufgaben 1 a) und b)
a) Zeichne die Gerade durch die beiden Punkte 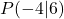 und
und 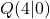 .
.
b) Bestimme die zugehörige Funktionsgleichung.
Lineare Funktionen Aufgaben 2 a) und b)
Überprüfe zwei lineare Funktionen auf ihre Lage im Koordinatensystem.
a) 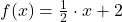 und
und 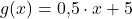
b) 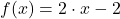 und
und 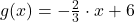
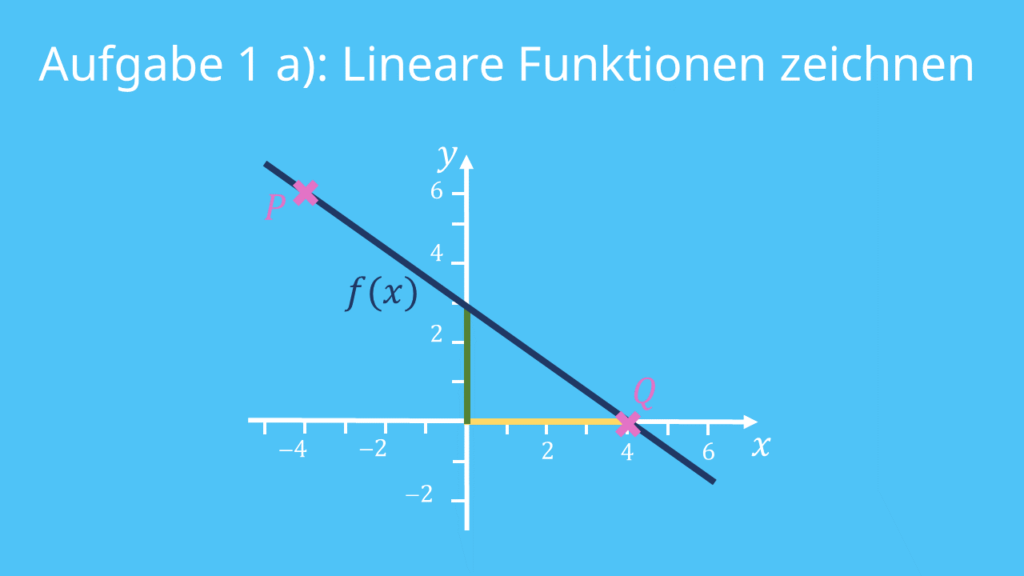
Lösung Aufgaben 1 a) und b)
a) Die Gerade sieht folgendermaßen aus:
b) Du kannst ablesen, dass b = 3 gelten muss. Um die Steigung zu berechnen, betrachtest du das Steigungsdreieck, das die Gerade mit den beiden Koordinatenachsen einschließt. Hier gehst du 4 Schritte nach links und 3 nach oben. Weil du nach links gehst, setzt du -4 in die Formel ein. Somit ist 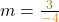 und
und
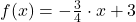 .
.
Lösung Aufgaben 2 a) und b)
a) Die Geraden haben dieselbe Steigung 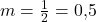 , aber einen unterschiedlichen y-Achsenabschnitt. Also sind sie echt parallel.
, aber einen unterschiedlichen y-Achsenabschnitt. Also sind sie echt parallel.
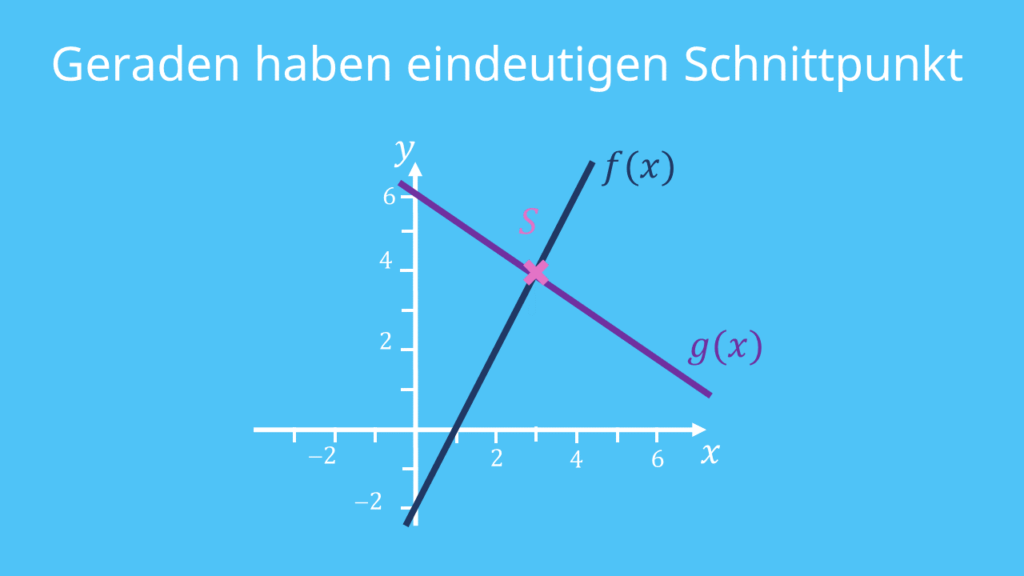
b) Die beiden Funktionen haben eine unterschiedliche Steigung, nämlich 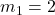 und
und 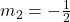 . Also haben sie einen eindeutigen Schnittpunkt.
. Also haben sie einen eindeutigen Schnittpunkt.
Lineare Funktionen — häufigste Fragen
-
Wie lautet die lineare Funktionen Formel?
Eine lineare Funktion ist immer eine Gerade. Ihre Gleichung ist y = m • x + b. Dabei ist m die Steigung und b der y-Achsenabschnitt.
-
Was ist eine lineare Funktion Übersicht?
Der Graph einer linearen Funktion ist eine Linie oder, mathematisch ausgedrückt, eine Gerade. Die lineare Funktionsgleichung lautet: f(x) = m • x + b.
-
Wie kann ich den y-Achsenabschnitt berechnen mit 2 Punkten?
Zuerst berechnest du die Steigung als Differenz aus den zwei Punkten. Um dann den y-Achsenabschnitt zu berechnen, setzt du einen der Punkte und die Steigung in die allgemeine Funktionsgleichung f(x) = m • x + b ein. Dann kannst du nach b auflösen.
Schnittpunkt zweier Geraden
Wie du einen solchen Schnittpunkt von zwei linearen Funktionen berechnest, erfährst du hier. Schau es dir gleich an!