Negative Potenzen
Was sind negative Potenzen und wie rechnest du sie aus? Hier und in unserem Video erfährst du alles, was du wissen musst!
Inhaltsübersicht
Negative Potenzen einfach erklärt
Eine Potenz ist eine Schreibweise, die du immer dann benutzt, wenn du eine Zahl öfter mit sich selbst mal nimmst. Die untere Zahl nennst du Basis (hier: 2) und die obere Zahl ist der Exponent (hier: 5).
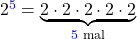
Bei negativen Potenzen hast du eine Basis mit negativem Exponenten. Zum Beispiel:
- 3 -4
- 5 -2
- 7 -6
Das liest du dann: drei hoch minus vier, fünf hoch minus zwei und sieben hoch minus sechs.
Damit du das Ergebnis ausrechnen kannst, formst du die negative Potenz um. Das machst du so: Du wandelst die negative Potenz in einen Bruch um. Oben schreibst du eine 1 und unten die Potenz ohne Minus-Zeichen.
Bei Potenzen mit negativem Exponenten entsteht bei der Umformung ein Bruch. Im Zähler steht eine 1 und im Nenner steht die Basis hoch der Exponent mal – 1. Also die Basis mit dem positiven Exponenten.
Negative Potenzen Beispiele
Schau dir die Umformungen von negativen Potenzen nochmal an ein paar Beispielen an:
Beispiel 1: 10-5
Um den negativen Exponenten aufzulösen, formst du die Potenz in einen Bruch um. Oben schreibst du eine 1 und unten die Basis hoch den positiven Exponenten.
![Rendered by QuickLaTeX.com \[10^{\textcolor{red}{-}\textcolor{blue}{5}} =\textcolor{red}{\frac{\textcolor{black}{1}}{\textcolor{black}{10}^\textcolor{blue}{5}}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2dc60cd1d694f1ad1f28562604684f99_l3.png)
Nun kannst du dein Ergebnis ganz einfach berechnen:
![Rendered by QuickLaTeX.com \[\frac{1}{10\cdot10\cdot10\cdot10\cdot10} = \frac{1}{100.000}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-c19f38ab57be076c2230be1280067ea1_l3.png)
Beispiel 2: 6-3
Oben in den Bruch schreibst du eine 1 und unten die Basis mit dem positiven Exponenten.
![Rendered by QuickLaTeX.com \[6^{\textcolor{red}{-}\textcolor{blue}{3}} =\textcolor{red}{\frac{\textcolor{black}{1}}{\textcolor{black}{6}^\textcolor{blue}{3}}}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-d8d07034599d378d2d8f017df4c11f29_l3.png)
Rechne nun dein Ergebnis aus:
![Rendered by QuickLaTeX.com \[\frac{1}{6\cdot6\cdot6} = \frac{1}{216}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-400d493d38908b0326012e9284e7d8b4_l3.png)
Super! Jetzt weißt du, wie man Potenzen mit negativen Exponenten auflöst! Schau dir jetzt an, wie dir die Potenzgesetze bei Potenzen mit negativen Hochzahlen helfen können.
Potenzgesetze negativer Exponent
Das 1. Potenzgesetz lautet:
Wenn zwei Potenzen dieselbe Basis haben und multipliziert ( · ) werden sollen, lässt du eine Basis stehen und addierst ( + ) die Exponenten.
Beispiel: 47 · 4-5 = 47+(-5) = 47-5 = 42
Das 2. Potenzgesetz lautet:
Wenn du zwei Potenzen mit gleicher Basis dividierst ( : ), lässt du eine Basis stehen und subtrahierst ( – ) die Exponenten.
Beispiel: 24 : 2-3 = 24–(-3) = 24+3 = 27
Das Ergebnis kann auch einen negativen Exponenten haben: Bei der Division von Potenzen mit gleicher Basis kommt es zu einem negativen Exponenten, wenn die Hochzahl des Zählers kleiner ist als die Hochzahl des Nenners. Beispiel: 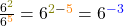
Das 3. Potenzgesetz lautet:
Potenzierst du eine Potenz, lässt du die Basis stehen und multiplizierst die Exponenten.
Was machst du nun also, wenn es beim Potenzieren einer Potenz einen negativen Exponenten gibt?
Um Potenzen mit negativer Hochzahl zu potenzieren, nimmst du die Exponenten mal und benutzt die Vorzeichenregel. Dann ist das Produkt, also die neue Hochzahl auch negativ. Die Basis bleibt gleich.
Beispiel: (24)-3= 2 4·(-3) = 2-12 = 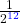
Ist der Exponent – 1, bedeutet das: Das Ergebnis ist der Kehrwert der Zahl. Beispiel: 3-1 = 1/3.
Potenzgesetze Aufgaben
Du willst dein Wissen über die Potenzen und Potenzregeln überprüfen? Hier haben wir verschiedene Aufgaben zu den Potenzgesetzen für dich vorbereitet! Schau direkt vorbei!

