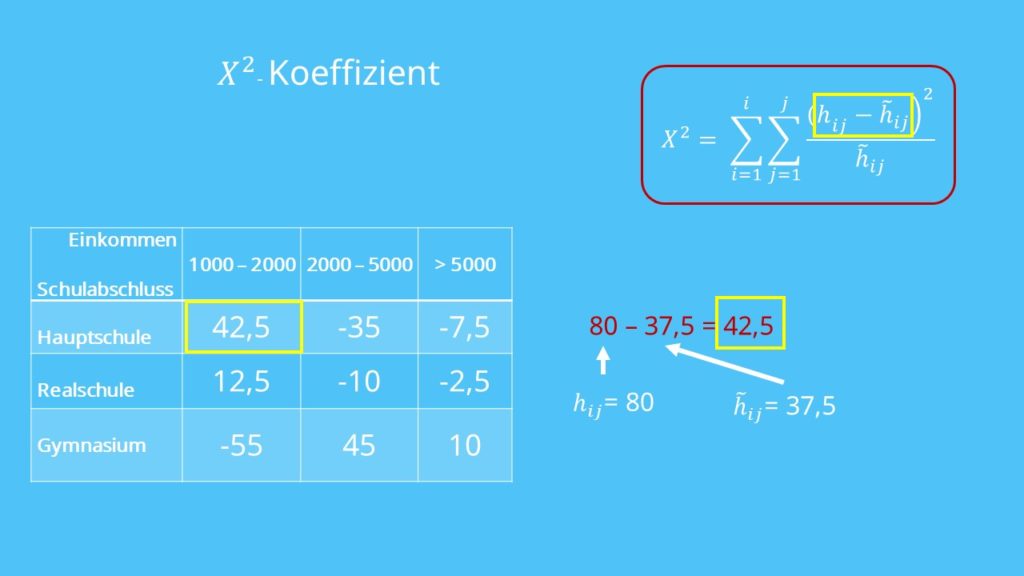
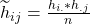Chi Quadrat Koeffizient
Hier wird dir alles zum Chi Quadrat Koeffizient erklärt. Du willst unbedingt herausfinden, wie groß der Zusammenhang zweier Variablen ist? Dann freu dich auf den Chi Quadrat Koeffizient!
Noch leichter geht Lernen nicht; Sieh dir unser Video an und lass dir alles von der Berechnung bis zur Interpretation erklären!
Inhaltsübersicht
Chi Quadrat Koeffizient einfach erklärt
Der Chi Quadrat Koeffizient beschreibt den Zusammenhang zwischen zwei verschiedenen Variablen beliebiger Skalenniveaus . Der Koeffizient ermöglicht den Vergleich von beobachteten Häufigkeiten mit theoretisch zu erwartenden Häufigkeiten, falls Unabhängigkeit vorliegt.
Um den Chi Quadrat Koeffizienten zu verstehen, solltest du dich bereits mit der Kontingenztabelle und der Berechnung von Unabhängigkeiten auskennen. Das haben wir bereits ausführlich in einem eigenen Video erklärt.
Chi Quadrat Koeffizient Beispiel
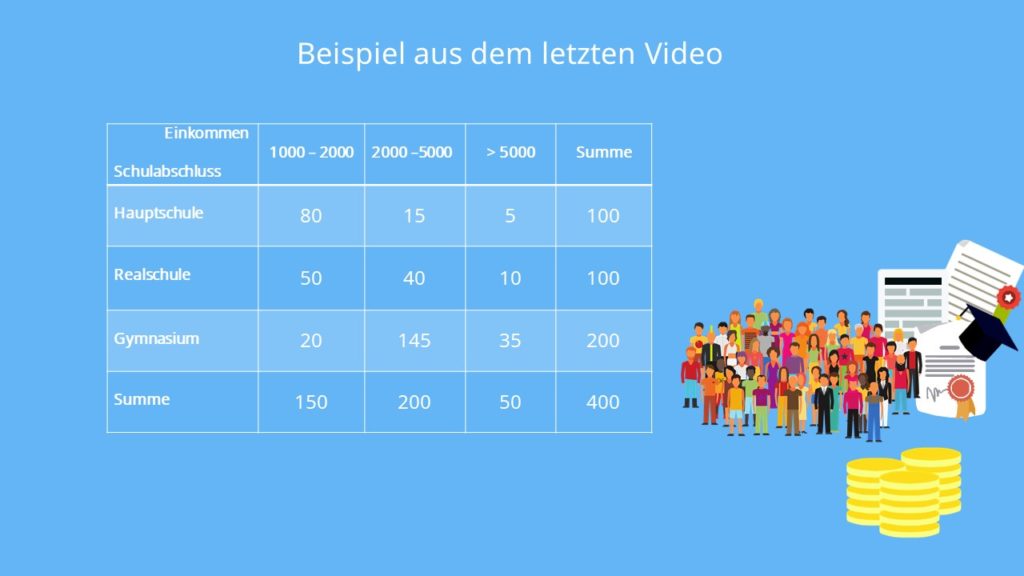
Also berechnen wir doch mal die erwarteten Häufigkeiten für unsere Beispieltabelle aus dem Video Kontingenztabelle. Zur besseren Übersicht stellen wir die Ergebnisse ebenfalls in einer Tabelle dar:
Nun multiplizieren wir die Randhäufigkeiten 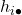 und
und 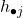 und teilen sie durch n, in diesem Fall durch 400. So erhalten wir die erwarteten Häufigkeiten.
und teilen sie durch n, in diesem Fall durch 400. So erhalten wir die erwarteten Häufigkeiten.
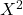 -Koeffizient Formel
-Koeffizient Formel
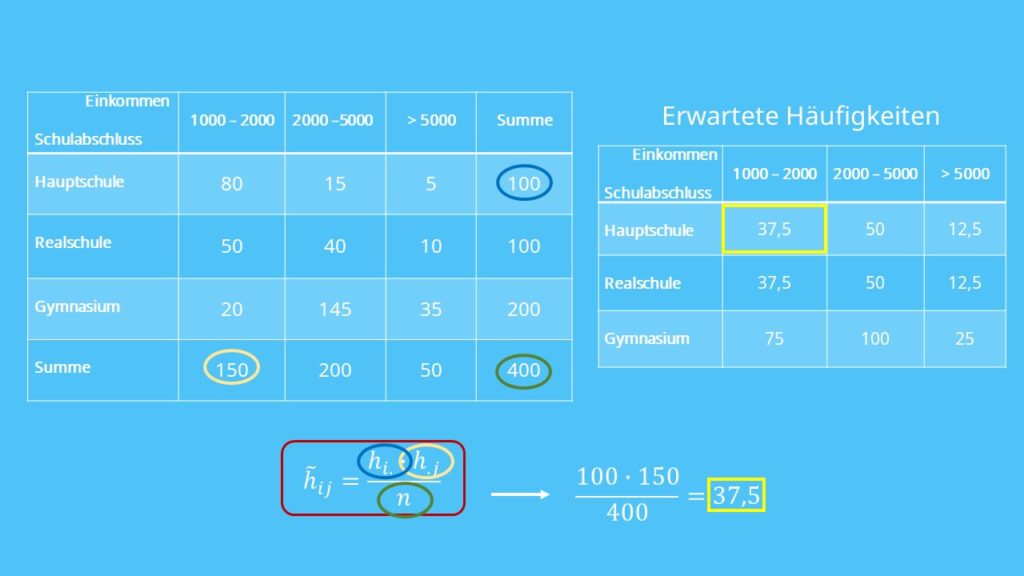
Sehr gut! Jetzt können wir auch schon den Koeffizienten mit dieser Formel berechnen.
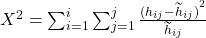
Keine Sorge, du musst nicht alles auf einmal verstehen. Wir werden die Berechnung Schritt für Schritt durchführen.
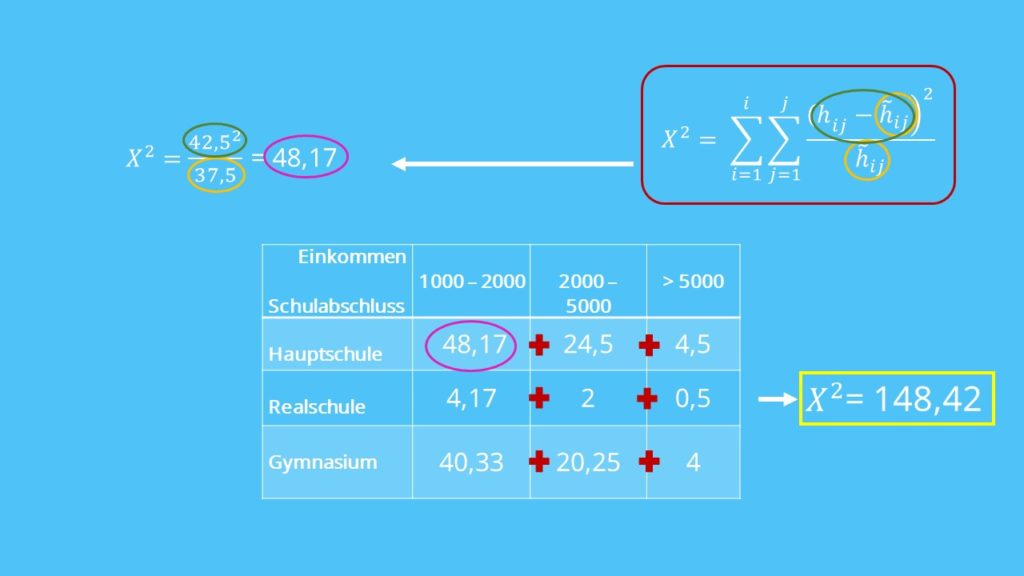
Zuerst ziehen wir die erwarteten Häufigkeiten von den tatsächlichen Häufigkeiten ab. Für die erste Zelle rechnest du also 80 minus 37.5 ist gleich 42.5.
Das machst du jetzt mit allen anderen Zellen auch. Wenn du dich nicht verrechnest, kommst du auf diese Ergebnisse:
Anschließend quadrierst du jede Zelle und teilst sie durch ihre theoretischen Häufigkeiten:
Puh, ganz schön viel Gerechne, oder? Aber du bist schon so gut wie fertig. Du musst nur noch alle Zellen summieren und erhältst dann einen Chi Quadrat Koeffizienten von 148,42.
Chi Quadrat Koeffizient Interpretation
Aber wie können wir so ein hohes Ergebnis nun interpretieren? Genau da liegt das Problem! Der Wertebereich des Koeffizienten liegt nämlich zwischen eins und unendlich und wir können nicht unterscheiden, ob der Wert aufgrund von einer sehr hohen Abhängigkeit oder eines großen n’s entsteht.
Die Aussagekraft reduziert sich also darauf, ob unsere Variablen entweder unabhängig (X2 = 0) oder abhängig
(X2 > 2) sind. In unserem Beispiel liegt folglich Abhängigkeit vor.
Du merkst wahrscheinlich selbst, dass der Chi Quadrat Koeffizient nicht das beste Tool ist, um den Zusammenhang zweier Variablen zu bestimmen. Trotzdem solltest du seine Berechnung beherrschen, denn er ist die Grundlage für den Kontingenzkoeffizienten .
Solange du die Formel also immer Schritt für Schritt berechnest, sollte die Berechnung kein Problem sein.
Glückwunsch! Jetzt weißt du alles Wichtige zum Chi Quadrat Koeffizient und hast damit ein weiteres Zusammenhangsmaß der deskriptiven Statistik kennengelernt.