Harmonisches Mittel
Dieser Beitrag befasst sich mit dem harmonischen Mittel der Statisik, mit welchem sich Mittelwerte von Verhältniszahlen berechnen lassen.
Zu viel Text? Unser Video zur Anwendung des harmonischen Mittels verdeutlicht anhand eines einfachen Beispiels wie du das harmonische Mittel berechen kannst und wo der Unterschied zum gewichteten arithmetischen Mittel liegt.
Inhaltsübersicht
Harmonisches einfach erklärt
Das harmonische Mittel ist ein Lageparameter der Statistik und kommt bei Verhältniszahlen zur Anwendung. Man berechnet mit ihm den Mittelwert der Menge dieser Zahlen. Als Verhältniszahlen werden Brüche bezeichnet, die eine Beziehung widerspiegeln. Also zum Beispiel Studenten pro Einwohner oder Preis pro Quadratmeter.
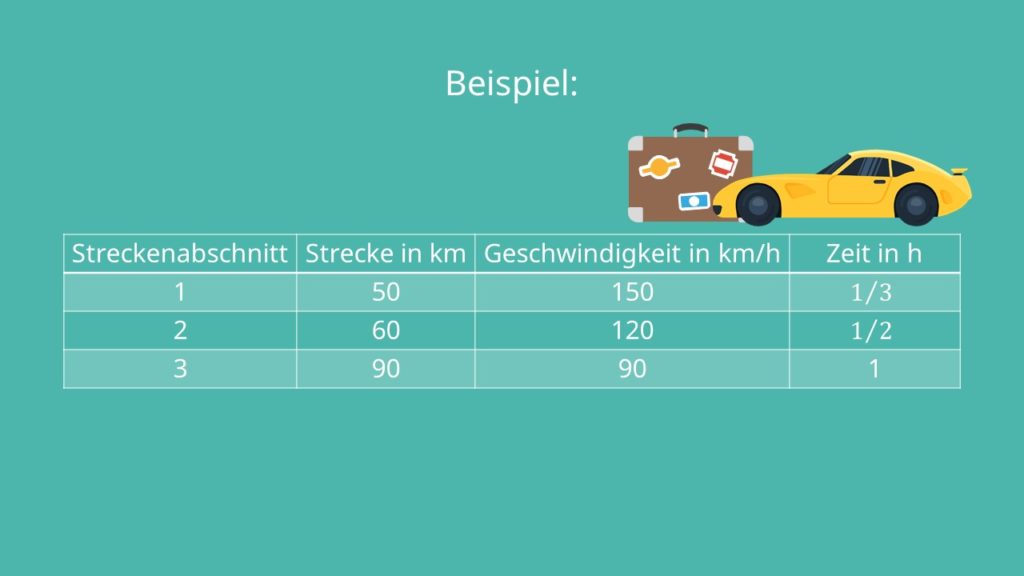
Harmonisches Mittel Beispiel
Angenommen du machst einen Wochenendausflug und fährst eine dreiteilige Strecke. Der erste Streckenabschnitt ist 50 km lang und du fährst 150 km/h. Der zweite Streckenabschnitt ist 60 km lang und der dritte 90 km. Auf den letzten beiden Strecken fährst du 120km/h bzw. 90 km/h.
Harmonisches Mittel Anwendung
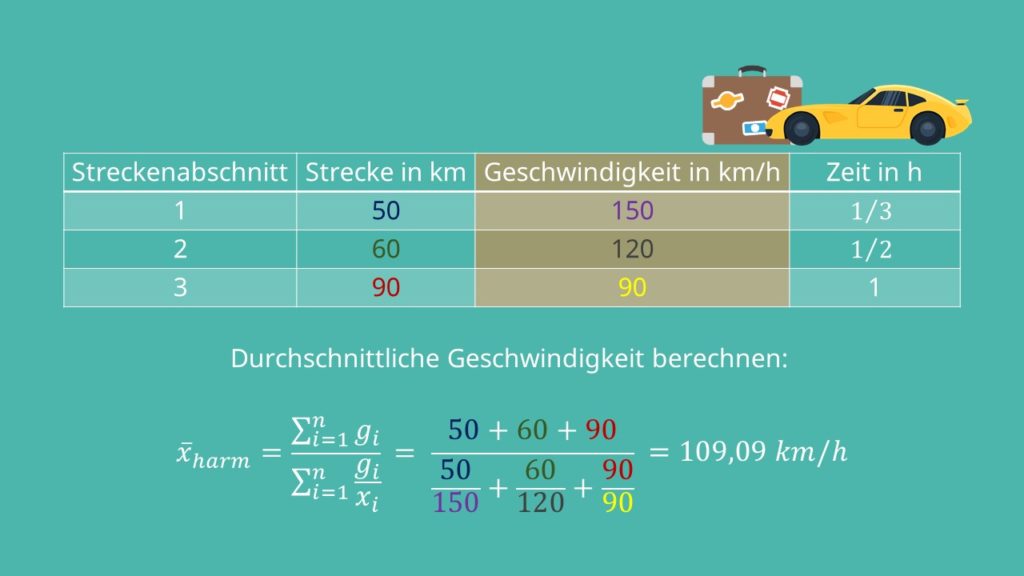
Um die Durchschnittsgeschwindigkeit zu berechnen müssen wir unsere Formel von oben leicht abwandeln:
Du teilst also die Summe der Länge der Teilstrecke durch die Summe der Quotienten aus der Teilstrecke und der Geschwindigkeit der Teilstrecke. In unserem Beispiel rechnen wir also 50 plus 60 plus 90 geteilt durch 50 durch 150 plus 60 durch 120 plus 90 durch 90. Als Ergebnis erhalten wir eine Durchschnittsgeschwindigkeit von 109,09 km/h.
Harmonisches Mittel arithmetisches Mittel Unterschied
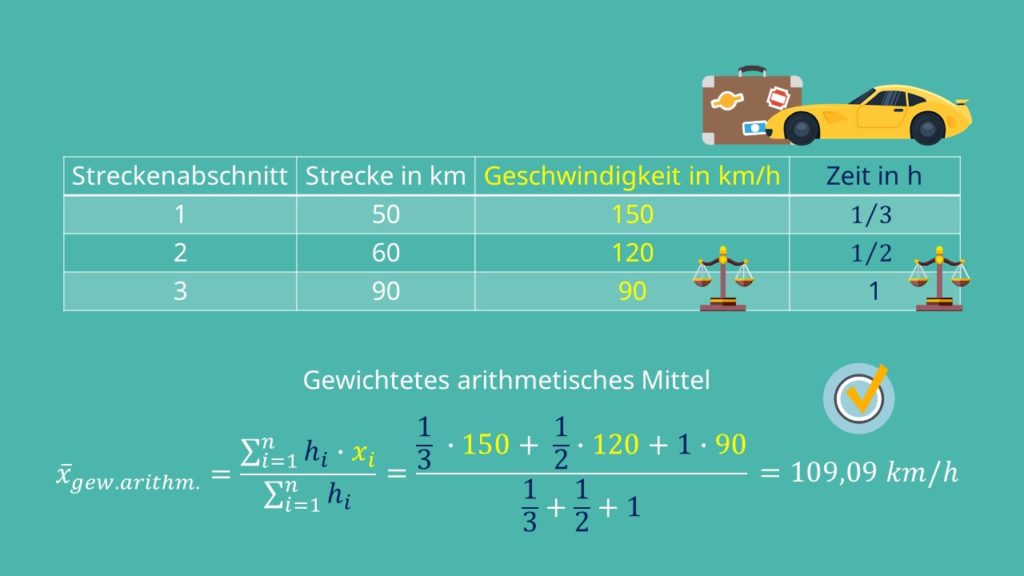
Wenn du die Durchschnittsgeschwindigkeit mit dem normalen arithmetischen Mittel berechnest, würdest du eine falsche Lösung erhalten, weil du nicht berücksichtigst, dass du die verschiedenen Geschwindigkeiten ja unterschiedlich lange fährst. Es gibt aber einen Trick wie du auch mit dem arithmetischen Mittel auf die richtige Lösung kommst und zwar indem du die Geschwindigkeiten mit den Zeiten gewichtest. Die Formel dazu sieht so aus:
Hi steht dabei für die Zeit, die du brauchst um den jeweiligen Streckenabschnitt zurückzulegen und xi steht wieder für die Geschwindigkeit. In unserem Beispiel würde die Rechnung also so aussehen:
Wie du siehst, kannst du also auch mit dem gewichteten arithmetischen Mittel auf das richtige Ergebnis kommen!
Jetzt weißt du wie du das harmonische Mittel berechnest und dass du mit dem gewichteten arithmetischen Mittel auf dasselbe Ergebnis kommst!