Standardabweichung
Du möchtest verstehen, was die Standardabweichung ist und wie du sie berechnest? Hier im Beitrag erklären wir dir alles Wichtige dazu!
Inhaltsübersicht
Standardabweichung — einfach erklärt
Die Standardabweichung ist ein Maß dafür, wie sehr Werte von ihrem eigenen Durchschnittswert abweichen. Den Durchschnittswert nennst du auch Mittelwert.
Beispiel:
Sechs Schüler haben die Noten aus einer Mathe-Klausur bekommen. Die Verteilung der Noten sieht so aus:
| Note xi | 1 | 2 | 3 | 4 | 5 |
| Anzahl | 1 | 2 | 2 | 1 | 0 |
Um die Standardabweichung zu berechnen, brauchst du zuerst den Mittelwert  aller Noten:
aller Noten:
![Rendered by QuickLaTeX.com \[\textcolor{red}{\mu}= {\frac{(\textcolor{olive}{1} \cdot \textcolor{blue}{1}) + (\textcolor{olive}{2} \cdot \textcolor{blue}{2}) + (\textcolor{olive}{3} \cdot \textcolor{blue}{2}) + (\textcolor{olive}{4} \cdot \textcolor{blue}{1}) + (\textcolor{olive}{5} \cdot \textcolor{blue}{0})}{6}} = \frac{1+4 + 6 + 4}{6} = \frac{15}{6} = \textcolor{red}{2,5}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-6ff173b5d4e9359962b09e7ee8e0ffaa_l3.png)
Als Nächstes musst du die Häufigkeit pi von jeder Note berechnen:
![Rendered by QuickLaTeX.com \[p_1=\frac{\textcolor{blue}{1}}{6}\quad\quad p_2=\frac{\textcolor{blue}{2}}{6}\quad\quad p_3=\frac{\textcolor{blue}{2}}{6}\quad\quad p_4=\frac{\textcolor{blue}{1}}{6}\quad\quad p_5=\frac{\textcolor{blue}{0}}{6}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-50cb927c54d5833e27076ae7c73d3a06_l3.png)
Nun kannst du die Standardabweichung 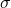 mit der Formel berechnen:
mit der Formel berechnen:
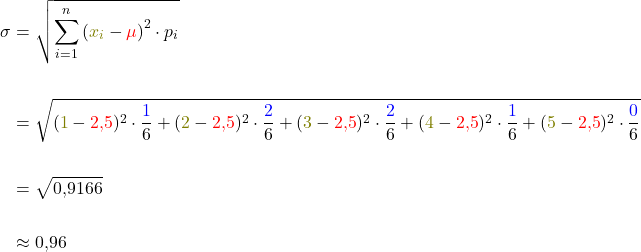
Eine Standardabweichung von etwa 0,96 bedeutet in diesem Fall, dass die Noten der Schüler relativ nah am Mittelwert liegen.
Standardabweichung Formel
Für die Berechnung brauchst du die Formel der Standardabweichung. Die Formel sieht so aus:
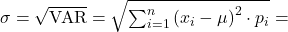
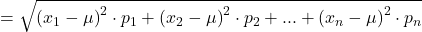
-
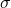 ist das Abkürzung für die Standardabweichung (der Grundgesamtheit)
ist das Abkürzung für die Standardabweichung (der Grundgesamtheit) -
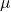 ist der Mittelwert, bzw. Erwartungswert
ist der Mittelwert, bzw. Erwartungswert
-
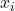 ist das einzelne Ergebnis des Zufallsexperiments
ist das einzelne Ergebnis des Zufallsexperiments
-
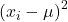 ist die quadratische Abweichung
ist die quadratische Abweichung
-
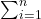 beschreibt, dass eine Summe der quadrierten Abweichungen vom Mittelwert berechnet wird
beschreibt, dass eine Summe der quadrierten Abweichungen vom Mittelwert berechnet wird -
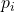 ist der Gewichtungsfaktor
ist der Gewichtungsfaktor
Die Standardabweichung ist also die Wurzel der Varianz.
Standardabweichung berechnen
Die Standard abweichung kannst du mit der Formel in vier Schritten berechnen:
- Den Mittelwert berechnen
- Die Wahrscheinlichkeiten berechnen
- Die Werte in die Formel einsetzen
- Die Formel ausrechnen
Das gehen wir jetzt Schritt für Schritt durch.
Schritt 1: Den Mittelwert berechnen
Um den Mittelwert
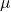 zu berechnen, addierst du zuerst alle deine Werte. Dann teilst du die Summe durch die Anzahl der Werte.
zu berechnen, addierst du zuerst alle deine Werte. Dann teilst du die Summe durch die Anzahl der Werte.
Für das Beispiel der fünf Schüler brauchst du den Mittelwert aller Noten.
| Note | 1 | 2 | 3 | 4 | 5 |
| Anzahl | 0 | 2 | 2 | 1 | 0 |
Es gibt zweimal die Note 2, zweimal die 3 und einmal die 4. Insgesamt gibt es fünf Noten. Also berechnest du den Mittelwert so:
![Rendered by QuickLaTeX.com \[\textcolor{red}{\mu} = {\frac{(\textcolor{olive}{1} \cdot \textcolor{blue}{0}) + (\textcolor{olive}{2} \cdot \textcolor{blue}{2}) + (\textcolor{olive}{3} \cdot \textcolor{blue}{2}) + (\textcolor{olive}{4} \cdot \textcolor{blue}{1}) + (\textcolor{olive}{5} \cdot \textcolor{blue}{0})}{5}} = \frac{4 + 6 + 4}{5} = \frac{14}{5} = \textcolor{red}{2,8}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-674f39b4d640fb91943d2daa0f7d744c_l3.png)
Schritt 2: Die Wahrscheinlichkeiten berechnen
Der nächste Schritt ist die Berechnung der relativen Häufigkeit pi für jede Note. Das zeigt dir, wie jeder Wert im Vergleich zur Gesamtanzahl der Werte gewichtet wird.
Im Beispiel sieht das so aus:
- Für Note 1:
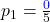
- Für Note 2:
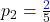
- Für Note 3:
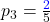
- Für Note 4:
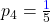
- Für Note 5:
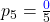
Wenn alle Ereignisse gleich wahrscheinlich sind, kannst du statt mit pi zu multiplizieren auch durch die Gesammtzahl n teilen.
![Rendered by QuickLaTeX.com \[\frac{(x_i - \mu)^2}{n}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-1150bb2dc18bae13e629f77bd700797a_l3.png)
Schritt 3: Setze alle Werte in die Formel ein
Nun setzt du alle Werte in die Formel für die Standardabweichung ein.
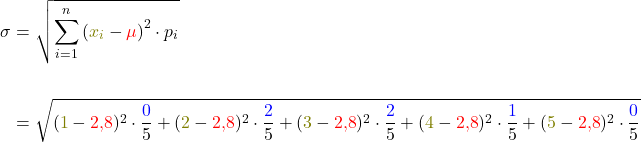
Wichtig: Die Formel der Standardabweichung kannst du auf zwei Weisen aufschreiben: Eine Möglichkeit ist es, wie wir es machen: Du multiplizierst die quadrierten Differenzen mit ihrem jeweiligen Gewichtungsfaktor pi, wie 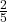 oder
oder 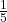 .
.
Die zweite Variante ist es, die quadrierten Differenzen zuerst mit der Anzahl der Noten zu multiplizieren. Anschließend teilst du durch die Gesamtzahl aller Noten.
Schritt 4: Die Formel ausrechnen
Als Letztes musst du die Formel ausrechnen. Dazu berechnest du als Erstes die Differenzen und quadrierst sie.
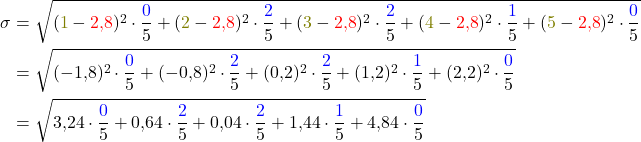
Dann multiplizierst du jeweils die relativen Häufigkeiten.
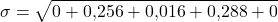
Zum Schluss addierst du alles und ziehst die Wurzel.
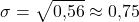
Ergebnis der Standardabweichung
Doch was sagt das Ergebnis jetzt aus? Hier sind einige Schlüsselpunkte zur Interpretation:
-
Niedrige Standardabweichung: Wenn die Standardabweichung klein ist, bedeutet das, dass die meisten Datenpunkte nah am Mittelwert liegen. Bei unserem Noten-Beispiel: Je kleiner die Standardabweichung, desto ähnlicher sind die Noten.
-
Hohe Standardabweichung: Eine hohe Standardabweichung zeigt an, dass die Daten weit um den Mittelwert verstreut sind. Das bedeutet, es gibt eine große Variabilität und die Werte können sehr unterschiedlich sein. Es gibt zum Beispiel viele Einser und viele Fünfer.
-
Null: Wenn die Standardabweichung null ist, haben alle Datenpunkte den gleichen Wert — sie sind also identisch. Zum Beispiel haben alle Schüler die Note 3.
Für die Berechnung einer Stichprobe  lautet die Formel der Standardabweichung:
lautet die Formel der Standardabweichung:
![Rendered by QuickLaTeX.com \[s = \sqrt{\frac{1}{n-1} \sum_{i=1}^{n} (x_i - \mu)^2}\]](https://d1g9li960vagp7.cloudfront.net/wp-content/ql-cache/quicklatex.com-2c6b0002dda90d841d6f02fb27bbbf21_l3.png)
-
 ist das Kürzel für die Standardabweichung der Stichprobe
ist das Kürzel für die Standardabweichung der Stichprobe -
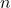 ist die Anzahl der Beobachtungen in der Stichprobe
ist die Anzahl der Beobachtungen in der Stichprobe -
 steht für die Anpassung der Freiheitsgrade in der Formel, um eine genauere Schätzung der Populationsstreuung zu gewährleisten, indem es eine Überbewertung der Stichprobenvarianz verhindert
steht für die Anpassung der Freiheitsgrade in der Formel, um eine genauere Schätzung der Populationsstreuung zu gewährleisten, indem es eine Überbewertung der Stichprobenvarianz verhindert
Standardabweichung — häufigste Fragen
-
Was genau ist die Standardabweichung?
Die Standardabweichung ist ein statistisches Maß, das angibt, wie weit Werte in einem Datensatz im Durchschnitt vom Mittelwert (dem Durchschnittswert) entfernt liegen. Sie zeigt die Streuung oder Variabilität der Werte um diesen Mittelwert herum an.
-
Wie rechnet man die Standardabweichung aus?
Du berechnest die Standardabweichung, indem du die Summe der quadrierten Abweichungen aller Messwerte vom Mittelwert mit der relativen Häufigkeit der Messwerte gewichtest und vom Ergebnis die Wurzel ziehst.
-
Was ist das Symbol der Standardabweichung?
Das Symbol für die Standardabweichung ist der griechische Buchstabe Sigma (σ). Für die Standardabweichung einer Stichprobe ist es s.
Standardabweichung Excel
Jetzt weißt du, was die Standardabweichung ist und wie du sie berechnest. Möchtest du auch lernen, wie du die Standardabweichung ganz einfach mit Excel berechnen kannst? Hier zeigen wir dir Schritt für Schritt zeigt, wie das geht.
